PROGRAM 50

                                            C++                                           

       K. Dzwonkiewicz                                     

 

The Monte Carlo Method

Monte Carlo methods are computer models that involve some chance or probabilistic behavior.  (Monte Carlo is the famous gambling resort in Monaco.)

            Suppose we have a figure on the x-y plane and we want to estimate its area.  In previous programs we used inscribed or circumscribed rectangles or trapezoids.  The Monte Carlo method also finds area but by using probability and ratio or percent.

 

Consider the following figure…   

                                                           

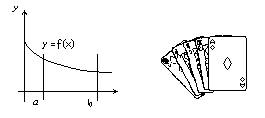
Suppose the figure lies within some known rectangle.  The area of interest lies between two x values           a £ x £ b.  For any random x value within the area of consideration, we will match a random y value also within the rectangle, the point will fall either above the curve or on it or below.

 

If we choose an interval… a £ x £ b and also, 0 £ y £ f(a) (see figure above).  The bounded area below the curve is called the definite integral of the function f(x) on the interval [a,b]

 

The Monte Carlo method is to throw many random points uniformly distributed over the rectangle that contains our area of interest.  Some points will land inside the figure and some will land outside.  The fraction of all points that land inside should be approximately equal to the ratio of the figure to the area of the rectangle.

 

Randomize 10,000 points counting how many are on or below the curve.  Multiply the ratio of on and below divided by 10000.0 (or use percent) times the area of the rectangle.  This will give an approximation of the area under the curve for the interval considered.

 

HINTS: We must get a floating-point number for our random.  This of course can be done by asking interval start and end, then put a multiple ( by 100) inside the random.  Once you get the random value divide by 100 and use this value for x (same process for y)

            cin>>startval;  // 0 is input

            cin>>endval;   // 10 is input

                        x=(random (endval*100-startval*100)+startval)/10.0;  // better check this!

            (This will generate decimals within 0.00-10.00)

The area of the rectangle will be the highest point on the curve times the width (to get the max value of f(x); find the first derivative… set it to zero and solve for the needed x value that when put into the original expression will result in rectangle height)

Use the equation… f(x)= -x² +10x +24, restrict your x values to be in range [0,10].

Approximate area is… 406.666666666666