Example 2.1
How many cycles are there?
Solution
The answer is 2 cycles.
The saw tooth wave at C goes negative first but that doesn't change the number of cycles or the definition of a cycle.

Figure 1 showing 4 different wave forms. A. is a sine wave, B, is a triangular wave, C. is a sawtooth wave which slopes up to the right before returning quickly to a negative voltage, and D. is a square wave.

T = 1 / 60 = 0.0167 = 1.67 x 10^-2 (1.67e-2)

BACK

Example 2.3

It is possible, and done all the time, to measure the period of a wave using an oscilloscope. Such a measurement gives a period of 4.0 milliseconds. What is the frequency of this wave?

Solution

f = 1 / T

Worked without using scientific notation.

f = 1 / .004 seconds

f = 250 cycles

I'm not going to humor you very long about learning scientific notation. Eventually you're going to have to go back to the end of the DC chapter and learn it. You can do it now or do it later; but eventually you will do it.

Worked using scientific notation.

f = 1 / 4 x 10^-3 = 250 cycles = 2.50 x 10² = (2.50e2)

Scientific notation or not, most people would just say 250 cycles.

BACK

Example 2.4

If a 40 microfarad capacitor is discharged from 150 volts to 120 volts in 16 milliseconds, what is the current?

Solution

Given:
Delta V = 150 - 120 = 30 volts.
Delta t = 16 milliseconds = 16 x 10^-3 (16e-3)
It's alright to break the rules once in a while. I won't tell if you won't.
C = 40 x 10^-6 (40e-6)

I = 40 x 10^-6 x 30 / 16 x 10^-3 = 7.5 x 10^-2 = (7.5e-2)

BACK

Example 2.5

What size capacitor should be used in a full wave power supply if the peak to peak ripple is to be no more than 10 volts and the load current is 100 mA? Full wave power supply means that the discharge time for the capacitor is approximately 8 milliseconds. (The full wave rectifier gives a ripple frequency of twice the line frequency which would be 120 cycles. The period is 8.333 milliseconds. The capacitor charges for a very short time and discharges for most of the cycle.) The peak to peak ripple is how much the capacitor charges up and then discharges. The load current of 100 mA will discharge the capacitor by 10 volts in 8 milliseconds. Enough hints; work the problem already.

Solution

Given:
Delta V = 10 volts,
Delta t = 8 milliseconds = 8 x 10^-3 seconds,
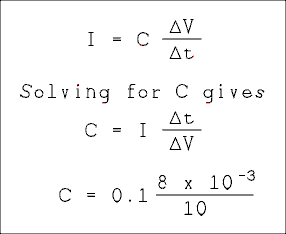
I = 100 mA = 0.1 A. I = C delta v over delta t. Solving for I gives. C = I delta t over delta v. C = 0.1 amps times 8 times 10 to the minus 3 seconds over 10 volts.

I = C delta v over delta t. Solving for I gives. C = I delta t over delta v. C = 0.1 amps times 8 times 10 to the minus 3 seconds over 10 volts.

C = 8 x 10^-5 = (8e-5) farads.
C = 80 microfarads.

BACK

Example 2.6

What is the reactance of a 0.01 microfarad capacitor at 20 cycles?

Solution

X_C = 1/(2 pi f C)
X_C = 1/(2 pi 20 x .01 x 10^-6)
X_C = 7.96 x 10⁵ = (7.96e5) ohms

BACK

Example 2.7

If a 40 microfarad capacitor is connected across the 120 volt 60 cycle power line, how much current will flow? How much power will be dissipated?

Solution

First we calculate X_C.

X_C = 1/(2 pi f C)
X_C = 1/(2 pi 60 x 40 x 10^-6)
X_C = 6.63 x 10¹ = 66.3 ohms.

Now we use the AC version of ohm's law to calculate the current.

I = V / X_C
I = 120 volts / 66.3 ohms = 1.81 amps.

To actually calculate the power we would need to know the dissipation factor of the capacitor. Since we don't know that all we can say is that the power is ZERO!

BACK

Example 2.8

What is the reactance of a 300 microhenry inductor at a frequency of 455 kc?

Solution

X_L = 2 pi f L
X_L = 2 pi 455 x 10³ x 300 x 10^-6
X_L = 8.58 x 10² = (8.58e2) = 858 ohms.

BACK

Example 2.9

A 0.01 microfarad capacitor and a 15900 ohm resistor are connected to form a high pass filter. What is the attenuation ratio (Ar) at frequencies of; (a) 10 cycles, (b) 100 cycles, (c) 1000 cycles, and (d) 10 kc?

Solution

R = 15900 ohms, given.
(a)
X_C = 1 / (2 pi f C)
X_C = 1 / (2 pi 10 x 0.01 x 10^-6)
X_C = 1.59 x 10⁶ = (1.59e6) Ohms.

Ar = R / Square root of (R² + Xc²)
Ar = 1.59 x 10⁴ / Square root of ([1.59 x 10⁴]² + [1.59 x 10⁶]²)
Ar = 1.59 x 10⁴ / Square root of (2.53 x 10⁸ + 2.53 x 10¹²)
Ar = 1.59 x 10⁴ / Square root of (0.000253 x 10¹² + 2.53 x 10¹²)

When 0.000253 is added to 2.53 it gives 2.53253 and then when it is rounded off to 3 digits it gives 2.53. So we have,

Ar = 1.59 x 10⁴ / Square root of (2.53 x 10¹²)
Ar = 1.59 x 10⁴ / 1.59 x 10⁶
Ar = 1.00 x 10^-2

(b)

X_C = 1 / (2 pi f C)
X_C = 1.59 x 10⁵ = (1.59e5) Ohms.

Ar = R / Square root of (R² + Xc²)
Ar = 1.59 x 10⁴ / Square root of ([1.59 x 10⁴]² + [1.59 x 10⁵]²)
Ar = 1.59 x 10⁴ / Square root of (2.53 x 10⁸ + 2.53 x 10¹⁰)
Ar = 1.59 x 10⁴ / Square root of (0.0253 x 10¹⁰ + 2.53 x 10¹⁰)

When 0.0253 is added to 2.53 it gives 2.5553 and then when it is rounded off to 3 digits it gives 2.56. So we have,

Ar = 1.59 x 10⁴ / Square root of (2.56 x 10¹⁰)
Ar = 1.59 x 10⁴ / 1.60 x 10⁵
Ar = 0.994 x 10^-1 = 9.94 x 10^-2 = (9.94e-2)

Pretty close to 1/10.

(c)

X_C = 1 / (2 pi f C)
X_C = 1.59 x 10⁴ = (1.59e4) Ohms.

Ar = R / Square root of (R² + Xc²)
Ar = 1.59 x 10⁴ / Square root of ([1.59 x 10⁴]² + [1.59 x 10⁴]²)
Ar = 1.59 x 10⁴ / Square root of (2.53 x 10⁸ + 2.53 x 10⁸)

When 2.53 is added to 2.53 it gives 5.06. So we have,

Ar = 1.59 x 10⁴ / Square root of (5.06 x 10⁸)
Ar = 1.59 x 10⁴ / 2.25 x 10⁴
Ar = 0.707 = 7.07 x 10^-1

(d)
X_C = 1 / (2 pi f C)
X_C = 1.59 x 10³ = (1.59e3) Ohms.

Ar = R / Square root of (R² + Xc²)
Ar = 1.59 x 10⁴ / Square root of ([1.59 x 10⁴]² + [1.59 x 10³]²)
Ar = 1.59 x 10⁴ / Square root of (2.53 x 10⁸ + 2.53 x 10⁶)
Ar = 1.59 x 10⁴ / Square root of (2.53 x 10⁸ + 0.0253 x 10⁸)

When 2.53 is added to 0.0253 it gives 2.5553. When it is rounded off it gives 2.56. So we have,

Ar = 1.59 x 10⁴ / Square root of (2.56 x 10⁸)
Ar = 1.59 x 10⁴ / 1.60 x 10⁴
Ar = 0.994 = 9.94 x 10^-1

Getting real close to 1.00.

BACK

Example 2.10

A 0.1 microfarad capacitor and a 15900 ohm resistor are connected as a low pass filter. Calculate the attenuation ratio (Ar) at frequencies of; (a) 10 cycles, (b) 100 cycles, (c) 1000 cycles, and (d) 10 kc.

Solution

Details will be shown for only one calculation. After that results will be summarized.

(a)

X_C = 1 / (2 pi f C)
X_C = 1 / (2 pi 10 x 0.1 x 10^-6)
X_C = 1.59 x 10⁵

Ar = X_C / Square root of (R² + X_C²)
Ar = 1.59 x 10⁵ / Square root of ([1.59 x 10⁴]² + [1.59 x 10⁵]²)
Ar = 1.59 x 10⁵ / Square root of (2.53 x 10⁸ + 2.53 x 10¹⁰)
Ar = 1.59 x 10⁵ / Square root of (0.0253 x 10¹⁰ + 2.53 x 10¹⁰)
Ar = 1.59 x 10⁵ / Square root of (2.56 x 10¹⁰)
Ar = 1.59 x 10⁵ / 1.60 x 10⁵
Ar = 9.94 x 10^-1 = (9.94e-1)