TD n°1: Les théories de l’esprit

A) D’ou vient l’intérêt pour les théories de l’esprit?

- Piaget (p.15)

- Métacognition dans les années 1970: ce courant est né de l’idée que notre fonctionnement cognitif repose sur l’utilisation de stratégies et ces dernières dépendant de nos connaissances sur notre propre fonctionnement mental = nos connaissances sur nos connaissances

Théories de l’esprit (Anne-Marie Mellot): étudier les connaissances et les représentation que l’enfant a à un moment donné de son développement à l’égard du fonctionnement cognitif et plus généralement à l’égard du fonctionnement général de l’être humain.

Théories de l’esprit: capacité d’attribuer des états mentaux (émotions, pensées, désirs, etc.) à soi-même et à autrui.

B) Trois questionnement principaux:

1 - Comment ces théories s’acquièrent et comment elles se développent?

Il existe une séquence développementale présente dans les différents domaines du développement.

Quand l’enfant est capable de faire semblant (accès à la fonction symbolique), il dispose des représentations mentales des objets dissociées des objets réels ( cela ne signifie pas qu’il en est conscient).

À trois ans, l’enfant fait une distinction claire entre les représentations mentales et l’objets physique (il est conscient).

Trois critères de distinctions entre représentation mentale et objet physique (mellot):

- évidence des sens
- évidence publique (l’autre voit objet pas rep.)
- existence permanente (des objet pas des rep.)

Production langagière:
- 2-3 ans: penser et savoir
- 5-6 ans: deviner

Perception
- 3-4 ans: sait si l’autre voit ou non ce qu’il voit (attribution d’ignorance)
- 4-5 ans: peut prédire ce que l’autre voit

Distinction apparence - réalité:
à 4 ans, réussite à l’épreuve du caillou éponge.

Origine des savoirs:

- 4-5 ans: enfant fait le lien entre accès perceptif et le savoir relatif à l’objet (il comprend que la vision est un outil à la connaissance du monde)
- Inférence pas possible avant 6 mois.

2 - Dans quelles  mesures ces connaissances sont-elles intégrées dans un ensemble cohérent (système cohérent= théorie)?

- Wellman (1988): il y aurait un changement de théorie vers 4-5 ans:

Avant 4-5 ans, l’enfant conçoit l’esprit humain comme un réservoir d’états mentaux. Ces états mentaux viendraient directement de la réalité (le savoir vient de la réalité.

Après 4-5 ans, l’enfant concevrait l’esprit humain comme générateur (médiateur) d’états mentaux: il conçoit, interprète, traite et transforme l’information.

3 - Comment les enfants font-ils appel à ces connaissances pour expliquer et prédire les conduites humaines?

-> Paradigme de fausses croyances (p.5)

Le premier principe à acquérir par l’enfant: le comportement d’autrui est représenté par la conception mentale des choses de cet individu.

Le paradigme de fausses croyances:

Question 1: Prendre connaissance du protocole

Question 2: quel est l’objectif de chacune des questions?

QP: Te souviens-tu du nom des deux amis? Nous allons voir des photos. Tu diras si c’est Pinocchio ou Lapin blanc qui est sur la photo. Qui est-ce, que fait-il?  Maintenant, nous allons voir si tu te souviens bien de ce qu’il y a dans la cuisine de Pinocchio et de Lapin Blanc. Montre-moi où est la table avec le tiroir, où est le frigidaire, où est le placard?
-> Les questions préalables cherchent à savoir si l’enfant comprend et maîtrise les termes langagiers employés et à familiariser l’enfant à la situation.

Q1 : Où le lapin blanc va chercher le chocolat?
-> Teste la mémorisation de l’histoire et la compréhension générale de la structure de base de la scène.

Q2 : Est-ce que LapinBlanc a bien rangé le chocolat? Explique-moi pourquoi?
-> permet de s’assurer qu’il voit la différence et d’anticiper la suite de l’histoire.

Q3 : Montre-moi où Pinocchio va chercher le chocolat?
=> question centrale qui teste les fausses croyances.
-> Teste si l’enfant fait la différence entre ses représentations et celles de Pinocchio
-> Prédiction du comportement de Pinocchio
-> Enfant doit se décentrer de son point de vue
-> construction de la représentation de l’esprit de Pinocchio.

Q4: Si l’Enfant répond le placard et Q3, alors: comment pinocchio sait-il que le chocolat est dans le placard?
-> = justification de la réponse à la Q3.
-> pour connaître le raisonnement de l’enfant (évite les bonnes réponses au hasard)

Q5: Que se passe-t-il? Pourquoi Pinocchio n’est-il pas content?
-> = justification aux deux questions précédentes + la prédiction de l’émotion et de l’action de Pinocchio.

Q6: Où Pinocchio va-t-il chercher le chocolat maintenant? Pinocchio est-il sûr de trouver le chocolat dans le placard (ou le frigo) ?
-> est-il sûr = sert à s’assurer que l’enfant a compris que pour Pinocchio le chocolat peut être autant dans le placard que dans le frigo.

Question 3 (p7)

Quelles autres questions pourrait-on poser et avec quelles intentions?

-> questions qui conduisent pas à pas à la résolution de la tâche et inciter à la décentration (on l’aide)
 -> est-ce que le chocolat a changé de place depuis le début de l’histoire?
 -> Où se trouve le chocolat après le départ du lapin?

-> Questions qui affinent la discrimination développementale des niveaux de conception (car, dans l’expérience, on retrouve deux niveaux: l’enfant a les mêmes connaissances que le personnage ou en a des différentes).
 -> intermédiaire: avant Q3, demander: est-ce que Pinocchio sait où est le    chocolat? (test attribution d’ignorance -> différent de fausses croyances).
 -> supérieur: est-ce que le lapin sait que Pinocchio ne sait pas où est le    chocolat?

Question 4 (p7): Pouvez-vous prévoir (et selon quelles justifications) les réponses typiques d’enfants âgés de 3, 5 et 7 ans?

3 ans:
- Q1 : Lapin -> tiroir
- Q3 : Pinocchio -> placard

5 ans:
- Q1 : Lapin -> tiroir
- Q3 : Pinocchio -> tiroir ; où alors : placard (pas de test d’hypothèse)

7 ans:
- Q1 : Lapin -> tiroir
- Q3 : Pinocchio -> tiroir; où alors : placard ou frigidaire.

Question 5 (p7): L’expression “fausses croyances” vous paraît-elle justifiée? Pourquoi?

Oui, parce que l’enfant doit attribuer au personnage une croyance qui est fausse par rapport à sa propre représentation et à la réalité.

Conclusion:

- Avant 4 1/2 ans  - 5 ans: l’enfant répond aux questions en se référent à sa propre représentation de la réalité
- Après 5 ans: l’enfant prend en compte l’état mental d’autrui pour prédire l’action d’autrui. Donc, il comprend que l’autre à une représentation différente de la leur et différente de la réalité.
L’enfant attribue plutôt un état d’ignorance que de fausses croyances car c’est plus facile pour lui d’invoquer une fausse croyance pour expliquer une conduite en cours plutôt que de prédire un comportement.

TD n°2: Développement des conduites de catégorisation

- Catégorie:

Conduite adaptative consistant à découper l’environnement physique et social afin de mettre de l’ordre (et de rendre plus simple) dans l’environnement et dans nos connaissances.

- Piaget : 3 stades :
-> 1° : collections figurales (2 à 4 ans)
-> 2° : collection non figurales (4 à 7 ans)
-> 3° : collection logiques (7 ans et +)

- Houdé, 1992 : les représentations schématiques

“ Le schéma est une structure spatialement et / ou temporellement organisée dont les parties sont connectées sur la base de contiguités qui ont été expérimentées dans l’espace et dans le temps”.

-> 2 types de schémas:
 - La contiguité spatiale: situationnelle
 - la contiguité temporelle: événementielle (script -> Nelson)

- généralement pour étudier les catégorisations, les chercheurs utilisent deux types d’épreuves:
 - l’épreuve de tri libre (ce qui va bien ensemble)
 - l’épreuve d’appariemment (ça va bien avec quoi? -> test si les catégories sont   schématiques ou taxonomiques).

Q1 : Quels sont les différents tris possibles que l’in peut effectuer avec ce matériel?

-> Taxonomique: animaux, véhicule, personnage
-> Schématique: plage ou ferme ( = p ou f)
-> Slot filler: animaux (p ou f), personnage (p ou f), véhicule (p ou f)

Q2: Imaginez un exemple de triade:

-> Cible : poisson
-> Schématique : bateau
-> Taxonomique: poule (il faut mettre un animal différent du schéma choisit -ici plage - sinon, on ne peut pas conclure si la catégorisation est schématique ou taxonomique).

Q3 : Faites des hypothèses sur l’effet des différents facteurs manipulés dans cette expérience.

Plan:
S < A3 > * E2

Facteurs:
VI1: âge (A3)
VI2: épreuve (E2)

Variable dépendantes:
VD1: la production spontannée
VD2: l’évaluation de la catégorie taxonomique

Hypothèses:

- S’il existe une hiérarchie entre les catégories taxonomiques et schématiques:
-> Pour la production spontannée: 5 ans = catégorie schématique, 9 ans= taxonomique
-> Pour l’évaluation de la cat. taxo. : augmentation de l’acceptation avec l’âge.

- S’il existe une coexistence entre les catégories taxonomiques et schématiques:
-> Pour la production spontannée: le type de catégories ne changera pas, peu importe l’âge.
-> Pour l’évaluation de la cat. taxo. : pas d’effet d’âge, pas d’effet d’épreuve.

Q4 : Que constatez-vous?

Ces deux types d’épreuves (tri libre et apparemment) n’activent pas les mêmes types de catégories.

Q5 : Quels sont les avantages et les inconvénients de cette analyse en terme de sujets?

Avantage: avoir des information sur les performances au niveau individuel.
Inconvénient:

Q6 : Que constatez-vous?

Avec l’âge, il y a une augmentation de l’acceptation des catégories taxonomiques dans le tri libre et l’appariemment.
Quelque soit l’âge, la majorité d’acceptation en tri libre et la minorité en apparemment
-> résultats en faveur d’une coexistence car dès 5 ans, l’enfant accepte les catégories taxonomiques en tri libre.

Q7 : Quels sont les avantages et les inconvénients de cette analyse en terme de sujet?

Avantages:
Inconvénients: néglige les différences individuelles.

Q8 : À votre avis quels sont les types de justifications que l’on peut estimer correctes?

Accepte: terme catégoriel, énonciation de sous-catégories, propriétés définitoires
Refuse: propriétés non définitoire, désignation des dessins, explication d’un lien fonctionnel.

Q9 : Que constatez-vous?

On n’active pas la même chose chez l’enfant selon la tâche.
-> Tri taxonomique: pas d’effet d’âge: justification acceptables + majoritaire catégoriel
-> Paires taxonomiques: utilisation de justification correctes et incorrectes mais avec l’âge, il y a augmentation des justifications correctes - (avec une augmentation des justifications avec le terme catégoriel) et donc diminution des incorrectes.

Q10 : Quel est l’intérêt de demander des justifications?
Savoir si la réponse peut être considérée comme valable.

Q11 : Quel est le principal résultat mis en évidence dans cette recherche?

-> Pas d’évolution avec l’âge dans la production spontannée -> existence d’une coexistence inter et intra individuelle.
 -> Interindividuelles: selon les enfants, ils choisissent des catégories     schématiques ou taxonomiques en tri libre
 -> Intra-individuelles: parce que la majorité des sujets ne font pas librement un  choix taxonomique mais l’accepte si on leur propose.
 
Conclusion: Il existe une coexistence précoce mais avec l’âge, les enfants sont plus capables de passer d’un mode à l’autre. Avec l’âge, les enfants sont plus flexibles dans leur mode de catégorisation.
( avec l’âge, augmentation des justifications pertinentes).

Q12 : Comment pourrait-on l’expliquer.

Le tri libre et l’appariemment n’activent pas les mêmes conduites catégorielles.

Tri libre: schématique ou taxonomique à tout âge.
Appariemment: schématique à tout âge (quand on propose taxonomique, une minorité accepte).

Conclusion: Les catégories taxonomiques apparaissent plus en tri libre qu’en apparemment. Pourquoi?

a) parce que ça dépend probablement du nombre d’éléments dans la catégorie ( tri libre: 6 éléments ; apparemment: 2 éléments).

b) parce que deux consignes différentes peuvent amener deux interprétations différentes de la tâche.

c) la mise en concurrence explicite: le choix de l’enfant est encore sur la table (sous ses yeux) dans la tâche d’appariemment.
-> difficultés pour l’enfant d’ “inhiber” son choix
-> le passage de schématique à taxonomique est encore plus difficile.

TD n°3: Conservation et conversation

4 stade de développement:

- 1° sensori-moteur
- 2° pré-opératioire -> élaboration
 - - - - > 7 - 8 ans : quand l’enfant comprend que dans les transformations, il reste les invariants: il est conservant.
- 3° opératoire concret -> achèvement
- 4° opérations formelles

L’ancêtre de la conservation: la permanence de l’objet.

-> La permanence de l’objet: 2 acquis
 - erreur A non B : cache un hochet sous couverture A plusieurs fois et ensuite   on met le hochet sous un oreiller B : le bébé cherche toujours le hochet en A
        -> décalage vertical
 - pensée symbolique à 2 ans (fin du stade)

-> l’enfant pré-opératoire: sa logique se base sur la perception
        -> décalage vertical
-> L’enfant opératoire concret: sa logique se base sur la construction d’opérations

-> Décalage vertical: il se passe la même chose (même problème) à un niveau supérieur.

-> Opérations: actions réversibles intériorisées en pensée.   A   ->   B
                                                                                           <-
Tâche de conservation

-> des liquides:

-> du nombre : 6 ans
 - rangées :

 - transvasement (transvaser des jetons)

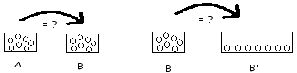
-> des substances : 6 ans

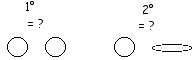
-> du poids : 7 - 8 ans
 

-> des longueurs : 6 ans

-> des volumes : 10 ans

Pour chaque épreuve: 3 sous-stades:

1° : non conservant:
-> stabilité des réponses données par l’enfant
-> si on fait une transformation, l’enfant dit que ce n’est plus pareil.
-> il se base sur un indice perceptif

2° intermédiaire
-> instabilité des réponses

-> il donne des réponses contradictoires car pour une grande transformation, il ne peut plus accepter l’égalité.

3° conservant
-> stabilité des réponses peu importe la transformation
-> justification: 3 types d’arguments:
 - identité: rien enlevé, rien ajouté
 - réversibilité par inversion (parfois appelé négation)
 - réversibilité par compensation (il se base sur deux dimensions: c’est plus haut,  mais c’est plus étroit).

Expérience 1: McGarrigle et Donaldson (1975)

Question 1:  Quelles sont les dimensions pragmatiques (pratique, efficace) en jeu dans les épreuves piagétiennes - et plus généralement dans toutes les épreuves d’évaluation - qui peuvent éventuellement conduire à mésestimer la compétence cognitive des sujets?

Pour Piaget, l’enfant devient conservant du nombre vers 6 ans.
-> Critique de Bryant: Il pense que ce n’est pas la notion de conservation qui est acquise tardivement par l’enfant, mais que les conditions de la situation expérimentale genevoise proposée empêche les sujets d’utiliser leurs connaissances (obstacle de mémorisation, conflit entre jugements, soit difficulté à effectuer un raisonnement inférentiel).
-> Proposition d’une tâche par McGarrigle et Donaldson (1975): l’enfant passe l’épreuce classique de conservation du nombre, mais au lieu que ce soit l’expérimentateur qui transforme une des rangées de jetons, un “teddy bear” maladroit tombe accidentellement sur le jeu et le dérange.

Question 2: Dans quelle mesure les épreuves modifiées de conservation mesurent-elles le type de compétence que Piaget étudiait avec ses épreuves classiques?

Dans l’expérience classique de Piaget:
- il existe une relation asymétrique enfant -expert. Alors l’enfant se demande pourquoi l’expert me reposerait la question s’il n’y avait rien de changé?
 -> L’ourson maladroit est une justification pratique à l’existence de la deuxième  question.
- la demande de justification peut faire croire à l’enfant qu’il s’est trompé, alors il change de réponse.
 -> Il n’y a pas de demande de justification, ni de contre-argument dans la tâche  de McGarrigle et Donaldson.

Dans la tâche de McGarrigle et Donaldson: le nombre de jetons est différent et la situation accidentelle ne comporte pas de demande de justification.
-> Et surtout, ces auteurs n’ont pas respecté l’intention de Piaget qui est d’étudier le problème que pose la transformation. En effet, pour Piaget, le problème de conservation consiste à reconstruire la transformation de manière à pouvoir l’annuler opératoirement.

Conclusion pour l’expérience de McGarrigle et Donaldson:
- Les enfants seraient donc en possession des mécanismes logiques nécessaires à la résolution de problème, mais ne sauraient les utiliser face à l’adulte, alors que face au “teddy bear”, ils en seraient capable.
-> Light et al. ont reproduit l’expérience du “teddy bear”. Ils ont trouvé des résultats moins nets, mais allant dans le même sens que ceux de McGarrigle et Donaldson.

Expérience 2: Light et al. (1979)

Question 1: Qu’est-ce qui, dans les expériences de Piaget pourrait sous-estimer la capacité des enfants?

Ils ont proposé une nouvelle tâche: il s’agit encore d’une épreuve de conservation du nombre à laquelle ils ont ajouté deux innovations:

-> ils motivent les sujets en les mettant dans une situation de jeu compétitif
 -> la demande de justification est justifiée par le fait qu’il faut bien s’assurer   pour le jeu que les deux enfants aient la même quantité de jetons.

-> au lieu de transvaser sans autre commentaire le contenu d’un verre B en un verre B’ (plus large que B), ils invoquèrent le fait que le verre B est ébréché et que l’enfant pourrait se blesser.
 -> justification pratique du changement de verre.

Résultats: les enfants sont plus précoces lorsqu’ils sont mobilisés (car ils sont libérés des deux questions)

Question 2: Dans quelle mesure les épreuves modifiées de conservation mesurent-elles le type de compétence que Piaget étudiait avec ses épreuves classiques?

- Les conditions expérimentales de la situation de Light et al. sont modifiées de façon important par rapport à celles de l’expérience classique.
 -> le jeu compétitif introduit risque de distraire l’enfant de la transformation.
 -> l’incident du verre cassé incite à négliger la transformation
En outre, le jeu compétitif tend à accentuer l’importance de l’égalité à établir entre les quantités initiales.
Enfin, de cette expérience sont aussi exclus les demandes de justification et les contre-arguments.

Conclusion:
- Autant Light et al. (1979) que McGarrigle et Donaldson (1975) semblent penser qu’ils obtiennent avec leurs réponses correctes, dans leurs situations expérimentales respectives, les mêmes résultats que ceux de l’expérience classique.
- Or, notre hypothèse (Bovet, Parrat-Dayan et Deshusses-Addor -1981) est que les problématiques en jeu sont différentes et donc que les résultats, quoique d’appartence identique ont un statut cognitif différent. Dans une seconde étape, nous nous occuperons de l’expérience de McGarrigle et Donaldson qui semble poser d’autre difficultés.

Expérience I : Bovet, Parrat-Dayan et Deshusses-Addor (1981)
-> Reprise de l’expérience de Light et al. en y ajoutant une demande de justification.

Procédure:

- Phase 1: A = B, deux verres identiques, mais B est ébréché. Les deux enfants remplissent les deux verres de bonbons. L’expérimentateur s’assure que les deux enfants considèrent les quantités comme égales.

- Phase 2: Consigne du jeu: l’expérimentateur explique qu’il s’agit d’un concours consistant à placer le plus vite possible les bonbons de son verre sur la grille.

- Phase 3: Transvasement de B et B’: l’expérimentateur feint d’exprimer la surprise devant le verre ébréché (B) et le remplace hâtivement par un verre nettement plus large (B’) dans lequel il transvase le contenu B.

- Phase 4: L’expérimentateur demande aux enfants si les quantités sont toujours égales ou non en A et B’ et donc si l’on peut ou non exécuter le jeu.

- Phase 5: Jeu: au cas où l’un au moins maintient l’égalité, il y a jeu.
- Phase 6: Les bonbons sont remis des grilles dans A et B’ respectivement. On repose la question des quantité à l’enfant en demandant à chaque enfant de justifier son jugement.

-> Ensuite, passation de l’épreuve classique et attente de réussite chez les enfants qui ont réussi l’épreuve de transvasement car l’épreuve du nombre rangée est atteinte plus précocement que celle du nombre transvasement, en général.

Résultats:

- Phase 4: 81 % de réussite (26 enfants /32)
- Phase 5: Jeu
- Phase 6: 25% de réussite (8 enfants /32)

-> Pourquoi cette différence entre la phase 4 et la phase 6 ? Problème d’attention?

Hypothèse: les nombreuses réponses correctes en phase 4 pourraient être liées à la situation spécifique de jeu et leur diminution en phase 6 serait due à la poursuite de l’interrogation par la demande de justification. -> contrôle A et contrôle B.

Contrôle A: absence du jeu compétitif (phase 5)

- Phase 4: 29% de réussite (5 enfants /17)
- Phase 6: très peu (2 enfant /17)

-> Conclusion des auteurs: le contexte de jeu masque la problématique de la transformation.

Contrôle B: si réussite à l'épreuve de nombre transvasement (phase 4 = 81%), alors réussite à l’épreuve des nombres - rangées (puisque plus précoce).

Résultats:

-> Contrôle B:
- Phase 4 (réussite au nombre-transvasement): réussite de 11 enfants /26  et échec de 15 enfants /26 ( = non conservants) au nombre-rangée.
- Phase 6 : réussite des deux épreuves de 8 enfants (sur les 11 en phase 4 qui ont aussi réussi les deux épreuves).

-> Expérience 1 (Bovet et al. reprenant Light et al.):
- Phase 6: réussite de 8 enfants /32
 
Conclusion: Les résultats de Light et al. et ceux de Bovet, Parrat-Dayan et Deshusses-Addor laisseraient supposer que l’enfant possède la structure de conservation à un âge beaucoup plus précoce que celui que l’on observe dans les résultats genevois à cette épreuve. (Car, en contrôle B, 11 réussissent les deux épreuves en phase 4).

Expérience II: Bovet, Parrat-Dayan et Deshusses-Addor
-> un problème demeure: est-ce le fait de demander des arguments à l’enfant qui entraîne ce faible nombre de réponses correctes ou est-ce le fait de demander ces arguments après le jeu, alors que l’enfant n’est plus motivé?

-> comment expliquer la faible réussite (25%) en phase 6?
Il faut intervertir la phase 5 avec la phase 6, cad, demander la justification avant le jeu.

Résultats:
-> Premier jugement d’égalité (phase 4): 9 enfants réussissent /11
-> Demande de justification: 2 enfants réussissent /11
-> jeu

=> Le problème, ce n’est pas la justification avant le jeu mais bien la DEMANDE de justification simplement.

Conclusion: il est abusif d’affirmer que tout enfant répondant correctement maîtrise la notion de conservation dans l’expérience de Light et al. et qu’il serait abusif de prétendre que les conditions expérimentales des épreuves classiques empêchent les enfants d’utiliser des structures opératoires qu’ils posséderaient.
-> Le jeu incite donc à une apparente maîtrise de conservation et la demande de justification nous montre que la notion n’est pas acquise chez l’enfant.

Expérience III: Bovet, Parrat-Dayan et Deshusses-Addor
-> Comment savoir si une réponse montre la conservation, sans demande de justification?

--> Le problème général étudié depuis le début du TD est de savoir si on peut se contenter d’une réponse oui - non à une épreuve de conservation.

-> Jusqu’à maintenant, on se fiait à la justification pour évaluer le niveau opératoire de raisonnement. Dans cette expérience, on juge le niveau opératoire de raisonnement par une action de l’enfant: action par composition quantitative.

1 : les enfants doivent mettre la même quantité de bonbons dans leur bocal (chaque bocal est différent par sa forme). L’expériementateur explique qu’il va y avoir un concours (placer les bonbons sur une grille) et insiste qu’il est important qu’ils aient des quantités égales pour le jeu.

2 : les enfants se mettent d’accord sur l’égalité; le jeu commence.
Résultats:
-> Deux types de solutions peuvent être données: soit unidimentionnelle (même niv. dans les deux verres) ou bidimentionnelle (tentative de compositions multiplicative: plus haut mais moins large).
-> La majorité des réponses sont unidimentionnelles: donc non conservantes alors que dans l’expérience de Light, il y avait 81% de bonnes réponses. Ces dernières n’étaient manifestement pas dues au raisonnement qui permet la conservation.

3. Situation contrôle: reprise des phases 1 à 5 de l’exp. I.

Résultats:

- 8 enfants jugent les quantités inégales après le transvasement de du verre ébréché B en B’. Donc, pour eux, le jeu n’a plus d’importance.
- 14 enfants répondent correctement après le transvasement.

Conclusion:
 
Ces deux dernières expériences, exp. III et contrôle, indiquent une fois de plus que les réponses correctes obtenues par la situation de jeu ne reposent pas, dans leur majorité, sur les structures opératoires concrètes.
 

Conclusion générale: Les réussites précoces aux épreuves modifiées de conservation n’évaluent pas la présence du groupement opératoire (tel qu’évalué par Piaget) dans la pensée de l’enfant. Seules une investigation par la justification ou par compositions quantitative permet d’attester de la présence de la structure (de groupement) opératoire.

Résumé:

Après avoir reproduit et confirmé l’expérience de Light, Buckingham et Robbins (1979), les auteurs élaborent une suite de situations expérimentales qui analysent la signification de la réussite à l’épreuve de conservation du nombre. Tous leurs résultats convergent à démontrer le statut non opératoire des réponses obtenues par Light et al.; dont la précocité paraissait problématique.

TD n°4 : Les schémas pragmatiques de raisonnement (SPR)

Les outils de la pensée

Piaget: schème (= outil) : structure d’action telle qu’elle se transfert ou se généralise lors de la répétition de cette action dans des circonstances semblables.

Schéma: succession d’événements ayant u but et apparaissant dans un contexte particulier (= routine sociale)

Routine sociale: outil d’organisation de la pensée (schéma pragmatique de raisonnement).

SPR: regroupement de règles (procédure pour arriver au but) et de buts (représentation de la situation à atteindre).

Limite du SPR: il est contextualisé donc on peut élaborer le schéma seulement dans un contexte particulier (il faut que l’habillage soit pareil ou très semblable à quelque chose de connu).

Selon Piaget: à l’âge adulte (logique formelle), on peut raisonner des proposition abstraites car on travaillerait sur les règles logiques directement.

-> la tâche de Wason infirme cette hypothèse:

Si j’ai un nombre pair, j’ai un consomme.

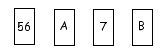
Quelles cartes retourner pour infirmer (ou confirmer) la règle?

56 et A

Seulement 10 % des adultes réussissent cette tâche (pour Piaget faudrait 81 %)

Si on prend une règle plus concrète, les gens se trompent beaucoup moins.

Deux explications:
-> Il faut avoir une expérience concrète de la règle pour réussir la tâche (ce qui expliquerait l’échec à la tâche de Wason).
-> c’est grâce au SPR (de raisonnement, d’obligation, ...)
Exemple: si je passe le BAC alors je suis en terminal

SPR de permission

-> Si A alors prédiction de B (retourner P)
-> Si non A alors prédiction de B? (ne pas retourner non p)
-> Si prédiction de B alors A (ne pas retourner q)
-> Si non prédiction de B alors non prédiction de A (retourner non q)

Si on arrive à trouver le raisonnement derrière la tâche, on peut activer le SPR approprié.
 

Expérience: peut-on transposer nos connaissances sur comportement de l’adulte à celui de l’enfant?

Population:
- 80 enfants âgés de 10 ans (opératoire concret)
- 80 enfants âgés de 14 ans (opératoire formel)

Facteurs: âge et habillage de la tâche.

Situation: énoncé de la règle et présentation des 4 cartes (p, q, non p et non q).

Conditions:
- Familière: si je suis assis en avant dans la voiture alors j’ai ma ceinture.
- Arbitraire: si voyelle alors nombre pair.
- Non familière: si je roule à plus de cent km/h, je dois avoir une voiture fluo
+ rationnelle : parce que quand une voiture roule vite, il faut qu’on la voit de loin (raison: sécurité).
- Non familière: si je roule à plus de cent km/h, je dois avoir une voiture fluo.

S20 < A2 * H4 >

VI1 : âge (10 ou 14 ans)
VI2: situation expérimentale (F, A, NF + R , NF).
VD: la performance (réussite, échec)

Trois théories = trois hypothèses

A - Piaget: à l’âge formel, on possède la logique en tout temps.
B - On peut utiliser les règles logique seulement si c’est une expérience concrète.
C - SPR (activé dès qu’on perçoit le rationnel de la règle)

HA : effet de l’âge et aucun effet de l’habillage (s’appuie sur le stade op. formel)
- 10 ans: échec à toutes les situations
- 14 ans Réussite à toutes les situations

HB : aucun effet de l’âge  et effet de l’habillage (s’appuie sur le familier)
- 10 ans et 14 ans réussite à F
- 10 ans et 14 ans échec à NF, NF+R et A

HC : aucun effet de l’âge  et effet de l’habillage (s’appuie sur le familier et/ou le raisonnement)
- 10 ans et 14 ans réussite à F et NF+R
- 10 ans et 14 ans échec à A et NF

Analyse des résultats:

Tableau 1:

-> effet d’habillage: f = NF + R > NF > A
-> pas d’effet d’âge

Tableau 2:

-> F : majorité de p et de non q
-> NF + R : majorité de p et de non q
-> NF: sélection de p, non q et q
-> A: sélection de p, non p et q.

Interprétation:

Peu importe l’âge (10 ou 14 ans), le même outil cognitif est utilisé

-> infirme Piaget
-> confirme SPR car réussite à F et Non F + R ce qui veut dire qu’on donne des réponses conforme à la logique mais sans se baser sur des règles logiques.

Conclusion

La familiarité n’est pas indispensable
La plausibilité (rationnel) est indispensable

Mais pourquoi NF > A si on utilise SPR?
Parce que la règle est plausible dans le Nf et donc la personne se construirait un SPR implicite qui permettrait la plausibilité. Car si c’est plausible, on peut activer le SPR de permission sinon, on ne peut pas.

TD n°5 : Le conflit socio-cognitif - Interactions et marquage social.

Le rôle des variables sociales dans le développement

Avant, les variables sociales étaient considérées externes au développement cognitif.

Pour Piaget, le conflit cognitif provoque un déséquilibre intra-individuel qui amène le changement.

En 1970, les variables sociales sont constitutives du développement = place centrale de l’environnement social.
-> l’intelligence s’élabore par les relations avec autrui = interindividuel.

==> Le conflit socio-cognitif (CSC) -> 1974

Le CSC est une confrontation de réponse différentes (divergence interindividuelle), socialement et cognitivement incompatible (déséquilibre intraindividuel).

Interactions symétriques

-> Deux individus de même niveau de fonctionnement, de même niveau de performance, de même rôle social, de même statut, mais de point de vue différent (centration différentes) afin de provoquer un CSC.

Trois phases:

1 - Prétest: individuel
2 - Entraînement: individuel et en dyade
3 - Post-test: individuel
 -> immédiat = idem prétest
 -> différé = même structure logique mais habillage différent - test le transfert   des connaissances.
Expérience 1

Population: enfants de 11 et 12 ans

Pré-tests: 2 tests d’intelligence logique

Tâche :
- trois critères:
Ordre de passage des fourmis : la couleur de la route, le profil de la route et la charge de la fourmi.

Conditions d’entraînement:
C1 : individuel + règle
C2 : individuel + découverte de la règle
C3 : côte à côte + découverte de la règle
C4 : coélaboration + découverte de la règle

Post test:
- immédiat : idem pré-test
- différé : ordre de personnes qui se saluent

Tableau 1 : Quartile

Q1 : 25% supérieur
Q3: 25% inférieur

Description des résultats:

- Les sujets ont de meilleurs performances au post-test différé après avoir eu un entraînement avec découverte de la règle.

- La coélaboration amène les bénéfices les plus importants.

- Pas de différence entre C2 et C3.

Expérience 2

Population: enfants de 11 et 12 ans

Pré-tests: épreuve d’intelligence

Tâche: allumettes
- Prendre un ou deux allumettes, celui qui prend la dernière à gagner.
-> Trouver la règle qui permet de gagner (multiple de trois) et de dire qui jouera le premier coup gagnant.
- Enfant contre ordinateur qui joue au hasard ou juste.

Conditions d’entraînement:
C1 : individuel + hasard
C2 : individuel + juste
C3 : dyade + hasard
C4 : dyade + juste

Post test:
- immédiat : idem pré-test
- différé : habillage et nombre d’allumettes prises sont différents.

Tableau 2: Quand l’ordinateur joue au hasard

1er exercice : habillage différent et 1 ou 2 allumettes.
2eme exercice : 1, 2 ou 3 allumettes

Description des résultats:

- La stratégie utilisées par l’enfant est différente quand l’ordinateur joue juste ou au hasard. -> la coélaboration à un effet quand l’ordinateur joue au hasard.

- Quand l’ordinateur joue juste, l’enfant tire profit et construit une stratégie par essai-erreur. L’enfant fait plus de partie en moins de temps. Il doit moins réfléchir.

- Quand l’ordinateur joue au hasard, il produit de l’incertitude et donne donc plus de travaille en commun et oblige à un raisonnement hypothético-déductif. Comme l’enfant est au début du stade formel (11, 12 ans), le raisonnement hypothético-déductif est difficile à mettre en place donc l’enfant à besoin de l’autre.

Expérience 3

Population: enfants de 11 et 12 ans

Pré-tests: épreuve d’intelligence

Tâche: deviner, avec le moins “d’opérations” possible, quel cube (parmi 8) est plus léger que les autres.

Tableau 3 : schéma cognitif économique

Schème pragmatique: 3 pesées ( 4/4 ; 3/3 ; 2/2)
Schème économique: 2 pesées ( 3/3 ; 1/1)

Le travail en dyade permet d’éviter, le plus souvent, l’application du schème pragmatique.
____________________________________________________________

* Quels pourraient être les processus responsables des effets bénéfiques des dynamiques interactives?

En général, l’entrainement en dyade amène plus de progrès qu’en individuel.

* Est-ce qu’il y a toujours progrès lorsque l’enfant est entraîné en dyade?
Non

* Y a-t-il toujours progrès chez les deux enfants entraînés dans la même dyade?
Non, ça dépend de la résolution du conflit et de la manière de rechercher la solution. Quand il y a CSC, il y a progrès.

Deux types de résolution (dépassement) de conflit
-> socio-relationnel: pas de progrès (un se soumet à l’autre = absence de réorganisation cognitive)
-> socio-cognitif: progrès car ils confrontent leurs réponses et doivent coopérer activement pour construire une solution au problème = réorganisation cognitive

* Pourquoi la résolution d’un problème de manière socio-cognitive est-elle source de progrès?
Parce qu’elle met en oeuvre un CSC. Le fait de devoir donner seulement une réponse oblige au dépassement du déséquilibre inter-individuel créé. Il y a donc progrès par intériorisation des coordinations interindividuelles.

-> Destabilisation et contrôle réciproque sont des fonctions des interventions réciproques. Elles sont bénéfiques dans les interactions parce que:
 - elle destabilisent: elle conduit à des remises en cause de l’enfant, à des changements de représentation de la tâche et à des changements de procédure de résolution.
 - elle demande du contrôle qui favoriserait une gestion consciente du déroulement de l’activité de résolution.
 

Conclusion sur CSC
 
Le bénéfice du CSC dépend des compétences initiales de l’enfant (pré-requis scolaire et cognitif).

Ce n’est pas nécessaire qu’un des deux enfants ait plus de compétences que l’autre pour qu’il y ait progrès.
Le marquage social (MS)

Marquage social: norme sociale (signification sociale pour l’enfant) = règles qui soutendent la compréhension de la tâche doivent exister dans la réalité. La norme sociale est associée à une norme intellectuelle.
 

Expérience 4

Population: enfants de 5 ans 9 mois et de 6 ans 5 mois non conservant à la longueur.

Pré-test: conservation de la longueur

Deux situations expérimentales:
- MS : attribution (enfant - adulte) sociale de bracelets
- sans Ms : attibution de bracelet à deux cylindre

Règle: enfant met des objets plus petits que l’adulte.

Tâche:
2 bracelets:
T1 :    Même longueur? + attribution
T2   + attribution
T3 :    + attribution

On fait une contre-suggestion à l’enfant lorsqu’il répond à la question du T1. (si ils ont la même longueur alors pourquoi il va bien à l’adulte et aussi à l’enfant?)

Expérience 5

Population: Enfants de 4 ans 1/2 à 6 ans et 1 mois

Pré-test: conservation des liquides: on garde les non-conservants.

Règle: droit acquis au partage égal

Conditions:
- Individuelle + MS
- Individuelle sans MS
- Collective + MS
- Collective sans MS

Tâche: expérimentateur verse:

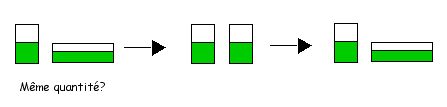
Provoquer le conflit: il recommence la procédure.

Post-test:
-> immédiat = pré-test
-> différé = conservation du liquide, du nombre et de la substance pour savoir si la conservation s’est généralisée.

Résultats (tableau 8)

Le Ms aide à la conservation

Résultats (tableau 11)

Le Ms aide à la conservation aussi bien en collectif qu’en individuel.

Résultats (tableau 12)

Ceux qui ont progressés ont un bon score de généralisation
Ceux qui n’ont progressés pas ont un moins bon score de généralisation.

Interprétation pour les deux expériences du MS

Quand on place des enfants dans une tâche avec MS, ils ont deux façons de résoudre la tâche:

- un schème cognitif = réponse cognitive
- un schème social = réponse sociale

Ces deux façons créent u conflit intraindividuel par rapport aux deux réponses possibles: donc processus mis en oeuvre: CSC

Quand il y a dépassement du conflit intra-individuel, il y a progrès.

Pourquoi on ne retrouve pas de différence entre les performances lorsque l’individu est entraîné individuellement ou collectivement?
Parce que le conflit est généré par nos schèmes et non par l’autre. (donc en collectif, cela ne change rien).

==> Le CSC amène le progrès.

Mais ATTENTION, le progrès n’est pas du à l’habillage familier mais bien au conflit (CSC) provoqué par la confrontation du schème cognitif et social.

TD n°6 : Contribuer à l’enseignement des mathématiques : Rightstart

Deux problèmes chez Piaget
- La nature des structures logiques
- L’hermétisme de ces structures logiques à toutes entreprises éducatives.

SCC : Structures conceptuelles centrales

Répertoire structuré de connaissances (préalablement constituées). Ces structures donnent du sens aux situations qu’on rencontre en donnant un contexte cognitif.
-> La SCC est un filtre à travers lequel on perçoit les informations.

-> Houdé: donc, tout le monde ne se représente pas le problème de la même manière puisqu’on n’a pas tous les mêmes connaissances.

Deux dimensions importantes des SCC
- elles sont centrales mais intra-domaine (chez Piaget, interdomaine), c’est-à-dire une structure centrale pour chaque domaine de connaissance (donc indépendante des contextes).

Note: intra-domaine évite le problème du décalage horizontal.

- L’acquisition des SCC est liée en partie à une transmission culturelle et scolaire
-> On peut donc intervenir pour favoriser l’acquisition des structures, ce qui n’est pas le cas dans la théorie de Piaget.
-> c’est pour cela que Robbie Case à mise en place un programme d’enseignement!

La structure conceptuelle centrale numérique

Elle se développe en trois stades :

Pré-dimensionnel (4 ans) -> uni-dimensionnel (6 ans) -> Bis-dimensionnel (8 ans)
(-> 4° vectoriel - 12 ans)

1° Pré-dimensionnel
- dénombrement
- Schème de jugement quantitatif global

-> Ces deux schèmes de sont pas coordonnés : l’enfant ne peut pas utiliser le dénombrement pour porter un jugement quantitatif global.

Donc, l’épreuve de la balance n’a pas de signification arithmétique pour l’enfant de 4 ans.

2° Uni-dimensionnel: l’enfant a construit la SCC numérique :

Il coordonne les deux schèmes: il peut donc réussir les items avec des différences perspectives faibles

-> Schème développé : schème de quantification par dénombrement.

3° Bis-dimensionnel : le schème de quantification par dénombrement devient automatique et libère de la mémoire de travail.

-> L’enfant peut prendre en compte une autre dimension (mais les deux dimensions ne doivent pas varier en même temps)

4° Stade vectoriel : permet de coordonner les deux dimensions pour résoudre les problèmes impliquant une solution multiplicative et vectorielle.

Description du graphique :

Ligne A : Connaissance de la graphie des chiffres (reconnaissance de l’écriture).

Ligne B : Connaissance des étiquettes verbales des chiffres.

Ligne C : Connaissance du nombre de pas entre les nombres.
     Mental action online = routine cognitive du pointage

Ligne D : Cardinal (valeur associée à la représentation perceptive de chaque nombre).

Crochets: Notion de peu et beaucoup

Tous ces concepts sont intereliés.

Note: On a dit que la représentation d’un problème dépend des connaissances de chacun. Quand on n’a pas acquis la SCC numérique (donc avant 6 ans), le problème de la balance ne peut pas avoir de signification arithmétique.

L’ACQUISITION DE LA SCC NUMÉRIQUE EST LA CIBLE DU PROGRAMME RIGHTSTART.

Le Programme Rightstart

Il est destiné à des enfants de milieu socio-économique défavorisé, avant l’entrée en primaire (car on a constaté une inégalité : les enfants ne niveau socio-économique défavorisé ont tendance à ne pas avoir développer entièrement la SCC numérique avant l’entrée en primaire).

Objectif principal: fournir aux enfants défavorisés des expériences qui permettent de maîtriser et développer convenablement les différentes dimensions (A, B, C, D, E) de la SCC numérique afin d’entrer au primaire en étant armés des outils cognitifs nécessaires afin de tirer profit de l’enseignement qu’ils reçoivent (mathématique dans ce cas). Rightstart = bon départ.

Objectif spécifique: chaque objectif spécifique correspond à une dimension de la SCC numérique.

Exemples:

Leçon 2 de l’unité 3

- Les dimensions de la SCC à acquérir
-> ligne C: il compte à haute voix un par un tous les jetons qu’il met en banque (routine cognitive du pointage).
-> ligne D: la couleur des jetons permet à l’enfant de voir l’ensemble global (cardinal).
-> ligne E: super garçon / fille enlève un jeton -> comparaison avant-après (quantité).

+ activité de renforcement

=> Cette leçon met principalement en relation la ligne C avec la ligne D :
 -> principe éducatif de Case : transposition conceptuelle (on se base sur    quelque chose de déjà connu (compter) pour arriver à un nouveau concept (la    quantité).
 -> principe éducatif de Case : diversité représentationnelle ( 1° banque, 2°    enfants = central mais non contextualisé).

Leçon 3 de l’unité 9

- Les dimensions de la SCC à acquérir
-> ligne C: associer un bonbon à chacune des étiquettes verbales (routine cognitive du pointage)
-> ligne D: qui commence? celui qui a le plus grand nombre? (cardinal)
-> ligne E: par rapport aux cartes: fée = +1, monstre = -1

On arrive à une véritable addition (variation: manger le même nombre de bonbons).

Notes en plus:

-> la demande de justification permet d’observer le raisonnement derrière la réponse. D’une certaine manière, les arguments expriment les opérations impliquées par la notion de conservation.

-> Rappelons que le schémas traditionnel des expériences classiques de conservation est le suivant: on présente à l’enfant deux objets - A et B - équivalents soit au point de vue du poids, soit de la longueur, soit du nombre, etc. L’enfant reconnaît cette égalité. L’objet B est ensuite transformé en B’ (changement de forme, déplacement, transvasement en des récipients de différentes dimensions, etc.). L’enfant doit alors déterminer la relation existant entre A et B’ ( =, différent, plus léger, moins long, plus nombreux, etc.)

-> L’enfant arrive d’abord à réussir l’épreuve des nombre-rangee et ensuite des nombre-transvasement: 1° Nombre-rangée; 2° Nombre-transvasement.