|
www.angelfire.com/dragon/letstry
cwave04 at yahoo dot com |

|
|
|
Continuous time finite automata
So far our discussion has been revolving around finite automata from
the
viewpoint of software. But finite automata are no less (arguably even
more) important in the field of hardware, and softwares that
directly
interact with hardware. A robot, for example, is armed with
finite automata from top to toe.
In this section we shall take a look at how finite automata are used in
hardware. These automata are special cases of the automata we have
discussed, and we shall call these continuous time finite
automata.
So far our finite automata were all working in "discrete time". This means that the inputs came one by one, and after each input the DFA produced the output, updated the state,
and then waited for the next input. If we assume that the inputs arrive every second then it is like a short burst of activity at every tick of the second-hand followed by no activity until the next tick.
In the world of hardware, however, time is continuous. Inputs and outputs are voltages through wires and every wire has some voltage or other all the time.
Is it possible to design a DFA that takes continuous inputs and produces continuous outputs?
The DFAs we have discussed so far do not appear to be applicable here, right? Well, appearances are deceptive, as we shall soon see. But first a little example to clarify the difference between discrete time and continuous time.
A little silly game
Here is a small roleplaying adventure game for you.
The storyline is like this: You are a gunman figting against a tank.
Your gun is strong enough for the encounter, but
the tank is behind a moving shield-like armour that makes it
immune to
gunfire. However, you also have a disarmer which deactivates the
armour. After
you have disarmed the tanker
you can try to kill it with your gun. You will need two firings
for that, as the first bullet will only injure the tank, but not
kill it. If you do not succeed in killing the tnk within three
steps (i.e., three button clicks) then the tank will kill
you.
In a textbased version the game looks like this:
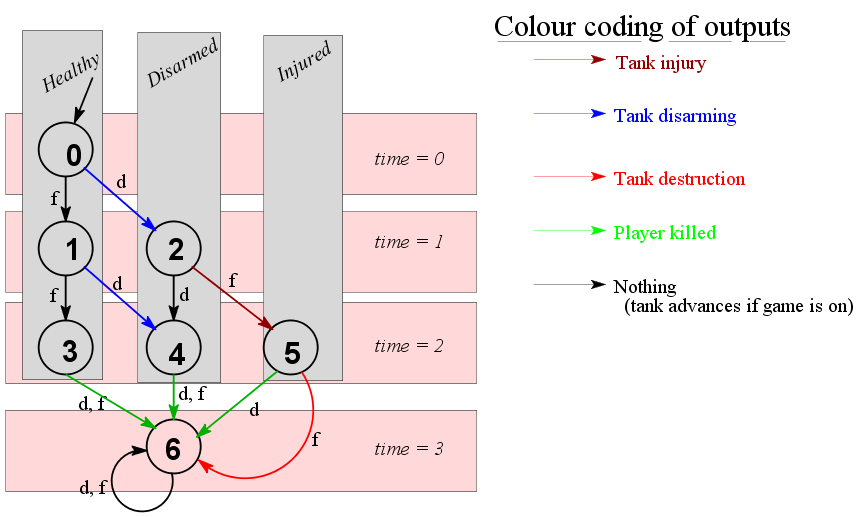
Here is the transition diagram. We have 7 states (numbered 0 to
6). initial state. State 6 is the final state (where either the
player or the tank is destroyed). All the other states record two
info: the elapsed time and the condition of the tank (healthy,
disarmed or injured).
The rectangles in the background help you see this clearly. The
arrows are labelled with only the inputs (d for disarm, f for
fire). The outputs are shown using the colour of the
arrows.
Does this game really
create the same feeling as you would feel if you faced
a tank charging straight at you? No! Here it is obvious that
you are merely playing a game against the tank where the MOVES
ALTERNATE. Howsoever powerful the tank might be, it has to
wait patiently until you make your move. That is to say time is
discrete here. It is marked by ticks that correspond to
your pressing a button. Nothing can happen between
two ticks.
A real enemy, however, will not wait for you to take action. It
will move at its own pace unless you manage to thwart its attack
in time. In other words, in real world time is continuous.
To see why our code failed to have this realistic behavior
consider how you would implement the automton in C. At each state
we emit some particular message on the screen, and then we
wait for your response. It is this waiting
that blocks everything else until you click on a button.
We refer to this type of behavior as blocking.
Here is a graphics version of the same game. You must first click
the "START" button to start the game.
This game is much closer to reality. The tank seems to have
a life of its own. Even if we do not actively do anything the
tank now continues to approach, i.e., the output is
produced in continuous time. However, at the same time it is
also continuously listening for any input from the user, since
the instant we click "DISARM" the armour vanishes.
How is the code managing both these tasks
simultaneously? What we are doing here is called
multitasking, and involves a little cheating.
Actually, behind the scene we are still using discrete time, but
the ticks are so closely spaced (say once every millisecond) that
it looks like continuous time. At these ticks we are not waiting
for any event to happen. We are merely scanning the present
conditions of the inputs. For example, the computer may scan
a button one million times between a button press and its
subsequent release. Viewed in this micro-time-frame a button is a
source of input that can be in either "pressed" or "released"
condition.
Note that we have to keep track of three sources of inputs: the
two buttons
and the timer (that controls the tank). The input a each tick
consists of the current status of these. Each of the buttons can
be either pressed or released. The timer can be either running or
timed out (when the tank has killed you).
So at the level of milliseconds there are actually 6 inputs:
- Timer on, "Disarm" released, "Fire" released:
(abbrev: tdf),
- Timer on, "Disarm" released, "Fire" pressed:
(abbrev: tdF),
- Timer on, "Disarm" pressed, "Fire" released:
(abbrev: tDf),
- Timer out, "Disarm" released, "Fire" released:
(abbrev: Tdf),
- Timer out, "Disarm" released, "Fire" pressed:
(abbrev: TdF),
- Timer out, "Disarm" pressed, "Fire" released:
(abbrev: TDf),
Since you have only one mouse pointer, you cannot press both the
buttons simultaneously! So there is no DF case. Also, because of
the same reason the input dF and the input Df cannot occur side
by side.
You'll need some space of time to take the mouse pointer
from one button to the other, thus inserting the input tdf or Tdf
in-between.
We still have basically the same set of outputs, but with
one important difference. In the discrete case the inputs were
events that we waited for. In the continuous case the inputs are
conditions of input sources that we merely observe. In the
discrete case the outputs
were events that we caused to happen (like "injure the
tank"). In the continuous case the outputs will be the possible
conditions
that can prevail (like "the tank is injured").
- Tank disarmed
- Tank injured
- Tank destroyed
- Player killed
- Tank healthy
So we need a finite automaton to produce these 5 outputs from the
6 inputs above. Clearly, the discrete time automaton mentioned
earlier cannot do the job, since its input set was of size 2,
while our input set is of size 6.
We shall learn later how to design a finite automaton in this
situation.
For now here is a finite automaton that
answers our need.
We have used some abbreviations here: T** stands for all inputs
starting with a T (i.e., Tdf, TdF, TDf). Similarly, ***
denotes the set of all possible inputs.
Here 0 is the initial state. By the way, it can be shown that we
can never achieve our goal here with a DFA with fewer
states.
The following interactive animation may help you to understand
the workings of the automaton. First click START. Then click the
the other two buttons. But in order to see the details, hold a
button for some time before releasing it. (This does not apply to
the START button, which may be clicked in the ordinary way.)
You'll see that
pressing a button triggers some action while releasing it may
trigger a different action.
This DFA is an example of what we call a continuous time
DFA.
If you play with the above animation for some time you will
notice that when you are not changing the input (e.g., while
holding a button down) the little
red blob keeps on circling around a loop at the current state.
This is the characterising feature of a continuous time
DFA. Before we discuss why this is important let us precisely
write down the definition of a continuous time DFA.
Defn: Suppose that you have a DFA with output function
f and next state function g. This DFA will be called a
continuous time DFA if it satisfies two conditions:
- If for any two states s,t and any input
in we have t = g(s,in), then we must also have
g(t,in) = t.
- If for any two states s,t and any input
in we have t = g(s,in), then we must also have f(t,in)
= f(s,in).
The conditions can be more readily digested using the diagram
below.
Here s and t are any two states.
Whenever we have the red arrow we must also have the green self
loop. Here in is any input and out is any output.
This means that
as long as the input condition that caused the state transition
(from s to t) prevails, the current state must not
change, and the same output condition must prevail.
What's so magical about this condition?
Our main aim is to create the illusion of continuous time. For
this we are actually using a discrete time scale with a high
enough resolution, e.g., milliseconds. Now suppose
that you
press the FIRE button before time out. Until you release the
button each
millisecond tick produces the input tdF. Being only an ordinary
mortal, you can never predict the duration of the button press
correct to the nearest millisecond. So the exact number of tdF's
that the finite automaton sees is also not predictable. All that
can be guaranteed is that there will be a stretch of tdF's. The
length of the stretch will vary randomly from one press to
another, and is not important. The condition above makes the DFA
sensitive to the stretch, but insensitive to the length of the
stretch, by providing the green loop to ``eat up'' the stretch.
Notice, by the way, that the automaton for the text version violates
this condition.
|