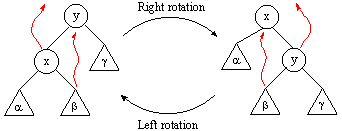
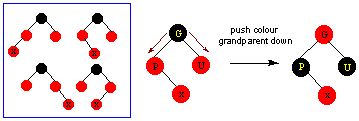
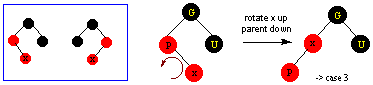
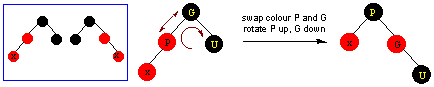
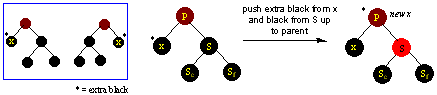
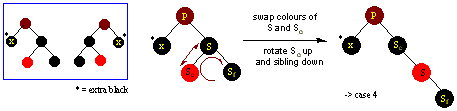
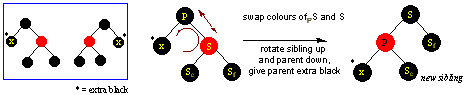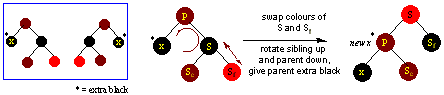Piglet's Home Page/Computer Science Home
| T(1) | = | 1 | T(n/2) | = | 2T(n/2/2) + n/2 | |
| T(n) | = | 2T(n/2) + n | = | 2T(n/4) + n/2 | ||
| = | 2(2T(n/4) + n/2) + n | T(n/4) | = | 2T(n/4/2) + n/4 | ||
| = | 4T(n/4) + n + n | = | 2T(n/8) + n/4 | |||
| = | 8T(n/8) + n + n + n | |||||
| = | 2kT(n/2k) + kn | |||||
| = | nT(1) + log2n * n | (using 2k = n) | ||||
| = | n + nlog2n | |||||
| (BASIS) | let n = 1; then T(n) = 1 (by definition of T), and n + nlogn = 1 + 1*0 = 1 | ||||
| so works for n = 1 | |||||
| (STEP) | assume works for some value k ie. T(2k) = 2k + 2klog22k (Induction Hypothesis) | ||||
| does k+1 work? ie. is T(2k+1) = 2k+1 + 2k+1log22k+1? | |||||
| Well, | T(2k+1) | = | 2T(2k) + 2k+1 | (by definition of T) | |
| = | 2(2k + 2klog22k) + 2k+1 | (by Ind. Hyp.) | |||
| = | 2k+1 + 2k+1k + 2k+1 | (as log22k = k) | |||
| = | 2k+1 + 2k+1(k + 1) | ||||
| = | 2k+1 + 2k+1log2(k + 1) | ||||