1 <---Numerator
-
3 <---Denominator

• The top number (1) is called the numerator
• The bottom number (3) is called the denominator
• This fraction means 1÷3 (That is, 1 divided by 3)
• It also means, one thing cut-up or broken into three pieces
• We would read this fraction as one-third

EXAMPLE:
one third of the circle is not shaded

Sometimes it's hard to remember numerators from denominators. Try letting the "D" in denominator remind you of the "D" in down. And, the "U" in numerator can remind you of the "U" in up.

ADDING FRACTION

Adding Fractions with Same Denominator

Steps to add fractions with the same denominator

1. Add the numerators and place that sum over the common denominator
2. Simplify

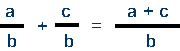
EXAMPLE:

Question: 1/4 + 1/4
Solution:
Step 1: 1/4 + 1/4 = 2/4
Step 2: 2/4 = 1/2

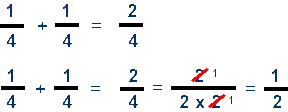
Adding Fractions with Different Denominators

Steps to add fractions with the different denominators:

1. Find the Least Common Denominator (LCD) of the fractions
2. Build each fraction so that both denominators are equal.
3. Add the numerators of the fractions
4. Simplify the Fraction

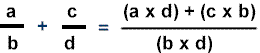
Just a reminder of how to find LCD OF THE DENOMINATORS

The steps to find LCD

1. Factor each of the denominators into primes
2. Count the number of times each prime number appears in each of the factorization
3. Write down prime number as many times as you counted for it in step #2.
4. The least common denominator is the product of all the prime numbers written down.

Question: Find the LCD for 1/5, 1/6 and 1/15.
Solution:
Step1: Get the Prime for each denominator
Prime factorization of 5 is 5
Prime factorization of 6 is 2 x 3
Prime factorization of 15 is 3 x 5

Step2: Count the number of times each prime number appears in each of the factorizations
The count of primes in 5 is one 5
The count of primes in 6 is one 2 and one 3
The count of primes in 15 is one 3 and one 5

Step3: For each prime number, take the largest of these counts. So we have
The largest count of 2s is one
The largest count of 3s is one
The largest count of 5s is one

Step4: The least common denominator is the product of all the prime numbers written down
2 x 3 x 5 = 30
Therefore, the least common denominator of 1/5, 1/6 and 1/15 is 30.

SUBTRACTING FRACTION

Subtracting Fractions with Same Denominator
To Subtract Fractions with Same Denominator follow the steps in Adding Fractions with Same Denominator but now with a differnet sign.

Subtracting Fractions with Different Denominator
To Subtracting Fractions with Different Denominator follow the steps given in Adding Fractions with Different Denominator but with differnt signs.

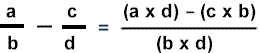
TRY OUT the practice problems
In the game the addition sign "+" is denoted as * because of technical problems. Sorry for the inconvenience.

PLAY