If a and b are real numbers, then a + bi is called a COMPLEX NUMBER. The number a is called the REAL PART of the complex number and the number bi is called the IMAGINARY PART. If a + bi = x + yi, then a = x and y = b. If x + yi = 7-5i then x = 7 and y = -5. Usually we say z = a + bi where z is a complex number.
Before we learn to deal in operations with complex numbers, it is important to know how the operator i is used.
The sqr.root -1 = i
And i2 = ( -i)2 = -1.
Also, i3 = (i2)(i)=-i.
So i4=( i2)( i2)=(i2)=1.
Thus, i5 = (i4)( i) = i.
So i6=( i4)( i2)=(i2)=-1.
Also, i7 = (i4)(i3) = -i
And i8 =( i4)( i4)=(i4)=1.
Hence we see that successive integral powers of i run thru the cycle: i, -1, -i, 1 as given in the above table.
If A = a + bi and B = c + di then A + B = B + A = C
C = (a + bi) + (c + di)
C = (a + c) + (b + d)i
C = a + c + bi + di
If A=7+5i and B =7+5i then C=7+7 + 5i + 5i and C = 14 + 0i
If A=7-5i and B =7+5i then C=7+7 - 5i + 5i and C = 14 + 0i
If A = a + bi and B = c + di then A - B = B - A = C
C = (a + bi) - (c + di)
C = (a - c) + (b - d)i
C = a - c + bi - di
If A=7+5i and B=7+5i then C=7-7 + 5i-5i and C= 0 + 0i
If A=7-5i and B=7+5i then C=7-7 + 5i-5i and C= 0 - 0i
If A = a + bi and B = c + di then A * B = B * A = C
C = (a + bi) * (c + di) , C = (ac + bdi2)+(ad + bc)i
(remember: i2=-1) C = ac - bd + adi + bci
If A=7+5i and B=7+5i then C=49-25+35i+35i and C= 24 + 70i
If A=7-5i and B=7+5i then C=49+25 + 35i-35i and C= 74 + 0i
The conjugate of a complex number z = (x,yi) = x + yi
is the complex number z*=(x,-yi) = x - yi.
Sum of conjugates: (a+bi) + (a-bi) = 2a (real number)
Difference of conjugates: (a+bi)-(a-bi)=2bi (complex number)
Product of conjugates: (a+bi)(a-bi) = a2+b2 (real number)
Division of a complex number by another complex number is accomplished by multiplying both numerator and denominator by the conjugate of the denominator.
(a+bi)/(c+di)=(a+bi)(c-di)/(c+di)(c-di)
=(ac+bd)+(bc-ad)i/c2+d2
(3+i)/(2-i) = (3+i)(2+i)/(2-i)(2+i)
= 6+5i+i2/4-i2 = 5+5i/5 = 1+1i
A function is the relationship between two or more variables and constants. f(z) represents a function of z. The notation means "function of z" and does not mean multiplication. The first function we will explore is the function for Julia sets which is: f(z) = z2 + c. For example we can say f(z) = z2 + (0,0i) where c = (0,0i). To find other Julia functions all we have to do is change the value of c. By now you realize that (0,0i) is a coordinate in the Z or complex plane. That is, it represents where we will look for a Julia fractal in the Z plane. The famous Mandelbrot fractal uses the function f(z) = z2 + c where the value of c is not a fixed coordinate; it is different for every point examined. There are unlimited functions f(z) that can be used to form fractals.
When we process a complex number by some f(z) we look at the result and see if it is going to escape to infinity or to be captured by an attractor. If there is no real indication we send the result back into the function f(z) and process it again and again until we have a good idea of how the result will behave. The sending of the result back into the function many times we call ITERATIONS. Usually 100 iterations is all that is necessary to form a fractal. However, if we are looking very deep into a fractal (that is we are looking at it 10,000x or 1,000,000x it's normal size) then we have to increase the number of iterations or loose fine detail in the fractal.
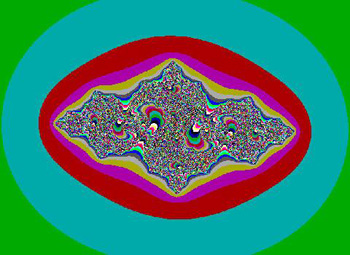
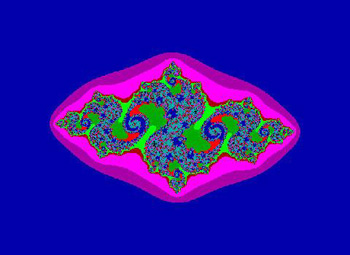
Looking at "black and white" fractals is not very interesting. The beauty in fractals is not only their shape but in their colors. For a simple fractal that needs only 100 iterations only 16 different colors provide an interesting picture. Black is used to show that the point is captured and part of the fractal. Other colors indicate the number of iterations required to escape to infinity. Color #1 is assigned for one iteration, color #2 for two iterations etc. After the 16 colors have been assigned to the first 16 iterations, the cycle of colors is repeated for the next set of 16 iterations. This way each color is used a little over 6 times for the fractal picture. For fractals that require hundreds of iterations, each color may be used for each set of 10 iterations. It is possible to use the 256 color scheme but this is not usually done because to many colors spoil the overall fractal picture. Of course any color scheme that one likes can be used.
Here is an example of a 16 color JULIA fractal showing the effect of enlargement and how different iterations cause a change in the fractal picture.









Here is an example of a JULIA fractal showing the effect of how too many colors can hide the beauty of the fractal.