|
|
 Simplifying radicals Simplifying radicals
 Objective: To simplify square roots in which the radicands contain variables raised to even or odd powers. Objective: To simplify square roots in which the radicands contain variables raised to even or odd powers.
There are two properties that go along with square roots of the form 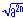 , where the value of a is positive, and 2n is an even number. , where the value of a is positive, and 2n is an even number.
 Square Root Property of Even Powers: For every even number 2n, the square root of Square Root Property of Even Powers: For every even number 2n, the square root of
a2n = the square root of an + n = the square root of (an)(an) = an, where a > 0
 Square Root Property of Odd Powers: For every odd number 2n + 1, the square root of Square Root Property of Odd Powers: For every odd number 2n + 1, the square root of
a2n + 1 = the square root of (a2n)(a1) = the square root of (an)(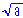 ), where a > 0. ), where a > 0.
Examples:
a.) Simplify the square root of (25a8b18)
= 4 * 5 * a4 * b9
= 20a4b9
b.) Simplify 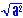
= a |
 Simplifying radicals
Simplifying radicals Objective: To simplify square roots in which the radicands contain variables raised to even or odd powers.
Objective: To simplify square roots in which the radicands contain variables raised to even or odd powers.