|
|
 Problem Solving: quadratic equations
Objective: To solve geometric problems that lead to quadratic equations
There are 4 methods for solving quadratic equations:
(1) Square root property
(2) Factoring
(3) Completing the square
(4) Quadratic formula
Methods (3) and (4) can be used for any quadratic equation, but methods (1) and (2) are used when an equation has no middle term.
Example: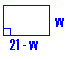
a.) The rectangular floor of a tree house is constructed so that its perimeter is 42 ft. and its area is 104 ft2. Find the width and the length of the floor.
Draw a diagram and represent the data. If you need to solve a quadratic equation, try factoring first. If that is not successful, use the quadratic formula.
Let w = the width and l = the length.
The perimeter formula is p = 2l + 2w
42 = 2l + 2w
21 = l + w
l = 21 - w
A = lw
104 = (21 - w)w
104 = 21w - w2
w2 - 21w + 104 = 0
(w - 13)(w - 8) = 0
w = 13 or w = 8
1.) If w = 13 then l = 21 - 13 = 8
2.) If w = 8 then l = 21 - 8 = 13
Try both combinations in the original equation. Only the second combination works. Thus, the width of the floor is 8 ft and the length is 13 ft. |
