Site hosted by Angelfire.com: Build your free website today!

  

home  |  email us  |  glossary 

Multiplying & dividing radicals
 Objectives: To multiply or divide, and simplify expressions containing radicals, and to simplify expressions by rationalizing the denominator

To multiply two expressions that contain square roots, use the property that states that the
square root of a multiplied by the square root of b = the square root of (ab)

Similarly, To divide two expressions that contain square roots, use the property that states that the
square root of a divided by the square root of b = the square root of (a / b) This property extends to all positive numbers and is called the Quotient property for Square Roots.
Note: A radcal in simplest form contains no radical in the denominator. The numerator will not always be exactly divisible by the denominator. In such cases, it is necessary to rationalize the denominator. This is done multiplying both the numerator and the denominator by the least square root possible to make the radicand in the denominator a perfect square.

Examples:
a.) Simplify *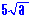
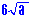
answer: 30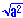

b.) Simplify 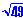divided by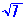
answer: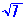

c.) Rationalize and simplify /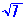
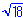
Multiply the top and bottom by
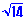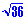= / answer: 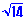/ 6