Taylor Polynomials

Curiously, one of the main uses of calculus in this day and age of calculators and computers is in approximating functions and function values. We consider here one very useful approximation, the Taylor polynomial, and see how it is used in calculations and in developping theory.

Taylor's Theorem tells us that provided we are reasonably careful (what this means will be explained more fully when we reach Taylor polynomials), we can approximate any function by a Taylor polynomial. If we increase the degree of the Taylor polynomial, the approximation at any fixed x improves, and the interval over which we get a reasonable approximation lengthens.

Taylor Polynomials In Calculations

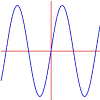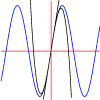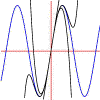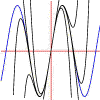
Taylor polynomials often give good approximations of function values fairly easily. For example, the image(s) you see above are the graph of sin(x) and the graphs of the degree 1, 3, 5, 7 and 9 Taylor polynomials for sin(x). Notice how well even the degree 1 polynomial agrees (to 2 decimal places) with the sine graph close to 0, and notice that each higher degree polynomial approximates the sine curve well for larger and larger values of x. In fact, if you do the calculations you also find that the approximations improve for any given x as the degree rises:

The ninth degree Taylor polynomial for sin(x) already approximates sin(Pi/4) to within 2 billionths. Not bad!

If you are taking Math 1220 you will see more applications of Taylor polynomials: most anti-derivatives can not be found exactly, but Taylor polynomials allow for reasonable approximations.

Taylor Polynomials In Theory

Let's look at some problems first:

1. If we drop a ball far above the earth's surface we know that the acceleration due to gravity will be given by K/r² where r is the distance between the center of the ball and that of the earth, and K is a constant. However, when dealing with objects close to the earth's surface we assume the acceleration is constant. How can we justify using two different formula for the same phenomena?
2. Bacterial growth in a medium is often modeled using exponentials, however, exponential growth can obviously not be a good model for "old" colonies: if growth were exponential, there would be more bacteria than medium! How can we model the growth of "old" colonies?

Both these problems are dealt with using Taylor polynomials: in the first we show that the "error" in assuming acceleration is constant is small, in the second we approximate the bacterial growth by a polynomial. Notice that in the first problem we have a function to play around with, while no such function exists in the second. We have a nice equation for acceleration, and only want to show that it is "almost" constant near the surface of the earth. In the second problem we are trying to guess at a reasonable function for the population. It is Taylor's Theorem that tells us what the guesses should be, and why.

Falling Ball

For the falling ball, let R be the radius of the earth and h be the height of the ball above the earth. Using Taylor polynomials we can show that K/(R+h)² will be approximated by K/R² with an error of at most 2Kh/R³. Remembering such things as the gravitational constant, the mass and radius of the earth, we see that the error will be at most 0.000002h m/s². If we only need to calculate accurately to 2 decimal places, which is often more than enough, we can assume that aceleration due to gravity is constant provided h is less than 2500 m.

Population

Let's begin by mathematizing the original population model. We assume that over any fixed time period a constant fraction of the population will die, and a constant fraction of the population will be "born". The difference between "births" and deaths will give the relative population growth rate, which will be constant. Mathematically, if P is the population, P' its absolute growth rate, then the relative growth rate will be P'/P=k where k is constant. The only function satisfying this equation is the exponential function.

Since exponentials do not describe older populations very well, how do we adjust our model? According to Taylor's Theorem, changing the right-hand side of P'/P=k to a polynomial should work well, and the first polynomial we should try should be linear. Since we would really like the population growth rate to depend on the population itself rather than population and time (otherwise the same sized population will grow differently on January 1, 2000 and January 2, 2000), the right-hand side should be linear in P, or P'/P=k+CP where k and C are constants. Since the rate of increase should slow down as population rises, as P increases k+CP should decrease and C should be negative. Solving the resulting differential equation (you'll learn how to do this in integral calculus, or Math 1220) you end up with a logistic curve such as the one to the left of this paragraph. Notice that as t increases, the population approaches a fixed number, which is called the carrying population. Also notice that the rate of change of population slows, and approaches 0. Can you figure out what the carrying population is from the equation P'/P=k+CP?

While our arguments make sense from a mathematical point of view, there's no guarantee that bacterial populations really do follow a logistic curve. However, experimental evidence does support the logistic equation, at least for some range of t's.