Why are exponentials so important? Their primary importance used to be in calculations. In fact, until roughly 1970, if you wanted to multiply two numbers quickly, you used logarithms. Sextants and log tables used to be standard issue on ocean-going ships and slide rules really use a logarithmic scale to do multiplication. In fact, logs were so important for calculations that it was their use that established decimal notation.
Their importance for calculations came from changing multiplications, divisions and exponentiations into sums. To wit:
If you have ever had to multiply or divide many 3 digit numbers by hand, the usefulness of logarithms will be immediately apparent.
With the advent of calculators, the use of logarithms for calculations has all but disappeared. However, their use in data analysis is still strong, and depends largely on the three properties just mentioned.
First, a bit of a digression: if you believe that a particular data set describes a particular type of curve, say, exponential or polynomial, there are statistical techniques to find the "best" curve through your data. Unfortunately, finding the "best" curve of a particular type does not necessarily mean that you really have found the best curve: if you think a given data set is polynomial while it is actually exponential, you will have found the "best" wrong curve. The problem, then, is convincing yourself and your colleagues that you have found not only the "best" curve of a particular type, but the "right" type of curve as well.
On which data set would you be willing to stake your reputation?
 |  |
While the first data set "looks" parabolic (meaning y=Kx2), I wouldn't bet too much on it actually being so. The second data set clearly looks linear. I'd wager a lot more on it actually being so.
The idea, then, is to try to manipulate your given data set so that it looks linear. To see how logs can be used here, lets consider the following data set:

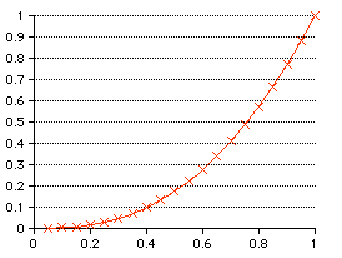
Suppose we believed it had the form y=Kxn. If we took logs, we would have log(y)=log(K)+nlog(x). If we plotted log(y) against log(x) we would get a straight line. Here is what we get in fact:
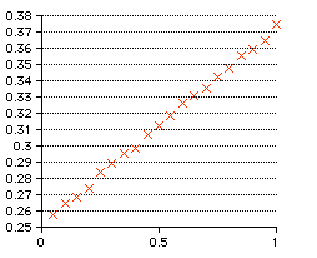
We might be able to fool ourselves into believing this is linear, but it would be hard to convince a non-believer. What if we thought it had the form y=Kax? Taking logs again, we would get log(y)=log(K)+log(a)x. Plotting log(y) against x would yield a straight line. We get in this case:
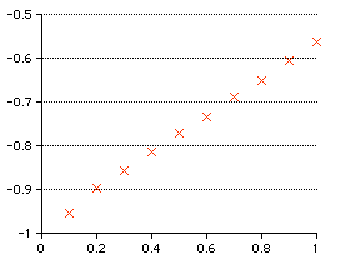
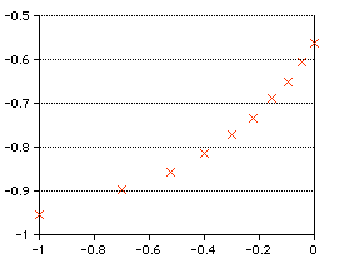
The graph finally looks linear. Our data set must have been exponential. Using stats we can find the line of best fit, which would give us log(a) and log(K), and hence a and K.
While much of what we have done may seem merely clever, it can save lots of time in data analysis. It took Kepler seven years to show his third law, which states that the square of the period of a planet's orbit is proportional to the cube of its mean radius from the sun (he was looking at our planetary system, of course). In other words, if T is the period and R the radius, T=KR3/2. Had he known of the use of logarithms in data analysis, he would have found this law in a matter of minutes. Before we condemn Kepler for stupidity, however, remember that he lived before Descartes revealed Cartesian coordinates, and before people thought of plotting data on a Cartesian plane. What we take for granted did not exist during Kepler's time.
| michaeln@kwantlen.bc.ca | Last modified: July 22, 2000 |