Effects of varying magnetic fields
 

Faraday's law of induction
 

Faraday's discovery in 1831 of the phenomenon of magnetic induction is one of the great milestones in the quest toward understanding and exploiting nature. Stated simply, Faraday found that (1) a changing magnetic field in a circuit induces an electromotive force in the circuit; and (2) the magnitude of the electromotive force equals the rate at which the flux of the magnetic field through the circuit changes. The flux is a measure of how much field penetrates through the circuit. The electromotive force is measured in volts and is represented by the equation
 

Here, , the flux of the vector field B through the circuit, measures how much of the field passes through the circuit. To illustrate the meaning of flux, imagine how much water from a steady rain will pass through a circular ring of area A. When the ring is placed parallel to the path of the water drops, no water passes through the ring. The maximum rate at which drops of rain pass through the ring occurs when the surface is perpendicular to the motion of the drops. The rate of water drops crossing the surface is the flux of the vector field v through that surface, where is the density of water drops and v represents the velocity of the water. Clearly, the angle between v and the surface is essential in determining the flux. To specify the orientation of the surface, a vector A is defined so that its magnitude is the surface area A in units of square metres and its direction is perpendicular to the surface. The rate at which raindrops pass through the surface is v cos A, where is the angle between v and A. Using vector notation, the flux is v A. For the magnetic field, the amount of flux through a small area represented by the vector dA is given by B dA. For a circuit consisting of a single turn of wire, adding the contributions from the entire surface that is surrounded by the wire gives the magnetic flux of equation (43 ). The rate of change of this flux is the induced electromotive force. The units of magnetic flux are webers, with one weber equaling one tesla per square metre. Finally, the minus sign in equation (43 ) indicates the direction of the induced electromotive force and hence of any induced current. The magnetic flux through the circuit generated by the induced current is in whatever direction will keep the total flux in the circuit from changing. The minus sign in equation (43 ) is an example of Lenz's law for magnetic systems. This law, deduced by the Russian-born physicist Heinrich Friedrich Emil Lenz, states that "what happens is that which opposes any change in the system."

Faraday's law is valid regardless of the process that causes the magnetic flux to change. It may be that a magnet is moved closer to a circuit or that a circuit is moved closer to a magnet. Figure 4

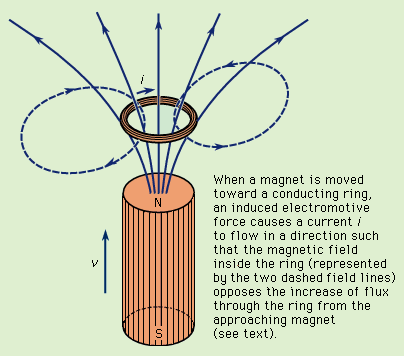
 Demonstration of Faraday's and Lenz's laws.shows a magnet brought near a conducting ring and gives the direction of the induced current and field, thus illustrating both Faraday's and Lenz's laws. Another alternative is that the circuit may change in size in a fixed external magnetic field or, as in the case of alternating-current generation, that the circuit may be a coil of conducting wire rotating in a magnetic field so that the flux varies sinusoidally in time.

The magnetic flux through a circuit has to be considered carefully in the application of Faraday's law given in equation (43 ). For example, if a circuit consists of a coil with five closely spaced turns and if is the magnetic flux through a single turn, then the value of for the five-turn circuit that must be used in Faraday's law is = 5. If the five turns are not the same size and closely spaced, the problem of determining can be quite complex.