EL TEOREMA DE LA TEORÍA POTENCIAL ELECTROSTÁTICA El problema plano en coordenadas cartesianas
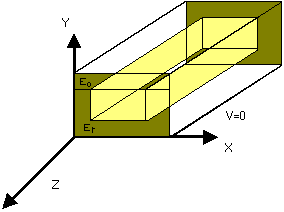
El problema es plano con respecto a la coordenada ¨Z¨. Es independiente de Z.
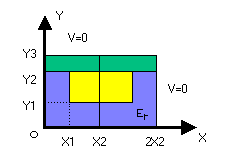
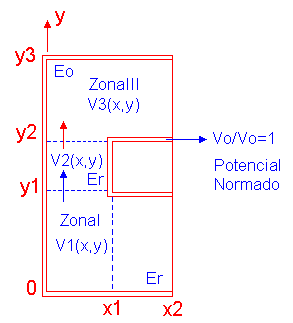
Dos constantes dieléctricas Er, Eo se separan en la superficie Y=Y2
El cilindro metálico interno está a un potencial V0
El cilindro externo está conectado a tierra V=0
La configuración es simétrica respecto a ¨ X2¨
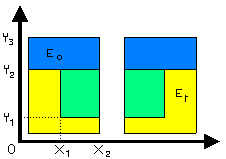
Gracias a la simetría, solo se resuelve la mitad del problema:
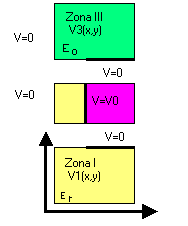
Se divide el problema en tres problemas parciales:
La configuración no contiene cargas dentro del cilindro.
Se debe determinar la solución de la ecuación de Laplace bidimensional para V(x,y)
Utilizando el artificio del producto V(x,y)=X(x)Y(y) se lleva a 2 ecuaciones diferenciales:
Llegando a las siguientes soluciones:
Xp(x)=ApCos(px)+BpSen(px)
X0(x)=A0+B0X
Yp(y)=CpCosh(py)+DpSenh(py)
Y0(y)=C0+D0Y
Determinar la solución de la Ecuación Diferencial de Laplace, implica sumar todas las soluciones anteriores para cada valor de ¨P¨
Para la solución de la Ecuación de Laplace:
DETERMINACIÓN DE LA SOLUCIÓN DE LA ECUACIÓN DE LAPLACE EN LA ZONA I
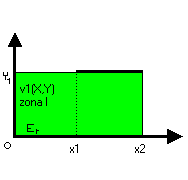
Condiciones de frontera homogénea:
Para Yc constante, V1(x2,yc) es igual a Vo.
cuando x = X2
Para X=0
® V1(0,y)Con la solución general de la ecuación de Laplace tenemos:
La solución de Laplace se simplifica ya que A0 = 0 y Ap= 0 y se obtiene:
1-2
Para Y=0
® V1(x,0) = 0Con la solución 1-2 se obtiene:
La solución de la ecuación 1-2 se simplifica, ya que B0C0 = 0 y Cp=0
Ap´ = BpDp 1-3
Para y constante, entonces:
Cuando x = X2
Con la solución 1-3 se obtiene:
B0D0 = 0 1-4
Se tiene la función Eigen:
Cos(pix2) = 0
y los valores Eigen:
pix2=ip -p /2
con i=1,2,3,4,5,6,7...
Simplificación del potencial 1-3:
1-5
Se norma al valor ¨V0¨ a V1:
V1(x,y) = V1(x,y)/V0
Determinación de la expresión matricial
Definición de Matrices:
El potencial: V1(x,y)= FT(x)senh[Py]A
DETERMINACION DE LA SOLUCION DEL POTENCIAL O ECUACION DE LAPLACE EN LA ZONA II
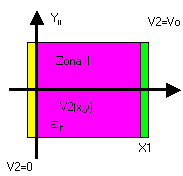
Desplazamiento de coordenadas
YII = Y-(Y1+Y2)/2 2-1
Condiciones de frontera homogénea:
cuando x = X1
La solución general de la Ecuación de Laplace es:
Con las condiciones de frontera 2-2 se tiene:
A0 = 0 y Aq = 0
El potencial:
Utilizando la condición de frontera:
se tiene:
B0D0 = 0 2-5
La función Eigen:
sen(qix1) = 0
teniendo como valores Eigen:
qixi = ip qi= ip /xi
Analizando la ultima condición de frontera se tiene:
V2(x1,YII) = V0
con 2-5
V0 = B0Cox1
B0C0 = V0/x1 2-6
El artificio del potencial:
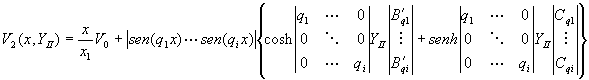
* GT(x) = Vector Transpuesto de sen(qix)
* Q = Matriz diagonal de qi
* B = Vector de constantes B´qi
* C = Vector de constantes Cqi
Se norma a V0
V2(x,YII) = V2(x,YII)/V0
ARTIFICIO DEL POTENCIAL EN LA ZONA III
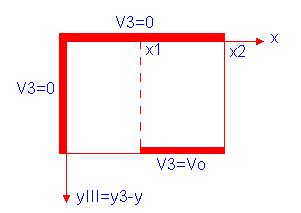
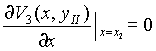
Condiciones de Frontera
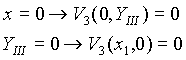(3-1)
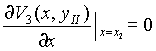
Soluciones de la Ecuación de Laplace
...
(3-2)
Para 
y 
El Potencial
(3-3)
El Potencial
(3-4)
C) Condición
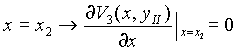
Con el potencial (3-4)
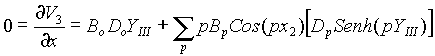
Función Eigen
(3-5)
Debe cumplirse
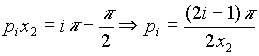
Valores Eigen
Para el potencial con (3-4)
(3-6)
Forma Matricial
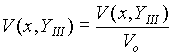
Valor Normado
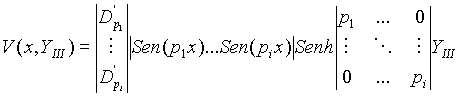
vector transpuesto de 
P = Matriz diagonal de 
D = Vector de constantes 
(3-7)
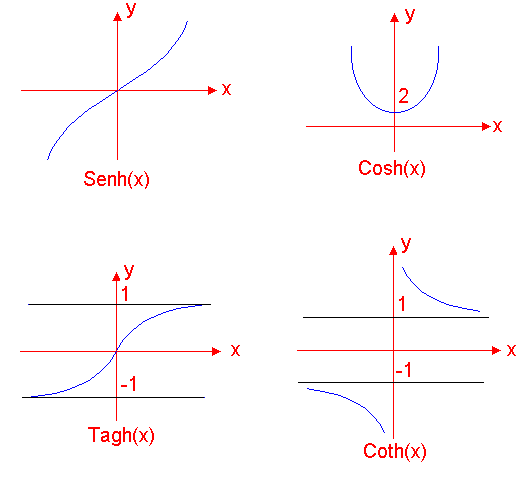
Los resultados de los potenciales se norman de manera tal que se obtengan tangentes y cotangentes hiperbolicas.
DETERMINACION DE LAS CONSTANTES
Zona I
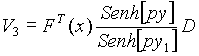
Zona II
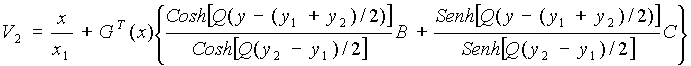
Zona III
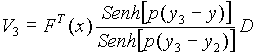
Para 
El flujo en dirección 
es continuo y constante en las superficies de contacto de las regiones I y II
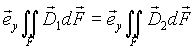
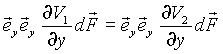
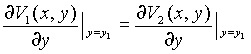
para 
(1)
Para 
el flujo normal a la superficie de contacto es continuo
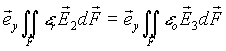
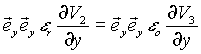
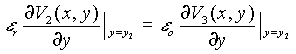
para (2)
El potencial es continuo
Para 
(3)
Para
(4)
Con las condiciones (1), (2), (3), (4) se aplican al sistema de los artificios de potencial. Se obtienen
Para 
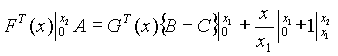
Para 0<= x <= X2
para
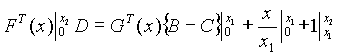
para x1 <= x <= X2 (5)
Se obtiene un sistema de cuatro (4) ecuaciones para las constantes A,B,C,D.
El sistema se simplifica aplicando conceptos de funciones ortogonales.
Se determinan matrices unitarias para simplificar el calculo.
----------------------------------------------
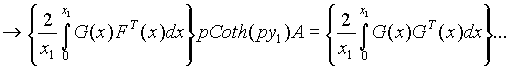
M-------------------------------------------------Matriz Unitaria
-----------------------------------
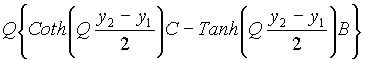
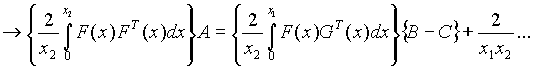
Matriz Unitaria-----------------------------MT
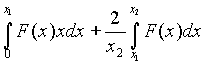
vector S
---------------------------------------
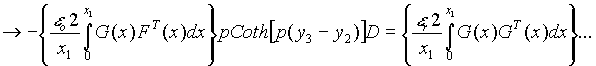
M--------------------------------------------------------------Matriz Unitaria
----------------------------------
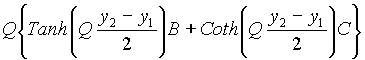
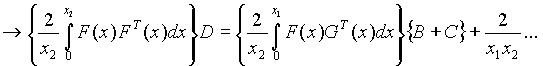
Matriz Unitaria-----------------------------MT
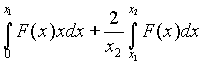(6)
vector S
Simplificación del sistema para A, B, C, D
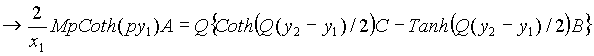
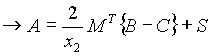
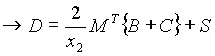(7)
CARACTERISTICAS Y ELEMENTOS DE LAS MATRICES
La matriz unitaria
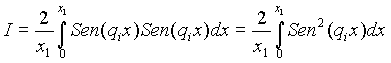
para 
para 
Para la matriz cuadrada M
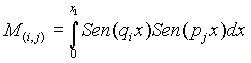
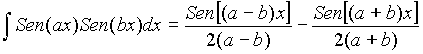
Para 
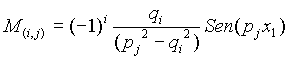
Para 
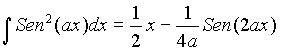
Forma General
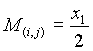
El vector S
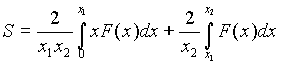
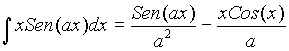
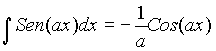
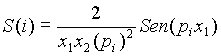
Simplificación de la representación matricial
Vectores
Va=A, Vb=B, Vc=C, Vd=DMatriz
Cuadrada Ma=MMatrices
diagonales Dp=P, Dq=Q,
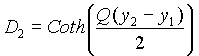
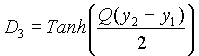
Constantes
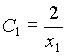
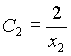
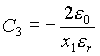
El Sistema
Sistema para Vc y Vb
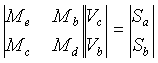
Vc y Vb se determinan por el método de Gauss
Ahora se procede a la determinación de las incógnitas y la graficación del potencial en el espacio bidimensional dentro del sistema.
[
PÁGINA PRINCIPAL] [SIGUIENTE][
CONOCIMIENTOS BÁSICOS] [PRINCIPIOS DEL CAMPO ELÉCTRICO ESTACIONARIO][
PRINCIPIOS DEL CAMPO MAGNÉTICO ESTACIONARIO] [LAS ECUACIONES DE MAXWELL][
POTENCIAL ELECTRODINÁMICO] [PROPAGACIÓN DE ONDAS]