CONDICIÓN DE ANÁLISIS DE LA PROPAGACIÓN DE LA ONDA PLANA El campo magnético de una onda plana es
H = ( x /m )½[ ez x E ]
Y de acuerdo a los resultados obtenidos en el análisis anterior, el campo magnético y el campo eléctrico son mútuamente perpendiculares entre sí y a la dirección de propagación.
Si, por ejemplo, se tiene que la forma del campo eléctrico y el campo magnético son respectivamente
E = ex E
H = ey H
Entonces, al sustituir en la expresión para el campo magnético, se obtiene lo siguiente:
ey H = ( x /m )½ E[ ez x ex ] Þ E / H = ( m / x )½
E / H es la relación de los campos, también conocida como la impedancia de onda, se representa con la letra Z y su unidad en el S.I. es el Ohm (W )
Z = E / H = ( m / x )½
En el vacío, la impedancia de onda se representa con
Z0 y su valor es de 120p W
La densidad superficial de potencia de la onda plana es
g
= E x H Þ g = E x ( x /m )½[ ez x E ] \ g = ez | E || H |
Con todos estos resultados es posible enumerar, para la onda plana, las siguientes características:
1.- Se propaga a la velocidad de fase V= (x m)-½.
2.- La relación entre los campos eléctrico y magnético se modela con la impedancia de onda
Z = (m/x)½.3.- La densidad de potencia se transporta en la dirección de propagación de la onda.
4.- La dirección de propagación la define el vector de Poynting el cual es normal al plano de onda. El plano de onda es un plano definido por el campo eléctrico y el campo magnético de la onda plana que a su vez son ortogonales.
5.- El módulo del vector de Poynting es el producto del módulo de los campos eléctrico y magnético.
CONSIDERACIÓN DEL POTENCIAL VECTORIAL ELECTRODINÁMICO ARMÓNICO
Recuérdese que
A(z,t) es un potencial vectorial libre de fuentes, es decir
div A(z,t) = 0
si se trata de una función armónica en el tiempo, entonces
A(z,t) = Â e{ A(z)ejwt }
La ecuación de onda para el potencial vectorial
A(z,t) es
![]()
tomando en cuenta que la propagación sólo se da en la dirección del eje
z, entonces, se obtiene la siguiente ecuación de onda armónica
¶
2¤ ¶z2 [A(z, t)] = ejwt D2z A(z) = w2m x A(z) ejwt
Donde
w2mx es el número o constante de onda y se representa con la letra griega b
b
= w2m x = w / V
por lo tanto, la ecuación de onda armónica puede expresarse de la siguiente forma
D2z A(z) = -b 2 A(z, t)
La solución general para esta ecuación, es la siguiente ecuación
A
(z, t) = A1 e-jb z + A2 ejb z
Si se trata de una función armónica en el tiempo y en el espacio
A
(z, t) = A1 ej(wt+b z) + A2 e-j(wt-b z)
donde el primer término del segundo miembro de la igualdad es la onda incidente y el segundo término es la onda reflejada. La cantidad
wt ± bz es la fase de la onda con w = 2p / T.
wt ± b z = wt ± (w / V)z = (2p / T)t ± (2p / TV)z = (2p / T)t ± (2p / l )z
|
|
||
|
frecuencia angular w = 2p / T |
número de onda b = 2p / l , l = TV |
|
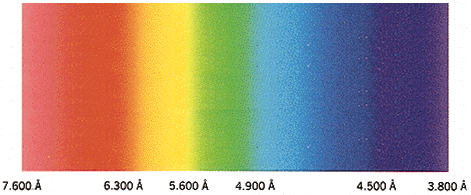
espectro de la luz visible cuya longitud de onda está comprendida entre 3.800 y 7.600 àngström (À)
[CONOCIMIENTOS BÁSICOS] [PRINCIPIOS DEL CAMPO ELÉCTRICO ESTACIONARIO]
[PRINCIPIOS DEL CAMPO MAGNÉTICO ESTACIONARIO] [LAS ECUACIONES DE MAXWELL]