MMU Egg Drop
Rules, Requirements, and Egg Information
- The container can be of any design, but may NOT include any of the following: Packaging materials (bubble wrap, styrofoam, peanuts etc), liquid or gases (other than air at atmospheric pressure), glass or ceramic materials.
- The empty container must have a mass of 500 grams or more.
- A raw large egg will be provided the day of the drop.
- The container must free-fall (no parachutes).
- The egg must survive intact (no cracks).
- The length shall be taken as the longest linear dimension of the complete container.
First, we sat down and created a concept for the drop.
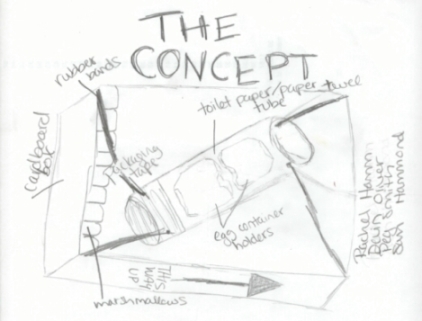
Next, we contructed our drop container from the following materials:
- Cardboard box
- Paper towel/cardboard roll
- Rubber bands
- Egg package pockets
- Marshmallows
- School glue
- Tape
- Toothpicks
- Dental floss
Then we put a raw egg into the drop container and tested it by dropping it out of a second story window.
and....

Data/Results:
Mass of container: 512.7 g
Mass of Egg: 66.1 g
Length: 31 cm
Time of fall: 1.07 s
Height from which box fell: 15 ft
EIF: 1.0
Drop zone score: 3
Final Score: 52,586.6
Analysis & Calculations
To convert our raw data into a score, we used this formula.
______10,000 contest points + DZ______ x EIF = SCORE
total mass(kg) x length(m) x time of fall (s)
- DZ is drop zone (where the egg landed)
- EIF is the Egg Integrity Factor (the state of the egg after the drop).
We found our DZ (drop zone) by matching the ring in which our box landed with it’s corresponding points. Our box landed in the third ring, so we received 500 DZ points. Our egg was intact after the collision, so our EIF was 1.0. From our data, the total mass was 578.8 g, or .5788 kg. The length was 31 cm, or .31 m. The time of fall was 1.07 s. This is what our equation looked like:
__10,000 + 500__ x 1 = 52586.6 = score
(.5788)(.31)(1.07)
So, our score was 52586.6. We also had to find the percent error of drop time. To find this, we used the formula observed – actual x 100. The observed time is our recorded time, which was 1.07 seconds. The actual time was given in class as .97 seconds.
So our equation was
1.07 - .97 x 100 = 10% error.
.97
Helpful Resources
How suspension absobs shock in cars
Suspension Bridges - Strongest Bridges Around
More Suspension Bridges
Egg drop concepts used by other groups
Fun Physics Game
Free Animated Words

View My Guestbook
Sign My Guestbook




