Release Action in Golf   -   myth versus real

Introduction

Let's first define release. The golf club during the forward swing describes two rotations. A primary one somewhere around the center of the shoulders and a secondary one relative to the wrists. Release is taken to be the secondary rotation adding angular speed to the primary one in the impact zone and henceforth causing the club to overtake the arms in the impact zone.

The intuitive approach towards release strongly suggested the centrifugal force as being the motivating force for the release action. It is probably for this reason that virtually everyone is on the wrong track. It is indeed paradoxical to consider the fact that centrifugal force is darned real, getting very large indeed, and yet playing no role in the release action of a golf swing.

In the mathematical analysis below we will use single, double and triple pendulums to analyze and illustrate forces and torques. To keep conceptually things as simple as possible we will use point masses, without losing the generality of the arguments. I feel that this makes it easier for most to more readily imagine where forces have their point of application and their line of action.

Why do we all, laymen, golfers, teachers and even some scientists, so strongly feel that it is centrifugal force being responsible for the release action of the golf club? It might in part come from the frequent illustration of the golf swing using the image of a small mass whirling at the end of a cord. One invokes frequently David slaying Goliath to convince the  student of the impressive power of centrifugal force. Also it is frequently mentioned that to be effective the center should move the least possible not to disturb the centrifugal force effect. Feeling the force pulling outward when whirling a small mass is indeed very convincing to make one believe in an outward centrifugal force acting on the clubhead, yet it is not true.

Even if we assume just for a moment that centrifugal force is indeed acting outwards on a whirling mass it is still totally inappropriate to compare a fast rotating particle to a golf swing. In golf the shoulders in the forward swing only rotate 90 degs starting from zero angular speed. Imagine a cord and stone and trying with minimal movement at the center to develop some peripheral speed through only 90 degs, starting from zero angular speed. In TGM this same error is also made in a different way when using the action of a gyroscope to discuss swing planes. Not only does the concept as used not apply, in addition the gyroscope is a fast rotating symmetrical device, very much unlike a golf forward swing which starts from zero speed, being asymmetrical and acting for only a very limited turn.

Part I   -   A closer look at centrifugal force

Centrifugal force, real or fictitious ?

It seems that many are, seemingly almost on purpose, trying to complexify the notion of centrifugal force. Some immediately invoke non-inertial reference frames and impress the laymen by invoking fictitious forces. However, golfers don't swing on dashboards of cars going through corners or facing a delicate approach shot the green standing on a merry go round. Then there are also those who claim that centrifugal force is not real but instead a fictitious force or some inherent feature of inertia.

Centrifugal force does not exist. Collins Concise Dictionary defines it as 'a fictitious force that can be thought of as acting outwards on any body that rotates or moves on a curved path'. The crucial word in that definition is fictitious. So why have we all heard of it? Indeed, why have we all felt it, on fairground rides, roundabouts and bicycles on corners?
....
So it is with centrifugal force.  Common sense and observation suggest that when standing on a playground roundabout, if you don' t hang on then some ' force' will throw you off. As is often the case, common sense is wrong. So what is going on?    

Quite common - Centrifugal force is mentioned not to exist and yet nevertheless somehow to have a definite action.
However, one can't have it both ways. It does exist and does not act outwards on a rotationg body.

Centrifugal force, a fictitious force, peculiar to a particle moving on a circular path, that has the same magnitude and dimensions as the force that keeps the particle on  its circular path (the     centripetal force) but points in the opposite direction.

The centrifugal force, as defined above, is not fictitious but is actually very real. It can be readily measured.

Centrifugal force is a virtual force. It is not really a force. There are some situations you can be in that have you accelerating without speeding up. One of these is a carnival ride that spins around in a circle at a constant speed. I know one where you feel pressed against the wall very tightly, and then the floor drops out.  

When moving fast, a great deal of force is required to make you change direction. Your body "wants" to continue in a straight line. The curved wall gets in the way. The wall pushes in against your body. The "outward force" is just your body trying to move in a straight line. It is not a force at all.  It is inertia, your body resisting the effects of the forces it feels.

This statement clearly is in conflict with Newton's third law. Here not only  centrifugal force is denied to exist but it is replaced by some mysterious innate characteristic of  inertia, which is a descriptive quality and not a force, does not have dimensions and can't be measured.  

Centrifugal Force is Not Real  -  A centrifugal force is the outward inertial force on an object moving along a curved path. It is not a real force but rather a fictitious or pseudo (false) force caused by inertia on the object. It is also sometimes called the centrifugal effect.

There are two basic errors:  
    1) The centrifugal force is not fictitious but instead very real indeed.
    2) Moreover one can't have a centrifugal and a centripetal force acting both on the same object - a mistake frequently encountered.

    
    

However, in general, the simple fact that centrifugal force is readily measured, as illustrated in Fig 5, should be sufficient to discard this quite common erroneous notion of centrifugal force to be not real, to be fictitious.

Golfers should not feel bad if they do not feel quite comfortably with all this mumbo jumbo with regard to centrifugal forces. Even some reputable golf scientists are not up to par and making fundamental mistakes with regard to centrifugal force.  

Centrifugal force in golf  

In golf instruction one likes to use the simple case of a small mass whirling around a center to demonstrate how the centrifugal force acts in golf swing. And here is where confusion starts. Simplifying is excellent but too much and it becomes very much counter productive. A lot of golf instruction is based on centrifugal force - Ernest Jones,  Manuel de La Torre, George Knudson, just to mention only a few.

George Knudson - 'The Natural Golf Swing'

Let's just quote from 'The Natural Golf Swing' by George Knudson - ("The man with the million dollar swing", Jack Nicklaus).

Centrifugal Force -  In its simplest terms, the centrifugal force is the outward force acting on a body that is rotating in a circle around a central point. . . . . .

Centrifugal force is powerful.  . . . . . It can generate clubhead speeds of more than hundred m.p.h. and gives the player a feeling of tremendous energy.

Here we see in a nutshell what is commonly believed / taught:  
    1) centrifugal force is acting outwards on the clubhead and
    2) powering the golf swing.  
Both assumptions however are not true.

If one let's slip somewhat the cord, indeed the whirling mass moves immediately away from you and one definitely feels a force pulling on the hands. Our intuition suggests strongly that there is hence a force acting on the rotating mass, pulling it away from us. This erroneous assumption, universally made in golf, is that this force is the reason why a club releases with such vigor in any descent golf swing in the impact zone.

First of all, there is no centrifugal force acting outwards on the clubhead. Moreover centripetal/centrifugal forces are central forces. Therefore, by definition, they can't do work as there is no lever arm to develop a torque. Hence centrifugal/centripetal forces can't be responsible for any type of release action of the club in the impact zone.

John Redman, 'Essentials Of The Golf Swing'

John Redman has a whole chapter on centrifugal force.  Summary given below:

Centrifugal force, in the special sense that I use the term, is the bedrock principle of good ball striking.
When applied to the swing, it provides everything - power, accuracy, and repeatability.
Centrifugal force is generated in the lower body with a hip turn and transmitted through the passive linkage of the arms and hands to the club head, where it takes the form of speed.
Its beneficial effects can be ruined by pushing on or applying pressure to the side of the club shaft with the hands and the arms.
To resist the instinctive urge to do that, think of the club as a rock tied to the end.

It is interesting to note that Redman mentions that his use of centrifugal force is technically inaccurate but that he uses it loosely as many others have done before him writing about golf. It is indeed difficult to eliminate the centrifugal force from the swing as it is so strongly agreeing with the way we feel the club acting through release. It reminds me of  Homer Kelley's approach who went yet one step further not believing that centrifugal force existed yet making its action the corner stone of swinging.

Don Trahan, Peak Performance Golf Swing

So, where does power come from?
Power comes from being able to swing your arms faster and more accurate on a straight line to impact and up to your finish.
It's all about moving your body less so you can swing your arms faster, creating centrifugal force, like swinging a rock on a string.
The faster the rock travels, the less the hand moves.  Your left arm, shaft and club head is the string and the rock.
The less your body turns (moves) the faster and more controlled you can swing your arms and club, and hit the ball more solid, straighter and longer.
But swinging in accord with physics of gravity and centrifugal force is less body and more arms to a ratio of arms 80 % and torso 20 %.
The less your body moves the faster and more controlled you can swing your arms.
And, if you want to get real consistant, the ratio will go to 90 % arms and 10 % torso.
This is the way I swing, my son, DJ, a PGA Tour player, swings and all my students swing.

Golf is a rather interesting kaleidoscope with many paradoxes. Don Trahan also is of the centrifugal force school of thinking, but rather contrasting with John Redman he wants a quite body and active arms and feels that in analogy with whirling stone, there should be the least amount of motion of the body possible.

Jim Dent & Rick Bradshaw, 'Centrifugal Golf Swing'

The cover illustration shows the common misconception about centrifugal/centripetal force. It's line of action is thought to pass through some swing center in the body. However it is not and it actually relates to the moving wrist joints. This means that, notwithstanding the very common belief in golf, there to be no centrifugal release torque acting on the club.

It is indeed no wonder that the average golfer gets confused. Golf scientists refer to centrifugal acceleration, centrifugal loading, centrifugal torque, centrifugal bending, centrifugal stiffening and hence implicitly suggesting that centrifugal force plays an important role in the golf swing.

Let's look at 'The Physics of Golf', by Jorgensen,  furthermore 'Search for the Perfect swing', the impressive early golf research effort, spear headed by Dr. Cochran and Staub, and also at  "The Tutelman Site", an interesting scientific golf web site.

Jorgensen,  'The Physics of Golf'

    page 179 / Technical Appendix - Section 9

Centrifugal Force

According to Newton's second law, the centripetal force on a body moving in a circle is proportional to the mass (weight) of a body multiplied by its centripetal acceleration. The centripetal acceleration increases with the radius of the circle on which it moves and with the square of the angular velocity of the motion. The centripetal force and the centrifugal force are not a third-law pair.

Surprisingly prof. Jorgensen states that centrifugal and centripetal force don't form a Newtonian action reaction pair of forces. Newton would not likely agree with this affirmation. A force can't exist in isolation. Forces come in pairs.

    page 178 / Technical Appendix - Section 9

Centrifugal Force

But when we ride on a merry-go-round we feel the force, we think, tending to throw us outward from the center. We look outward to see whether there is something out there pulling on us, and we find nothing of the kind. For all the forces we have considered so far there has been something to produce them. We have seen where the force of our weight, the force in lifting up a tea cup, and the force to pull a wagon come from. This force arises because we are riding on an accelerating  body, the merry-go-round. Such forces, for which we find no origin in objects such as ropes or rods and that do not produce accelerations in the direction of these forces are called by some 'pseudo forces", and this particular one is called a "centrifugal" force.

You may observe this centrifugal force if you place a golf ball on the surface just inside the windshield of your automobile and watch it roll from side to side as you drive around a curve. The ball always rolls to the outside of the curve and rolls more quickly the tighter the turn. Actually the ball does not accelerate, it appears to accelerate since there is no centripetal force to make it turn in the same path as the car. Its motion is the result of a lack of a centripetal force rather the result of an outward directed force being applied to the ball.

    page  182 / Technical Appendix - Section 9

Centrifugal Torque

Again consider a golfer riding on a merry-go-round. Let him somehow be prevented from being thrown off by the centrifugal force acting on him in the rotating system. Let him extend his arms and a golf club out along a radius from the axis of rotation. He feels no torque on the club because the lever arm of the centrifugal force on the head of the club is of zero length. Next let him hold the club so that his wrists are cocked at ninety degrees. There is still a centrifugal force in the rotating system on the clubhead out along a radius  from the axis. With this wrist cock, the centrifugal force will have a lever arm the length of the club.  The golfer riding in the rotating system will feel this torque, and without a matching torque on the club by the golfer, the club will start to move out to a greater radius. The torque on the club is thus a centrifugal torque. In the swing of a golf club, this is the torque that brings the clubhead out to the ball. This torque becomes very large.

I  am convinced that this kind of explanation, frequently used, is confusing for many. It does not sound quite proper as if someone is explaining some magic trick but not wanting to give away the real secret. However this stems from using, without any sound reason, inertial rotating reference frames. This definitely has its role in science to simplify calculations but has no role in explaining the dynamics of a golf swing. The casual reader will likely take it from 'The Physics of Golf' that release is caused by a centrifugal force / torque. However why use fictitious forces / torques when a simple Newtonian approach, hence involving REAL FORCES / TORQUES, is all that is required to analyze the release action of a golf swing.

Let's first analyze the example of a car going through a corner and having objects slide on the dashboard when going through a corner, Fig 6. For a nice demonstration we will rent a pickup truck with a nice large cargo area. Let's put some seats along both sides so that many can witness the experiment. Imagine a miniature ice rink mounted in the cargo area between the two rows of seats. The ice surface is ideal, no friction between it and the puck.

The invited people are all nicely seated and the pick up truck starts its run. First straight and cruising a steady speed. The puck is deposited on the ice just before the truck enters a curved section of the road and the fun starts. As shown in Figs 6 a to f, the puck just keeps going along a straight line relative to the road. The ice rink, attached to the cargo floor, curves with the pickup truck.

As there is no friction between the puck and the ice, there is no force exerted by it on the puck. It is here however that frequently one invokes centripetal and centrifugal forces, perhaps with some comments about how are senses are mystified, there being seemingly a force exerted on the puck as it moves relative to the ice rink. However there are no lateral forces, whatsoever, exerted on the puck.

But as soon as the puck hits an obstacle, such as the side board, then and only then, are REAL centripetal / centrifugal forces coming into play, Figs 6 g and h. If we had inserted a miniature compression scale between puck and board just before it making contact we would measure conveniently this real centrifugal force. There really is no need to invoke fictitious centrifugal forces and non-inertial rotating reference frames.

Let's next analyze Jorgensen's example, frequently used, of the merry-go-round, Figs 7a,b. Anyone not familiar with the subtleties of non inertial reference frames will likely take from this example that there is a 'real' centrifugal force acting on the clubhead acting outwards on the club head on an action line going trough the center of the rotation. It indeed fits our intuition quite nicely. The problem however is that normally a golfer does not swing a club standing on a merry-go-round, but instead simply on his two feet, solidly set onto mother earth. The merry-go-round is needlessly complexifying matters. It suggests the false notion that a real centrifugal force act outward on the clubhead and is responsible for its release action.

Jorgensen overlooked an important element. It is very important to know if the wrists are considered to behave like free joints. This is directly related to centrifugal force being a vector and the situation as given in Fig 7b is only true for the case when wrists are not considered to act like free joints, such as is the case for only a small portion, at the unset of the downswing. As soon as the wrists are the slightest amount free to move, the fictitious centrifugal force vector changes to a different alignment, as shown dotted in Fig 7b. When this is the case, the fictitious centrifugal force can't produce a torque acting on the club.

If we take the simple model as in Figs 8,a,b,c, by eliminating the merry-go-round away of Figa 7,a,b, then the only REAL external forces acting are the inner torque, wrist torque and gravity. Figs 8a,b,c  show the centripetal clubhead linear joint reaction force vector acting through the hinge. For the case depicted in Fig 8b one can have a substantial centripetal torque acting on the club, whereas there is zero centripetal torque for the case shown in Fig 8c.  

There is no real centrifugal force acting outwards on the clubhead. I admit that it is all very confusing because centrifugal force is definitely present, and actually quite large, but it is not an externally applied force, hence it can't do any work. However when only a sub part is considered in isolation one can think of linear joint reaction forces doing work. The overall effect of these joint reaction forces is however neutral, i.e., they don't generate net kinetic energy, only cause redistribution, as in a kinetic chain action.

Dr. Cochran et al , 'Search for the Perfect Swing'

    2:3 Why the upper lever slows down as the lower one speeds up.  Imagine the two-lever system lying static (i.e. not rotating) in the position indicated by the heavy lines. Then any force which pulls the head outwards will also tend to straighten the hinge out and move it 'backwards' as shown. Now think of the whole system rotating in the direction of the white arrow. The force pulling the head outwards is now centrifugal force; and the 'backward' movement of the hinge (due to its straightening out) is now superposed on the general forward rotation of the whole system, and so becomes merely a slowing down of the upper lever.

Fig 9 is a faithful redrawing of Fig 2:3 in  'Search for the Perfect Swing'. Contrary to Jorgensen there is no reference to non-inertial rotating reference frames and fictitious forces but still there are fundamental errors.

    1) There is no centrifugal force acting on the clubhead as shown.  There is instead only an inward directed centripetal force acting on the clubhead.

    2) The centrifugal/centripetal force is a vector and its line of action is definitely not as shown. Instead it line of action is through the clubhead and along the shaft.

The Tutelman Site

In the section,  "Applying Physics to Golf"  - "What powers the swing ?", there is the important question :
"What is creating that very strong rotation of the club about the hands, if the hands are not being used to supply a hit force ?"                     
and the answer given:
"The answer is centrifugal force".                           

We have here the same two basic errors as made by Cochran et al.

    1) There is no centrifugal force acting outwards as shown.  

    2) The line of action of any centrifugal/centripetal force is acting along the shaft of the club and not through the center of the shoulders.

Both Cochran et al, and Tutelman, consider the centrifugal force to be the source for the release action. This surely fits very well with our intuitive knowledge, but it is not correct.

Math vs Real

Scientists have contributed to this confusion. Some by immediately throwing at the poor confused golfer the notion of non-inertial reference frames which has no bearing on golf whatsoever. A golfer is simply not playing golf on the dashboard of a car going through a corner or on a merry-go-round. Others by kind of ignoring the existence of centrifugal force, uniquely mentioning the abstract notion, encountered in many text books, that an object circling around a center only requires a centripetal acceleration, Fig 10. However, in real life, such an object requires a real center force for either pulling or pushing on this circling object. Hence either a string or drum is required leading to centrifugal forces as the inevitable counter part of centripetal forces, Fig 11.
  

Inertial Forces

It is indeed very confusing for anyone trying to understand centrifugal force, even when consulting serious textbooks. The source of this confusion is perhaps due the ambiguous use in science of inertia and inertia(l) forces.

Inertial force is used in two different contexts.

    -1- As a force added to the equations of motion in a non-inertial reference frame to be able to use Newton's equations. It is then usually referred to as an pseudo or fictitious force.

    -2- The force produced by the reaction of a body to an accelerating force, equal in magnitude and opposite in direction to the accelerating force, d'Alembert's principle. An inertial force lasts only as long as the force does.

The problem is that frequently inertial forces are taken simply to be always fictitious, which is not true. This usage is rather puzzling as inertial forces are omnipresent and darned real. For instance when a bullet is being fired into your brain there are only inertial forces at work. It is indeed a pity that one can't witness after such an conclusive experiment that scientists should be more careful with their definitions.

Bumping into someone involve inertial forces. A tsunami, a hurricane, an earthquake, are rather impressive manifestations of inertial forces. So let's not just try to ignore them by assuming that they are just fictitious. Some scientists are so obsessed  with cause and action forces that they kind of ignore reaction forces and inertial forces and don't pay much attention to them.

The behavior of inertial forces is quite different from a force such as exerted by a spring. Inertial forces only exist for as long as there is motion. Moreover they don't have an agent acting on them. The force is simply there, i.e., it is not caused by any external agent.

Centrifugal force is a particular inertial force occurring whenever an object follows a curvilinear path; usually one refers to it in the context of a circular path. As mentioned for inertial forces in general happens also specifically for centrifugal force - centrifugal force is also used to indicate a fictitious force in non inertial rotating reference  frames. It it is also frequently considered to be only a fictitious force. Again not true. It depends.

The reason for existing confusion should therefore basically be a matter of semantics and nonchalant and incoherent use of definitions. But no, it goes much further. There are indeed those who strongly deny the existence of any real centrifugal force and at best consider it to be an inherent quality of inertia, hence contradicting Newton's third law. Others assume that centripetal and centrifugal force act on the same object, a fundamental error which is actually made quite frequently.

It took 2000 years to come to our present understanding of inertial forces and yet there is still much confusion. Through frequent exposure one might have the impression to understand inertial forces but they are indeed rather mysterious in nature.

Figs 12 a, b, c show the affinity between Newton's third law and d'Alembert's principle. Pushing against a wall or pushing against a movable object is really not very different. However in the first case one considers the reaction force F2 to be real and in the latter case as being a pseudo, apparent, or fictitious force. However if it walks like a duck and quacks like a duck, you can be reasonably sure it is a duck. It has the dimension of force, it behaves like a force, so why not consider it to be a real force.

Action and Reaction Forces

When dealing with multibody dynamics, as is the case with  a golfer, one has to be careful considering what exactly are the forces able to cause accelerations. These are the externally applied forces, being cause, and doing work. The reaction forces are effect and normally don't do work. However this depends on what we select as the system being analyzed. Reaction forces are important when looking at a particular segment of linked bodies, for instance, to determine joint forces or stress levels.

Forces always come in pairs. For every action force there is a reaction force, equal in magnitude and opposite in direction. This is effectively Newton's third law. The error frequently made is to assume that both forces do act on the same body. A surprising error since only superficial consideration would immediately lead to the conclusion that than they would cancel each other - still a common error. It is important to realize that action and reaction forces always operate on different bodies.

It is also important to realize that when two bodies, very different in size and mass, interact, the magnitude of the action and reaction force are nevertheless the same. Consequently the effect on the small body is substantial but almost negligible on the large body. People know this instinctively, when stepping out of a boat onto a deck. They are rather more careful when the boat is very small, but without any apprehension when the boat is rather large in size.

In golf, however, our intuition is playing games with us. Almost universally it is assumed that a centrifugal reaction force is acting outwards on the clubhead, whereas in reality it is actually a centripetal force which acts on the clubhead and pointing inwards not outwards. The centrifugal force is acting outwards from the wrist joints and acting along the shaft. Hence immediately it follows that release of the clubhead can't be caused by the centrifugal force, not acting on the clubhead or by a centrifugal torque as there is no lever arm for a torque to develop.

Centrifugal force in downswing

What causes release ?

Centrifugal force, by definition, is a central force. Hence such force can't develop a torque around its swing center, there being no lever arm. So we discard centrifugal force to play a significant role in release. Since everyone and everywhere in golf kingdom centrifugal force is taken to be the cause for release we better come up with something good to allow golfers still to release their club with confidence. So let's first give a general idea and then follow up with some more formal mathematical explanations.

Fig 13 shows the most elementary representation of a golf club, a point mass and a massless slender rod. The centrifugal force, in golf kingdom, erroneously, is assumed to act outwards from the point mass at A. Having eliminated this idea what is left? Well we have no choice and are forced to think about what might possibly happen at the other end, point B. Is it indeed feasible to fathom that the release torque might be developed at B ?

Point B represents the wrist joints of a golfer and, ignoring minor gravity and wrist torque contributions, there are no external torques acting at point B. So we are left with the  linear joint inertial reaction forces created by the interaction of bodies such as the arms and club. That is why I have included above some explanations of inertial forces and action reaction forces, being useful for understanding the true release mechanism.

We can produce some wrist torque at B but that is not sufficient to explain the release action. So what is left ? Moreover if I let go before impact and freewheel through impact where is the impetus for the obvious energetic release going on, being generated ? To get some idea we have to explain how torque can be generated at B by a linear force, not by an applied torque, and moreover we will have to invoke also the kinetic chain action.

From Figs 14 a,b it can be seen that a linear force applied at B is equivalent to a torque and a linear force.  The blue and red force, acting on the point mass in Figs 14 b, cancel. An elegant way to decompose a linear force into linear force and a torque with regard to center of mass.

The torque τ is positive when the point mass is above the horizontal but becomes a braking torque as soon as the point mass slips underneath the horizontal line. But there is a way to improve the situation. If we select a curvilinear trajectory for B as shown below we greatly improve on things.

Fig 16 shows the basic idea.  Whilst A starts to rotate, diminishing hence the angle θ  and therefore the torque, the force F, tracing the curvilinear path, is 'trying' to maintain some angle and hence a positive torque, as long as possible. Intuitively one can feel here the reason for the interest of Dr Nesbit, in his latest research efforts, for determining the optimum path for the hands. It also is related to Homer Kelley's endless belt effect, to 'pop the whip game' (Fig17), to shortening the swing radius, or equivalently, parametric acceleration.

When writing above, it made me think of Newton's cannon ball thought experiment (Fig18) - the ballistic problem of firing a canon ball at a certain angle and appropriate speed such that when the cannon ball starts falling back to earth, the earth just rotates away at the same rate with the consequence that the canon ball remains at constant height and behaves like a satellite, illustrated by path C. This problem has a bit of the same flavor as the curvilinear path of the hands to optimize torque.

Is invoking a linear force, acting along a suitable curvilinear path, sufficient to explain the vigorous release action felt by a golfer in the impact zone ? Or is there still more to it ? There is indeed. We have taken the club in isolation but in real life it is connected to the arms through hands/wrists. Very quickly in the down swing a rapidly increasing centripetal inward force is exerted through the arms/hands onto the handle. This the definite crux of the release issue. More on this below.

The beautiful free-wheeling action in the swing of a Bobby Jones through impact looks like there is no torque being exerted on the club since the golfer seemingly simply holds on. However that is a bit like the motion of a duck on water - all the vigorous activity beneath the surface is hidden from a casual onlooker. When the golfer lets go, there is a fairly large inertial torque at work making it appear like the golfer is just getting something for free.

Part II    -    release action  -  a mathematical analysis

In the analysis below we will use single, double and triple pendulums. To keep conceptually things as simple as possible we will use point masses, without losing the generality of the arguments. I feel that this makes it easier for most to more readily imagine where forces have their point of application and their line of action.  

It only pertains to 2D. However that is not essential in our case. Dr. Nesbit, even after having developed a very sophisticated 3D model, uses a 2D analysis in his recent paper,  ''Kinematic analyses of the golf swing hub path and its role in golfer/club kinetic transfers", as there is no point in going to 3D when it makes things needlessly complicated, with virtually no gain.

Governing differential equations

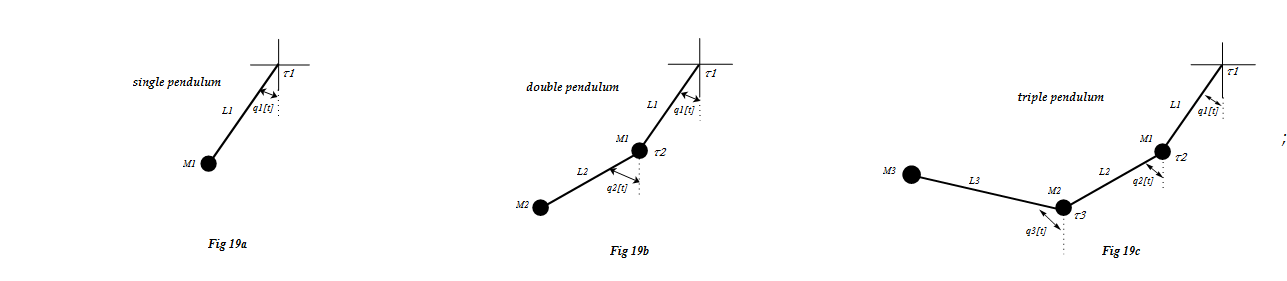
Single pendulum

Double pendulum

Triple pendulum

Notice that the differential equation for the single pendulum is very simple indeed when compared with the double pendulum and even more when compared to the triple pendulum equation.  We are moving away from the simple Newtonian mechanics of particles and getting a taste of multibody dynamics where non linear interactions start playing a very important role. We are still in 2D. When into 3D it is getting yet more complex.

External forces & torques

Single pendulum

Double pendulum

Triple pendulum  

Inertial joint reaction forces

Single pendulum

Double pendulum

Triple pendulum

Note -
Once the Fx, Fy components of the joint forces are known, one can then present the force vectors in various ways such as 1) cartesian  2) radial / tangential relative to trajectory and 3) projection on, and perpendicular relative to segments.

Solution of differential equations and joint reaction forces

Single pendulum

We consider the ensemble of point mass M and rod as a free body, Fig 22b. The motion of the mass is cause for a large joint reaction force at the center, which, however, can't do any work as no motion can occur. Hence the only forces remaining to consider are applied torque as centripetal/centrifugal forces don't come into play. They only cause some stress internal in the shaft.  

The relation between the angular position of the point mass M and the force vectors acting at the center is not evident in Figs 22a,b. To get a better feel let's consider the forces acting on the point mass M. These forces are respectively gravity, a constant tangential driving force and a reaction force, the latter acting at the interface of mass and rod. The top row, Fig23a to Fig26a, gives the force vectors whereas the bottom row, Fig23b to Fig26b, shows the corresponding torques.

The  Newton-Euler equation for the rotation of the point mass M, connected by a mass less rigid slender rod to a fixed center, is given by :
           
            M L q1"[t] = ∑(external torques + inertial torques).
            
The graphical presentation of the solution of this equation is shown above, where the graph in Fig 23b, is the sum of the remaining three graphs, Figs 24b,25b,26b.  

Note that the centripetal force, Fig24a, is very large but yet plays no role whatsoever in the motion of the mass M as it does not develop any torque relative to center, Fig24a. Also note that the centripetal force and the path are always at 90 degrees hence it can't do work and hence generate kinetic energy. Yet it is this rotating point mass example which is universally used to illustrate the action of the centrifugal force in the golf swing.

Double pendulum

External forces applied: torques τ1, τ2, respectively at center joint and hinge joint and gravity forces M1 g, M2 g. Torque τ1 is constant and the torque τ2 at the hinge is modeled to form a 90 degrees dead stop, preventing back knifing.  

Scrutiny of the governing differential equations (2) and (3) of the double pendulum show clearly that there is, even for such a simple two body system, already a complex non linear interaction taking place between the two segments, resulting in various inertial forces and torques. To more conveniently grasp the relative importance of the forces / torques acting on the 'wrist' joints, I have derived their magnitude / direction and presented these force vectors and associated torques in graphical form.

Figs 28a...33a  show the six forces acting at the wrist joints. Four inertial forces due to angular and radial acceleration of the two segments in addition due to gravity and wrist torque. Whereas Figs 28b...33b  show the corresponding torques resulting form these various forces acting at the wrist joints.

The Newton-Euler equation for the rotation of the outer segment, considered as a free body, is given by :   

     ∑ (external torques + inertial torques)

The 'b' graphs express this equation graphically :  M2 q2''[t] is given by the first graph, Fig 28b, and the 5 remaining ones, Figs 29b to 33b, are the various torques acting on the hinge joint. Hence the first is the sum of the five remaining.

The forces and torques are shown using the same scale to allow comparison. Notice that the joint force associated with the radial (centripetal) acceleration of the club, see Fig29a, is much larger than the other joint forces, and yet producing zero torque contributing to the release  action. This large force is usually and erroneously being taken as the centrifugal force acting outward on the clubhead.

The beauty of the graphical presentation of forces and torques is that it gives a clear instantaneous picture of the relative importance of the various joint forces during all of the down swing. It can be seen immediately that the release torque is generated almost exclusively by the radial (centripetal) acceleration of the arm, Figs 31a/b.

Some interesting conclusions can be drawn immediately.

    1) release torque is generated primarily by the radial acceleration of the arms.
    2) therefore, path of hands is important as radial acceleration is due to a curvilinear path, a circle in our analysis.
    3) furthermore, speed of hands is important as radial acceleration is proportional to hand speed squared.

The surprising fact for many will be probably that the very large centripetal acceleration of the club has no bearing on release. Usually and erroneously one takes this large force to be a centrifugal force acting out from the clubhead. Even admitting, for a brief moment, this to be true it still could not contribute to release as it is a vector aligned with the club shaft during release, and hence can't produce any release torque.

Let's look next at a triple pendulum and see what we can learn. In this case we are looking for a solution of the governing differential equations (4), (5) and (6) and the various wrist joint reaction forces embedded in equations (17) and (18), making up Fx3 and Fy3.

Triple pendulum

External forces applied: torques τ1, τ2, τ3, respectively at inner center, shoulder and wrist joint, and gravity forces M1 g, M2 g, M3 g. Torques τ1 and τ2 are taken constant and the torque τ3, at the wrist joint, is modeled to form a 90 degrees dead stop, preventing back knifing.  

We take the same approach as above for the double pendulum. We consider the distal element, the club, as a free body and consider all the torques acting on it to find out which might possibly contribute significantly to the release torque of the club in the impact zone.

First step required is the solve the differential equation (4), (5) and (6) and subsequently the solution used to derive the various joint reaction force vector elements making up Fx3 and Fy3, given by equations (17) and (18).

Scrutiny of the governing differential equations (4), (5) and (6) derived for the triple pendulum show clearly that there is a complex non linear interaction taking place between the three segments, resulting in various inertial forces and torques. We are specifically interested in the forces acting through the wrist joint as they are responsible for the release torque.

There are eight different forces acting through the wrist joint. To more conveniently grasp the relative importance of these forces / torques, I have derived their magnitude / direction and presented these force vectors and associated torques in graphical form below.

The six inertial forces acting on the wrist joint are associated with respectively the angular and radial acceleration of shoulders, arms and club segment, and this is indicated in the figures - e.g., 'arm / radial' refers to force/torque, at the wrist joint, due to radial acceleration of arms.  

The forces and torques are shown using the same scale to allow comparison. Notice that the joint force associated with the radial (centripetal) acceleration of the club, see Fig34a, is much larger than the other joint forces, and yet producing zero torque, contributing to the release action, Fig34b. This large force is usually and erroneously being taken as the centrifugal force acting outward on the clubhead.

The beauty of the graphical presentation of forces and torques is that it gives a clear instantaneous picture of the relative importance of the various joint forces during all of the down swing. It can be seen immediately, as for the double pendulum model, that the release torque is generated almost exclusively by the radial (centripetal) acceleration of the arm, Figs 38a/b.

The triple and double pendulums have for all practical purposes the same release behaviour for the club segment. As can be seen from the graphs the shoulder segment motion does not produce any significant force/torque at the wrist joint.

Conclusions

- Centrifugal force does not power the swing. Also it does not play a role in the release of the club through impact.
- The release is not caused by a centrifugal force acting through the clubhead but by a torque developed at the butt end of the club.
- The impetus for this release torque is generated primarily by the radial acceleration of the arms/hands.
- Swinging or hitting, the arguments above do apply.
  
  mandrin