Equilíbrio de forças coplanares sobre um ponto material

Diz-se que um ponto material está em equilíbrio quando a resultante das forças que atuam sobre ele é nula. Este equilíbrio pode ser estático ou cinemático. Será estático quando a velocidade do ponto for nula, e será cinemático quando a velocidade do ponto for diferente da nula e constante. Em nosso curso será comum nos referimos ao equilíbrio estático, apenas pelo uso do termo equilíbrio. Os casos que se tratarem do equilíbrio cinemático serão explicitados oportunamente.

O conceito de equilíbrio de forças em um ponto material geralmente é utilizado para determinar uma força incógnita, tal como uma reação de apoio ou uma força necessária para ``equilibrar'' esse ou aquele sistema de forças. Vejamos um exemplo analisando o problema exposto na Figura 2.4

Figure 2.4: Equilíbrio de forças em um poste

Neste problema, digamos que se queira determinar o valor da tração no cabo AB capaz de ``anular'' o efeito da força de 4500 N aplicada a direita do poste. Vamos reduzir esse sistema a um onde todas as forças envolvidas estão aplicadas em um único ponto, no caso, a origem dos eixos cartesianos apresentados na Figura 2.4 (atente para a orientação dos eixos !)

Para que a origem dos eixos esteja em equilibrio é necessário que a resultante das forças aplicadas naquele ponto seja nula. Sabemos ainda que podemos representar qualquer força através da soma vetorial das suas componentes cartesianas. Portanto, para o caso em estudo (forças coplanares) podemos representar a força resultante do seguinte modo:

$$\vec{R} = R_x \vec{i} + R_y \vec{j}$$ (2.1)

Para que a resultante da Equação 2.1 seja nula, é necessário que tanto $R_x$, quanto $R_y$ sejam nulos. Representando todas as forças envolvidas no sistema através de suas componentes cartesianas, podemos escrever que:

$$\begin{array}{c} R_x = \sum F_x = 0\\ R_y = \sum F_y = 0\\ \end{array}$$ (2.2)

Onde os $n$ termos em $F_x$ correspondem as componentes cartesianas, em relação ao eixo $x$, das $n$ forças do sistema e do mesmo modo os $n$ termos em $F_y$ correspondem as componentes cartesianas, em relação ao eixo $y$, das $n$ forças do sistema.

Nesse porblema temos duas forças: uma força $\vec{F}$ de intensidade igual 4500 N e outra força $\vec{T}$ cuja intensidade desconhecida nominaremos pela letra T (sem a setinha em cima). Representando as forças envolvidas em termos de suas componentes cartesianas teremos que:

$$\bgroup\color{black} \begin{array}{ccl} \vec{F} &=& (4500 \t... ...} + (T_y \times \, cos \, 14,03) \vec{j} \\ \end{array}\egroup$$

Fazendo com que o somatório das $n$ componentes na direção $x$ sejam nulos teremos que:

$$\bgroup\color{black} (4500 \times \, cos \, 30) - (T_x \times \, sen \, 14,03) = 0 \egroup$$

Procedendo igualmente em relação a direção $y$ teremos que:

$$\bgroup\color{black} - (4500 \times \, sen \, 30) + (T_y \times \, cos \, 14,03) = 0 \egroup$$

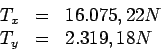
Uma vez que o sistema está em equilíbrio

$$\bgroup\color{black} \begin{array}{ccl} T_x &=& 16.075,22 N \\ T_y &=& 2.319,18 N \\ \end{array}\egroup$$

Portanto podemos escrever que:

$$\bgroup\color{black} \vec{T} = - 16.075,22 \vec{i} + 2.319,18 \vec{j} \egroup$$

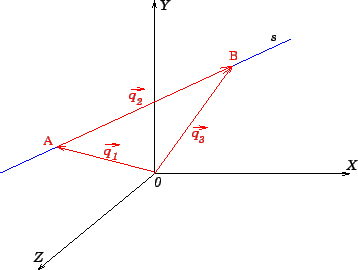
Desse modo, para determinar a intensidade da tração no cabo AB basta calcular o módulo do vetor $\vec{T}$. Assim, teremos que:

$$\bgroup\color{black} T = \sqrt{(16.075,22)^2+(2.319,18)^2} = 16.241,65 N \egroup$$

Pergunta: se ao invés de fixar o ponto de apoio A a 3 metros do poste, o fixácemos a 6 metros, para quanto iria a tensão no cabo AB ?

Antes de seguir adiante, outra pergunta: O que acontece quando multiplicamos o módulo de um vetor pelos seus cossenos diretores ?