All About Audio Amplifiers

Understanding the Transformer

Transformers are used largely in one place in an audio amplifier. It is in the power supply. Some rare circuits use transformers to couple the audio signal from the driver transistors to the outputs. To understand amplifiers you must under stand the workings of a transformer. The following is an excerpt taken from a textbook I wrote for the electronics course I used to teach. I have supplemented it with additional explanation and comments appropriate to the context of the internet. If you don't have a mathematical background just skip over the equations and look to the words where I will explain what is going on.

2.11 Transformers

A transformer is a device which will change the voltage and current of AC, but not DC. A transformer can be used to step down the voltage of the power line for use by circuits which would be damaged by the full 120 volts of the power line or step up the voltage for circuits which need higher voltage. In addition the electric utility itself uses transformers to step the voltage up and thereby step the current down to minimize the power lost in long power lines.



Figure 2.24 Schematic symbol for a transformer.

A transformer consists of two or more coils of wire wound on an iron core. The coils are usually wound one surrounding the other. The schematic symbol for a transformer is shown in Figure 2.24 above. The winding to which power is applied is called the primary winding and the winding from which the power is taken is called the secondary winding. Many transformers have more than two windings.

To determine quantitatively how the voltage is changed by a transformer we must remember the equation

e = n d fee d t. equation 2.41.

where E is the voltage across the coil, N is the number of turns on the coil and phi is the magnetic flux linking the coil. For the two windings of a transformer we can write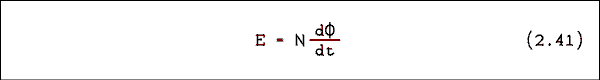

e sub p = n sub p d fee sub p d t, and, e sub s = n sub s d fee sub s d t. equation 2.42.

where the subscript P refers to the primary and the subscript S refers to the secondary. In a transformer the magnetic flux is so well confined by the iron core that all of the flux from the primary also links the secondary and visa versa. This means that Phi sub P = Phi sub S. We can divide equation 2.42a through by NP and equation 2.42b by NS which solves them for d Phi / dt, set them equal and rearrange terms to obtain the following equation.

e sub p over e sub s = n sub p over n sub s. equation 2.43.

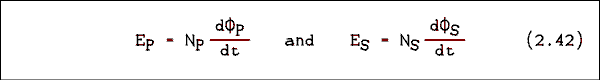Think of it as volts per turn. If a transformer had 600 turns on its primary the volts/turn would be 120/600 = 0.2 volts/turn. If a secondary on that transformer had 63 turns its voltage would be 63 x 0.2 = 12.6 volts. If another secondary winding had 2250 turns the voltage on this secondary would be 2250 x 0.2 = 450 volts.

Example 2.23

A transformer has 2450 turns on its primary and 700 turns on its secondary. If 120 volts is applied to the primary, what is the secondary voltage?

Solution:

The secondary voltage is

Es = Ep (Ns)/Np) = 120 (700)/(2450) = 34.29 vAC

Example 2.24

In the case of the transformer from example 2.23 if the secondary current is 850 mA, what is the primary current?

Solution:

Transformers are so good that the efficiency may be taken as 100% without introducing serious errors. Therefore, the power in the secondary equals the power in the primary. PP = PS and EP IP = ES IS; therefore,

i sub p over i sub s = e sub s over e sub p. equation 2.44.

and so IP = 850 mA x ( 34.29 v / 120 v ) = 243 mA.

From equation 2.44 you might deduce that

i sub p over i sub s = n sub s over n sub p. equation 2.45.

and you would be right.

A transformer which steps up the voltage will step down the current and vise versa. An electric utility uses transformers to step up the voltage to a very high value (as much as 300 kV) to send power over very long distances. When the voltage is stepped up, the current is stepped down. Most of the loss in power transmission lines is due to the resistances of the wires. Making the current as small as possible will minimize the power loss due to resistance. The voltage is stepped back down for distribution around cities and stepped down again just before being delivered to the customer.

Impedance Transformation (Output Transformer)

A note about terminology

The term "impedance" is often used when the term resistance could be applied. This is correct usage because of the way in which impedance is defined. Impedance is a combination of resistance and reactance (the effect of inductance and capacitance). The reactive component may or may not be zero. In the case of pure resistance it is still correct to say "impedance" even though there is no inductance or capacitance. Therefore, it is possible to say "impedance" and mean "resistance". The reverse of this is not true.

The apparent impedance of the primary of a transformer is given by ZP = EP / IP and the impedance in the secondary is ZS = ES / IS. If we divide equation 2.43 by equation 2.45 and solve the result for EP / IP we have

z sub p = e sub p over i sub p = e sub s over i sub s times quantity n sub p over n sub s close quantity over the quantity n sub s over n sub p close quantity. Carrying out the division on the right and substituting z sub s gives z sub p = z sub s times the quantity n sub p over n sub s quantity squared. equation 2.46.

Think of it this way, suppose we have a step down transformer. That's one that steps the voltage down. It also steps the current up. If the voltage was stepped down but the current remained the same the resistance would be stepped down. R = V / I. If the current were stepped up and the voltage stayed the same the resistance would also be stepped down. Since the voltage is stepped down at the same time that the current is being stepped up the resistance is stepped down twice. So the resistance (impedance) changes as the square of the turns ratio.

Example 2.25

What is the turns ratio of a transformer to match a 100 ohm base circuit to the collector of a transistor having an impedance of 3,000 ohms?

Solution:

Since power goes to the base, the 100 ohm side is the secondary of the transformer. The power flows from the transformer to the base of the transistor.

n sub p over n sub s = the square root of z sub p over z sub s close square root = square root of three thousand over 100 = 5.477.

Even though turns can only be whole numbers the decimal fraction doesn't matter. The manufacturer will use numbers large enough to come within 1 or 2 percent of 5.477.

Home

Or use your "Back" button to return to where you were.


Thank you for visiting my page at Angelfire.
Please come back and visit again!

This site begun July 27, 2006.

This page last updated July 31, 2006.