Abstract : The postulate of special relativity is reviewed.

I INTRODUCTION .

In his now famous work published in the year 1905 in the Annalen der Physik , Albert Einstein set the background for modern physical theories, stating two postulates which are the basis of the theory of Special Relativity : the first regarding the covariant form of laws of physics and the second which refers to the fact that the speed of light is constant for all observers situated in an inertial reference frame.

To give form to these two ideas, the concept of space-time is born together with the use of the Lorentz transformations of four dimensional vectors ensuring the second postulate.

In the structure of the Lorentz transformations there is a built in limit for the relative speed given between two inertial frames , the well known fact that no material object can go faster than light not even at the speed of light.

This third fact is derived from the structure of the Lorentz transformations, it is not a consequence of the two postulates of the Special Relativity theory, it is the purpose of this work to demonstrate that the built in limit given by the Lorentz transformations is a special case of a general set of transformations which are compatible with the Einstein Special Relativity postulates and with the quantum principle.

II GENERALIZED QUANTUM LORENTZ TRANSFORMATIONS

First postulate Special Relativity Generalized :

The speed of the light is constant for any observer regardless of their relative speed in a given quantum state labeled by a quantum number in the transformation law.

This postulate leads to the following set of transformations :

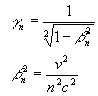
which leads to the following invariance :

in accordance with the Special Relativity postulate.

Note that for n=1 the usual Lorentz transformations are recovered with the usual speed light limit defining therefore the light cone as it has been known.

Therefore for quantum states in which n > 1 processes at the speed of light or higher are allowed and the Lorentz limit for the speed in the relative state is:

III QUANTUM LORENTZ CONTRACTION

The terms appearing in the transformation law:

can be interpreted as a quantum contraction factor for time and space respectively.

The question is how far can quantum contraction goes?.

If quantums of space and time are assumed:

They should stand for quantum contraction limits :

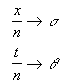
therefore forbidding infinite densities to occur.

IV QUANTUM METRIC

Given the Lorentz element labeled by quantum number n :

the space time metric can be defined as :

therefore Einstein equations become :

for n=1 the Quantum Lorentz invariance of Einstein equations set the General Relativity as usual .

V QUANTUM VACUUM STATES

The Einstein equations for the vacuum now read:

therefore for different values of n they point at different vacua structure, allowing a multiplicity of the classical vacuum described by .

The usual cosmological term corresponds to the first term of a source series defining the true global vacuum:

This series will be analysed in a future work.

Therefore the quantum number n reflects the structure of the global vacuum as a superposition of multiple vacua described by the series , setting the equations covariance level according to Lorentz covariance transformations . Each vacuum state is defined by :

where is in principle an arbitrary constant and n is a winding number labeling each vacuum state defined by

with

hence such number acts as the quantum number labeling the light cone defined by Lorentz transformations .

Given a multiple vacuum structure the global vacuum becomes:

where each represents a cosmological value.

Lets define the transition operator :

which shifts by one the vacuum state and spans the vacua set defining the transluminic spectrum for

n > 1 values.

VI CONCLUSIONS

General and Special relativity and physics derived from remain unchanged for n=1. In this case black holes form , no superluminal processes are allowed and quantum paradoxes stand such as the EPR paradox. In any case speed of light induced singularities associated to Lorentz invariance are removed for any

quantum state n by shifting over the vacuum structure.

So far high energy experiments confirm n=1 Lorentz invariance however, higher n Lorentz invariance phenomena should be confirmed by experimental physics according to the transformation laws given above.

Lorentz invariance of General relativity for n > 1 vacuum structure,allows superluminal processes ocurring in space-time therefore the black holes are not black in this context, and singularities may not occur due to the possibility of emission of large amounts of matter. Apparent quantum paradoxes can be resolved using this level of covariance.

Prejudice against faster than light processes derived from the original Lorentz transformations should leave place for a wider comprehension of the laws of the universe, recalling Galileo Galilei when he said: and yet it moves.

The author acknowledges the valuable help of G. Torres .

REFERENCES : A.Einstein , Annalen der Physik 18 (1905), p891