The Victor Orthophonic System:
The Maxfield-Harrison Electro-Mechanical Model (simplified)
Maxfield-Harrison Electro-Mechanical Table of Correspondences
| Force (dynes)
Velocity (cm/Second) Displacement (cm) Impedance (dyne sec/cm) Resistance (dyne sec/cm)
Reactance (dyne sec/cm)
Mass (gms) Compliance (cm/dyne)
|
Electromotive Force (volts)
Current (amperes) Charge (coulombs) Impedance (ohms) Resistance (ohms)
Reactance (ohms)
Inductance (henries) Capacity (farads)
|
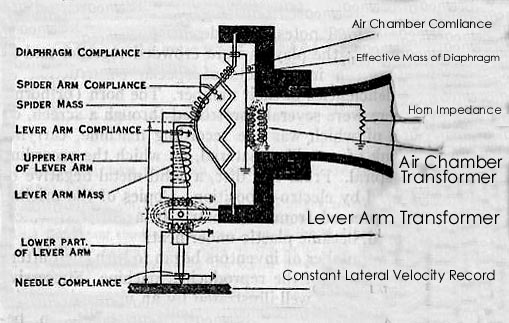
Figure 1
Compliance between two moving elements in direct connection is represented
as a shunt capacity; compliance between a moving element and a fixed or
rigid element in direct connection as a series capacity.

Figure 2
Simplified diagram of equivalents
Here are the two equations upon which the whole theory of design are based:
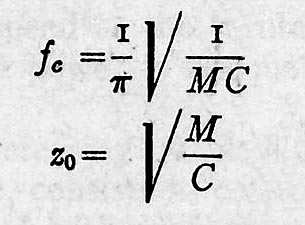
when...................
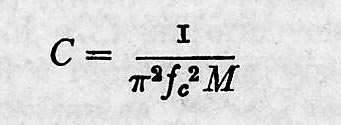
The record surface is to be considered an approximate equivalent of a constant current electrical generator of infinite impedance.
fc = transmission system cut-off frequency in cycles per second
C = shunt compliance per section in cm/dynes
M = series mass per section
zo = characteristic impedance over the largest portion of the band range.
(Confused yet?)
The value of M is a diaphragm of 13.5 cm sup 2 with a mass of .186 gms.
Cut-off frequency chose was 5,000 hz after which surface noise becomes a real nuisance.
In this particular example, the characteristic impedance is calculated @ 2920 mechanical ohms.
Maxfield and Harrison ultimately settled upon a final design that resulted in a characteristic impedance of about 4500 mechanical ohms to produce acceptable volume.
The lever-transformer ratio of 4500/2920 was determined as necessary to produce the required resistance in the system.
(I’ve talked to several engineers concerning the whole subject as it
pertains to the ‘Orthophonic’ system and all of them said it is tantamount
to a bunch of engineering voodoo and marketing mumbo-jumbo for the most
part.)
Page Created: 4 August 2003