This criterion specifies a shape that will tile the plane. In general the shape will be 2-anisohedral, though it is possible for it to be isohedral in some cases.

Start with a hexagon where opposite edges are 180° rotations of each other. In addition, two pairs of adjacent edges must be glide reflections of each other. The two edges that don’t participate in the glide reflection must be centro-symmetric. Here is my notation for such a shape and an example with the sides replaced by curves.

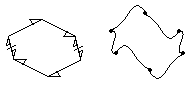
Note that such a hexagon will tile the plane (isohedrally.) It will do so in stripes of directly congruent shapes alternating with stripes of mirror images. Red and white would stand for opposite orientations.

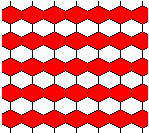
We will glue together multiple copies of the hexagon to create a more complex shape. Here are an example of how this might look. Each row must have the same number of hexagons as the next row with the same orientation – translating each hexagon perpendicular to the row.

In some cases the final shape has point symmetry. This allows us to cut it into two pieces using a centro-symmetric curve.

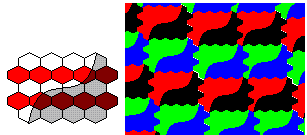
The first anisohedral tile, which was discovered by Heesch, fits this criterion:

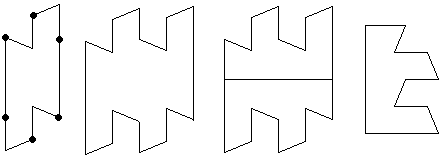
We have the shape on the left which is a hexagon type as mentioned above. We glue two copies of it together. By cutting it in half we obtain the tile desired. Here are some of the other published 2-anisohedral shapes that fit this criterion. I give the base hexagon shape, how I glue them together, and finally how you might cut it up.

Note that the last one has had the base hexagon collapse to a parallelogram by having the side edges collapse to nothing.

Back to anisohedral tilings page.