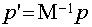Fractional to Orthonormal Coordinates Conversion Tutorial
This problem often comes up in crystallography where a unit cell is defined by a non-orthogonal basis (called fractional coordinates). Conversions between orthonormal and fractional coordinates have to be frequently performed. This describes one particular case of such transformation, where a is taken along x-axis and b lies in x-y plane.
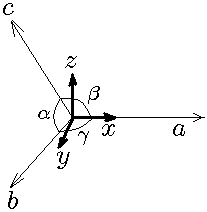
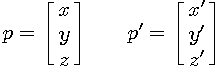
We want to transform point 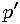 in fractional coordinates into orthonormal coordinates, producing point
in fractional coordinates into orthonormal coordinates, producing point 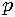 . Fractional coordinates are weights, linear combination of which with vectors
. Fractional coordinates are weights, linear combination of which with vectors 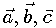 produces point
produces point 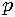 :
:
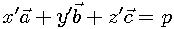
To carry out such transformation we have to multiply 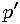 by
by  :
:
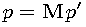
It is clear that  and
and 
First two coordinates of vector c are easily found using the dot product:


From which we find that: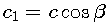

The third coordinate of c is found using the cross product:



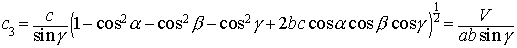
Where V is volume of the unit cell and is equal to:
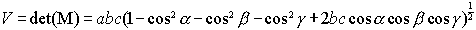
Finally the transformation matrix from 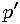 to
to 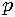 is:
is:

To carry out the inverse transformation from orthonormal to fractional coordinates we have to find the inverse of M:
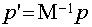
Inverse of M can be obtained from Cramer's rule:

From which we get:

Source Code
C++ source: class FracOrth for conversion between fractional and orthonormal coordinates: FracOrth.h FracOrth.cpp
Here is a dos program which does fractional to orthonormal coordinates conversion using the above class: frac.cpp

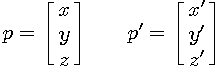
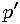 in fractional coordinates into orthonormal coordinates, producing point
in fractional coordinates into orthonormal coordinates, producing point 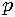 . Fractional coordinates are weights, linear combination of which with vectors
. Fractional coordinates are weights, linear combination of which with vectors 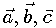 produces point
produces point 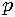 :
: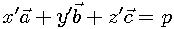
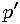 by
by  :
: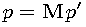
 and
and 


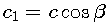




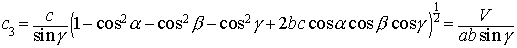
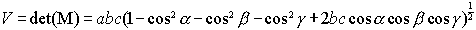
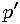 to
to 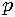 is:
is: