|

"Knowing the algorithm of this calculus, which I call differential calculus, we can find the maxima and minima as well as tangents
without the necessity of removing fractions, irrational, and other restrictions, as had to be done according to the methods that
have been published hithero."
Purpose
- To prove and explain these differntiation rules: the Constant Rule, the Power Rule, the Scalar Rule, and the Sum Rule.
Up to this point we have found derivatives by the limit difinition of the derivative. This procedure is rather tedious even for
simple functions, and fortunantly they are rules that greatly simplify the differentiation process. These rules permit us to calculate
the derivative without the direct use of the limits. We now derive some of these rules, and in each case we assume that the
derivative of the given function exits.
Constant Rule
The derivative of a constant is zero.

|
Proof
Let ƒ(x)=c; then by the limit definition
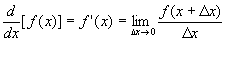

Power Rule

where n is any real number
|
Proof
Although the power rule I strue for any real number n, the binomial expansion applies only when n is
positive integer. Thus for the time being, we give a proof for the case when n is a positive integer.

Now applying the binomial expansion rule, we obtain

Scalar Multiple Rule

where c is a constant
|
Proof
Applying the limit definition,


Sum Rule
The derivative of the sum of functions is the sum of their derivatives.

|
Proof
Let F(x)=ƒ(x)+g(x). Then by the derivative of F is


          
| 