a Pb(N₃)₂ + b Cr(MnO₄)₂ ---->
c Pb₃O₄ + d NO + e Cr₂O₃ + f MnO₂
(16 ¾.¤. 45)

Find a, b, c, d, e, and f

a Pb(N₃)₂ + b Cr(MnO₄)₂ ----> c Pb₃O₄ + d NO + e Cr₂O₃ + f MnO₂

a = 15, b = 44, c = 5, d = 90, e = 22, f = 88

I do not use Oxidation Number Method krub.

I just balance no. of atoms for both sides.
And try to get integer solution krub.

Oxidation Number Method krub

There are many methods of achieving balanced equation (both atomic number and charge).

Oxidation-Reduction method is the most widely used because it can explain what happen chemically, my future kratoo will base the balancing on mathematical context alone krub.

With mathematical method, there will be no need for guessing (inspection technique) at all, we can extract the balancing number out of the unbalanced equation directly with the help of MATLAB and EXCEL program.

Mathematical method can be used to confirm whether the balancing set of number that we obtained from the conventional "reduction-oxidation" method is correct.

Let’s try another problem

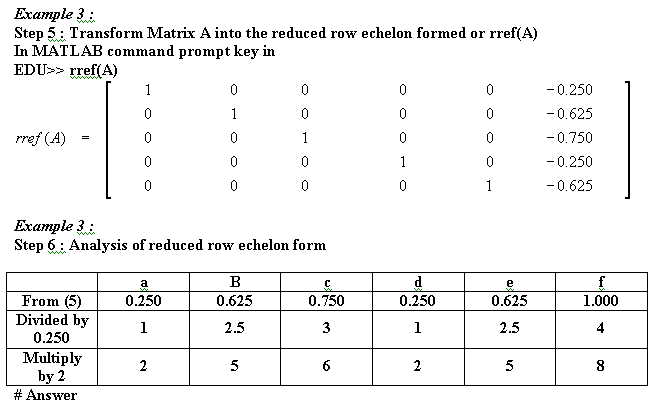
a MnO₄^- + b C₂O₄^-2 + c H₂O ---> d MnO₂ + e CO₂ + f OH^-

1. History of method development

You can skip this part krub ^ ^

The idea came up to my mind since I was in Grade 8 – 9 (junior high school, Mor 2 – 3) krub, at that time due to insufficient knowledge (oxidation/reduction half reactions). All I could do was balancing with inspection method. The linear equation system was just too complicate at that time (due to lack of knowledge in matrix algebra). However, for some complicate redox equations that consist of several atomic balancing equations, the early stage mathematical method can solve them easily as can be seen in kratoo above that khun eq0 solved it for us krub.

When I was in senior high (Mor 4 – 6), the principle of oxidation/reduction half reaction as well as matrix algebra concept were introduced. However, the software/computer hardware were still in early stage of their development (386 was considered the fastest PC). Producing reduced row echelon form (abbreviated as rref function in MATLAB 4.0) from original matrix “by hand” was not easier than the half reaction method.

In second year of my undergraduate in Chemical/Bioprocess Engineering, several matrix algebra computer programs were introduced such as MAPLE 6.0, MATLAB 4.0 – 6.0 and Turbo Pascal 7.0. I spent my winter holiday writing up the chemical balancing program using Turbo Pascal 7.0. “Infinite balancing set” was discovered (to be explained later).

Now, in my postgraduate year; my research works are still related to matrix manipulation but for non-linear regression modeling of microbial growth and enzyme kinetics krub. A few days ago I looked back to the unfinished work, this time I might be able to pin it down ^ ^.

2. What is this method ?

By convention in order to balance any redox equation, one needs to have knowledge of oxidation/reduction half-reaction. Without this knowledge, balancing the chemical reaction could be difficult {based on the inspection method (“trial and error”) alone}. This method utilizes the solving of linear equation systems with matrix algebra.

Two programs are used here ; MATLAB 4.0 Student Edition and EXCEL spreadsheet program (any version).

3. Who can use it ?

This is simply an alternative method for obtaining balanced coefficients for redox equations. It will be particularly useful for those who are studying/reviewing the method on how to balance the redox equation with half-reaction (to confirm the results). In the past, it is not so practical because few computers/programs are available.

4. Why do we bother considering this method ?

It is fast and accurate. Especially for complicate redox equation involving several chemical species. For those who have some experiences on balancing half-reaction. They will understand that there are many tedious steps and errors could be made easily. However, it is not my intention to encourage students using only mathematical method to balance the redox equation. The focus should still be on oxidation-reduction half reaction because there are other uses of half reaction in area of physical chemistry such as electrochemistry.

The discovery of “infinite balancing set” from mathematical method (you will not be able to use half reaction method to identify which redox reactions can have “infinite balancing set” krub, only mathematical method can identify it) proves that the original checking criteria of balanced charges and balanced atoms are not sufficient. The chemists should also investigate whether the summation of oxidation number (multiply with balancing coefficient) of the oxidizing/reducing agents on the left and right of redox equation are the same.

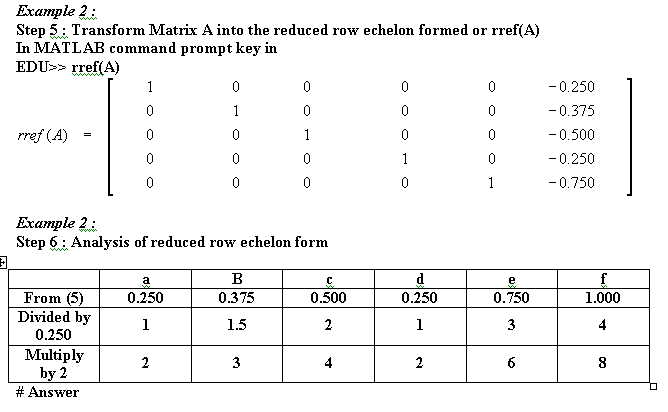
2 MnO₄^- + 7 H₂O₂ + 6 H⁺ ---> 2 Mn²⁺ + 6 O₂ + 10 H₂O…..(1)

2 MnO₄^- + 5 H₂O₂ + 6 H⁺ ---> 2 Mn²⁺ + 5 O₂ + 8 H₂O…..(2)

Both charges and atoms are balanced in (1) & (2) but

Summation of balanced oxidation number of (1) for Mn & O is
LHS = 2*(+7) + 7(-2) = 0
RHS = 2*(+2) + 6(0) = 4 since LHS <> RHS (1) is not right.

Summation of balanced oxidation number of (2) for Mn & O is
LHS = 2*(+7) + 5(-2) = 4
RHS = 2*(+2) + 6(0) = 4 since LHS = RHS (2) is correct.

5. When to use this method ?

To check the answer by independent method, if the balancing coefficients match, it is likely that the solution is correct.

When oxidation-reduction half reaction method does not produce valid results, use the mathematical method to recheck.

6. How to do it ?

µÑÇÍÂèҧ⨷Âì 1

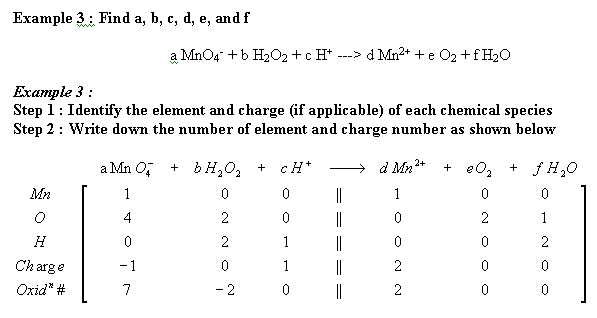
Other equations that has been balanced with mathematical method :

(1) a HNO₃ + b H₃PO₃ ---> c NO + d H₃PO₄ + e H₂O

(2) a Cr₂O₇^-2 + b H⁺ + c I^- ---> d Cr⁺³ + e I₂ + f H₂O

(3) a As₂O₃ + b H⁺ + c NO₃^- + d H₂O ---> e H₃AsO₄ + f NO

(4) a CuS + b NO₃^- + c H⁺ ----> d Cu⁺² + e NO₂ + f S + g H₂O

(5) a H₂SeO₃ + b Br^- + c H⁺ ----> d Se + e Br₂ + f H₂O

(6) a Fe⁺² + b Cr₂O₇^-2 + c H⁺ ----> d Fe⁺³ + e Cr⁺³ + f H₂O

(7) a HS^- + b IO₃^- + c H⁺ ---> d I^- + e S + f H₂O

(8) a CrO₄^-2 + b I^- + c H⁺ ---> d Cr⁺³ + e I₂ + f H₂O

(9) a IO₄^- + b I^- + c H⁺ ----> d I₂ + f H₂O

(10) a MnO₄^- + b H₂O₂ + c H⁺ ----> d Mn⁺² + e O₂ + f H₂O

(11) a H₃AsO₄ + b Zn + c H⁺ ----> d AsH₃ + e Zn⁺² + f H₂O

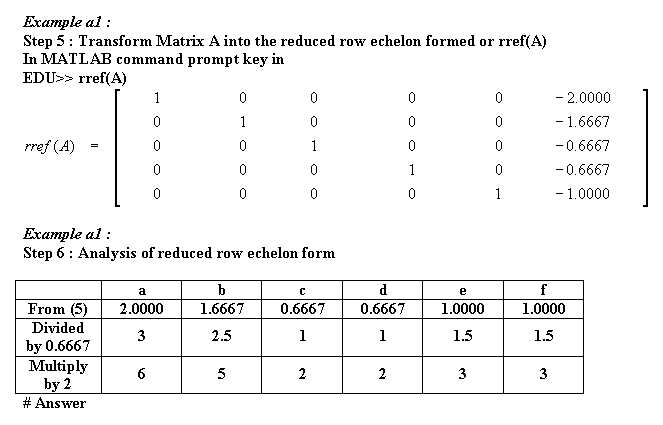
Example a1 : Determine a, b, c, d, e, and f from

a KNO₃ + b S + c H₂O ----> d H₂SO₄ + e N₂ + f K₂SO₄

Oxidation – Reduction half reaction method

1. Identify the oxidising and reducing agents ;

NO₃^- ----> N₂ ; Oxidation number of N is changed from +5 in nitrate ion to 0 in nitrogen, because nitrate gains electrons, it is oxidising agent.

S ----> SO₄^2- ; Oxidation number of S is changed from 0 in element sulfur to +6 in sulphate ion, because sulfur element loses electrons, it is reducing agent.

2. Balance element species which is not hydrogen or oxygen first ;

Reduction half reaction : 2NO₃^- ----> N₂

Oxidation half reaction : S ----> SO₄^2-

3. Balance oxygen in each half reaction with water ;

Reduction half reaction : 2NO₃^- ----> N₂ + 6H₂O

Oxidation half reaction : S + 4H₂O ----> SO₄^2-

4. Balance hydrogen in each half reaction with proton ;

Reduction half reaction : 2NO₃^- + 12H⁺ ----> N₂ + 6H₂O

Oxidation half reaction : S + 4H₂O ----> SO₄^2- + 8H⁺

5. Balance charge in each half reaction with electrons ;

Reduction half reaction : 2NO₃^- + 12H⁺ + 10e^- ----> N₂ + 6H₂O

Oxidation half reaction : S + 4H₂O ----> SO₄^2- + 8H⁺ + 6e^-

6. Combine Oxidation/Reduction half reaction together for construction of “Redox equation”

In order to do this, we have to find “Least common multiple (LCM)” or in Thai (Kor Ror Nor) of electron gained or lost. In this case LCM(10, 6) = 30

3 x Reduction half reaction : 6NO₃^- + 36H⁺ + 30e^- ----> 3N₂ + 18H₂O…..(1)

5 x Oxidation half reaction : 5S + 20H₂O ----> 5SO₄^2- + 40H⁺ + 30e^-….(2)

Redox equation : (1) + (2)

6NO₃^- + 36H⁺ + 30e^- + 5S + 20H₂O ----> 3N₂ + 18H₂O + 5SO₄^2- + 40H⁺ + 30e^-

Cancel out 30e^-
6NO₃^- + 36H⁺ + 5S + 20H₂O ----> 3N₂ + 18H₂O + 5SO₄^2- + 40H⁺

Subtract water from the left hand side of equation ;
6NO₃^- + 36H⁺ + 5S + 2H₂O ----> 3N₂ + 5SO₄^2- + 40H⁺

Subtract proton from the right hand side of equation ;
6NO₃^- + 5S + 2H₂O ----> 3N₂ + 5SO₄^2- + 4H⁺

Add in potassium ion and split 5 x sulphate ions into potassium sulphate and sulfuric acid as required by the question :
6KNO₃+ 5S + 2H₂O ----> 3N₂ + 3K₂SO₄ + 2H₂SO₄

Thus (a,b,c,d,e,f) is (6,5,2,2,3,3) # Ans

µÑÇÍÂèҧ⨷Âì a1

From the equation ;

a MnO4- + b H2O2 + c H+ ---> d Mn2+ + e O2 + f H2O

The following equations are all balanced ;

2 MnO4- + 3 H2O2 + 6 H+ ---> 2 Mn2+ + 4 O2 + 6 H2O

2 MnO4- + 1 H2O2 + 6 H+ ---> 2 Mn2+ + 3 O2 + 4 H2O

2 MnO4- + 7 H2O2 + 6 H+ ---> 2 Mn2+ + 6 O2 + 10 H2O

2 MnO4- + 11 H2O2 + 6 H+ ---> 2 Mn2+ + 8 O2 + 14 H2O

2 MnO4- + 5 H2O2 + 6 H+ ---> 2 Mn2+ + 5 O2 + 8 H2O

But how is this possible ? which one is correct ?

It's long times ago for me , a tutor. I choose this one 2 MnO4- + 5 H2O2 + 6 H+ ---> 2 Mn2+ + 5 O2 + 8 H2O is correct krub , calculated by balancing redox equation method.

Khun Halogen is correct. All of them are mathematically correct (that's why it is possible) but the last one is also chemically correct. Why? Because to solve this type of problems, one needs to consider which reactant is a reducing agent and which is an oxidizing agent. With that in mind, the only last equation contains the correct number of electrons transfered.