Cinemática

- Movimiento rectilíneo

- Posición

Cinemática

 

 

 

 

 

 

 

 

Movimiento rectilíneo

Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

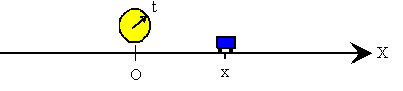
En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.

Posición

La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).

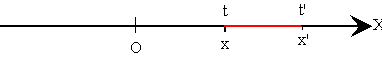
Desplazamiento

Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, que va desde el instante t al instante t'.

Velocidad

La velocidad media entre los instantes t y t' está definida por

Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero.

Pero dicho límite es la definición de derivada de x con respecto del tiempo t.

Aceleración

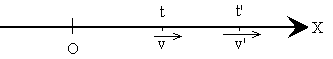
En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t.

La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que no es otra cosa que la definición de la derivada de v.

 

Dada la velocidad del móvil hallar el desplazamiento

Si conocemos un registro de la velocidad podemos calcular el desplazamiento x-x₀ del móvil entre los instantes t₀ y t, mediante la integral definida.

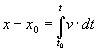
El producto v dt representa el desplazamiento del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes t₀ y t.

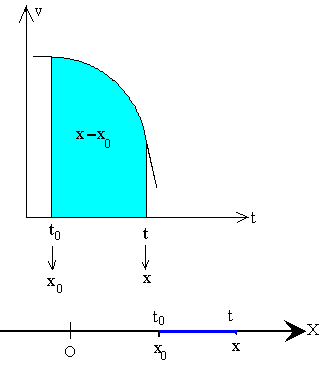En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t0 y t, el segmento en color azul marcado en la trayectoria recta. Hallamos la posición x del móvil en el instante t, sumando la posición inicial x0 al desplazamiento, calculado mediante la medida del área bajo la curva v-t o mediante cálculo de la integral definida en la fórmula anterior.

 

Dada la aceleración del móvil hallar el cambio de velocidad

Del mismo modo que hemos calculado el desplazamiento del móvil entre los instantes t₀ y t, a partir de un registro de la velocidad v en función del tiempo t, podemos calcular el cambio de velocidad v-v₀ que experimenta el móvil entre dichos instantes, a partir de un registro de la aceleración en función del tiempo.

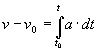
En la figura,  el cambio de velocidad v-v0 es el área bajo la curva a-t, o el valor numérico de la integral definida en la fórmula anterior. Conociendo el cambio de velocidad v-v0, y el valor inicial v0 en el instante t0, podemos calcular la velocidad v en el instante t.

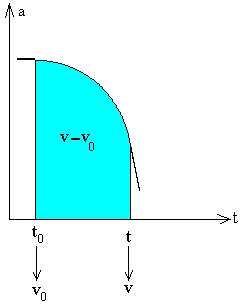
Resumiendo, las fórmulas empleadas para resolver problemas de movimiento rectilíneo son

 

Movimiento rectilíneo uniforme

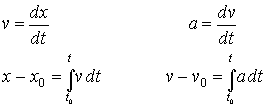
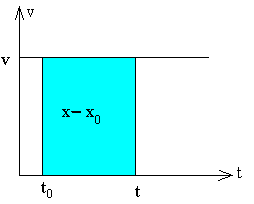Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando o gráficamente, en la representación de v en función de t.

Habitualmente, el instante inicial t₀ se toma como cero, por lo que las ecuaciones del movimiento uniforme resultan

 

Movimiento rectilíneo uniformemente acelerado

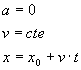
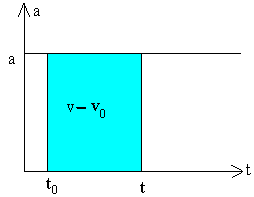	Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v0 entre los instantes t0 y t, mediante integración, o gráficamente.
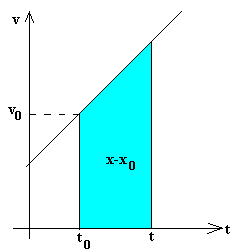	Dada la velocidad en función del tiempo, obtenemos el desplazamiento x-x0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

Habitualmente, el instante inicial t₀ se toma como cero, quedando las fórmulas del movimiento rectilíneo uniformemente acelerado más simplificadas.

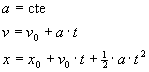
Despejando el tiempo t en la segunda ecuación  y sustituyéndola en la tercera, relacionamos la velocidad v con el desplazamiento x-x₀

 

Movimiento Circular

En esta sección vamos a definir las magnitudes características de un movimiento circular, análogas a las ya definidas para el movimiento rectilíneo.

Se define movimiento circular como aquél cuya trayectoria es una circunferencia. Una vez situado el origen O de ángulos describimos el movimiento circular mediante las siguientes magnitudes.

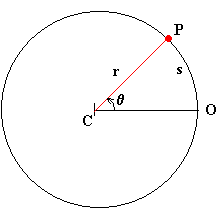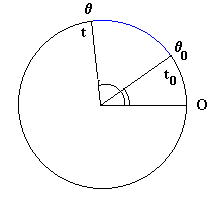
Posición angular, q En el instante t el móvil se encuentra en el punto P. Su posición angular viene dada por el ángulo q, que hace el punto P, el centro de la circunferencia C y el origen de ángulos O. El ángulo q, es el cociente entre la longitud del arco s y el radio de la circunferencia r, q=s/r. La posición angular es el cociente entre dos longitudes y por tanto, no tiene dimensiones.

Velocidad angular, w

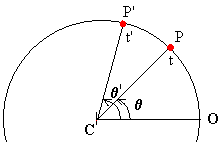En el instante t' el móvil se encontrará en la posición P' dada por el ángulo q '. El móvil se habrá desplazado Dq=q ' -q en el intervalo de tiempo Dt=t'-t comprendido entre t y t'.

Se denomina velocidad angular media al cociente entre le desplazamiento y el tiempo.

Como ya se explicó en el movimiento rectilíneo, la velocidad angular en un instante se obtiene calculando la velocidad angular media en un intervalo de tiempo que tiende a cero.

Aceleración angular, a

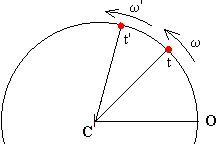Si en el instante t la velocidad angular del móvil es w y en el instante t' la velocidad angular del móvil es w'. La velocidad angular del móvil ha cambiado Dw=w' -w en el intervalo de tiempo Dt=t'-t comprendido entre t y t'.

Se denomina aceleración angular media al cociente entre el cambio de velocidad angular y el intervalo de tiempo que tarda en efectuar dicho cambio.

La aceleración angular en un instante, se obtiene calculando la aceleración angular media en un intervalo de tiempo que tiende a cero.

Dada la velocidad angular, hallar el desplazamiento angular

Si conocemos un registro de la velocidad angular del móvil podemos calcular su desplazamiento q -q₀   entre los instantes t₀ y t, mediante la integral definida.

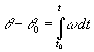
El producto w dt representa el desplazamiento angular del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos angulares infinitesimales entre los instantes t₀ y t.

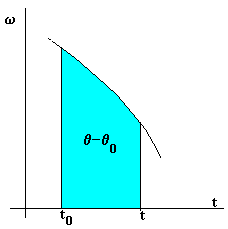
En la figura, se muestra una gráfica de la velocidad angular en función del tiempo, el área en color azul mide el desplazamiento angular total del móvil entre los instantes t₀ y t, el arco en color azul marcado en la circunferencia.

Hallamos la posición angular q  del móvil en el instante t, sumando la posición inicial q₀ al desplazamiento, calculado mediante la medida del área bajo la curva w-t o mediante cálculo de la integral definida en la fórmula anterior.

Dada la aceleración angular, hallar el cambio de velocidad angular

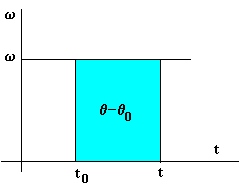
Del mismo modo que hemos calculado el desplazamiento angular del móvil entre los instantes t₀ y t, a partir de un registro de la velocidad angular w en función del tiempo t, podemos calcular el cambio de velocidad w -w₀ que experimenta el móvil entre dichos instantes, a partir de una gráfica de la aceleración angular en función del tiempo.

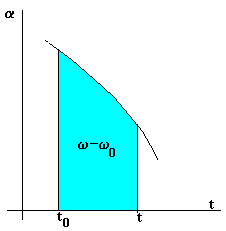En la figura, el cambio de velocidad w -w0 es el área bajo la curva a - t, o el valor numérico de la integral definida en la fórmula anterior. Conociendo el cambio de velocidad angular w -w0, y el valor inicial w0 en el instante inicial t0, podemos calcular la velocidad angular w en el instante t.

Resumiendo, las fórmulas empleadas para resolver problemas de movimiento circular son similares a las del movimiento rectilíneo.

Movimiento circular uniforme

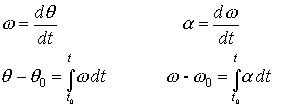
Un movimiento circular uniforme es aquél cuya velocidad angular w  es constante, por tanto, la aceleración angular es cero. La posición angular q  del móvil en el instante t lo podemos calcular integrando q -q0=w(t-t0) o gráficamente, en la representación de w en función de t.

Habitualmente, el instante inicial t₀ se toma como cero. Las ecuaciones del movimiento circular uniforme son análogas a las del movimiento rectilíneo uniforme

Movimiento circular uniformemente acelerado

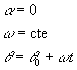
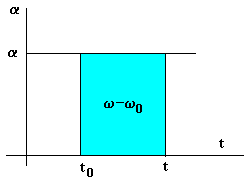	Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante. Dada la aceleración angular podemos obtener el cambio de velocidad angular w -w0 entre los instantes t0 y t, mediante integración, o gráficamente.
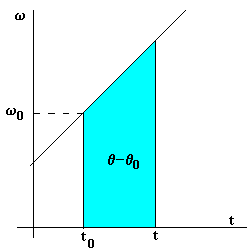	Dada la velocidad angular w en función del tiempo, obtenemos el desplazamiento q -q0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

Habitualmente, el instante inicial t₀ se toma como cero. Las fórmulas del movimiento circular uniformemente acelerado son análogas a las del movimiento rectilíneo uniformemente acelerado.

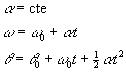
Despejando el tiempo t en la segunda ecuación  y sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ₀

Movimiento curvilíneo

Supongamos que el movimiento curvilíneo tiene lugar en el plano XY, situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es decir, el conjunto de puntos por los que pasa el móvil.

Las magnitudes que describen un movimiento curvilíneo son:

Vector posición r en un instante t.

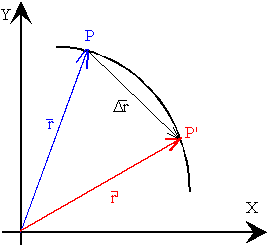Como la posición del móvil cambia con el tiempo. En el instante t el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el vector r'. Diremos que el móvil se ha desplazado Dr=r’-r en el intervalo de tiempo Dt=t'-t. Dicho vector tiene la dirección de la secante que une los puntos P y P'.

Vector velocidad

El vector velocidad media, se define como el cociente entre el vector desplazamiento Dr entre el tiempo que ha empleado en desplazarse Dt. El vector velocidad media tiene la misma dirección que el vector desplazamiento, la secante que une los puntos P y P' de la figura.

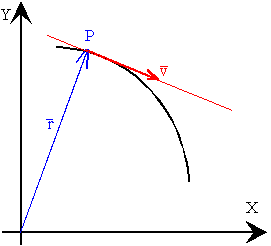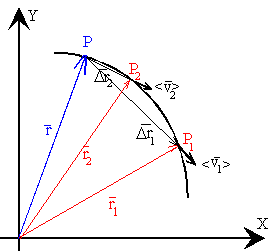
El vector velocidad en un instante, es el límite del vector velocidad media cuando el intervalo de tiempo tiende a cero. Como podemos ver en la figura, a medida que hacemos tender el intervalo de tiempo a cero, la dirección del vector velocidad media, la recta secante que une sucesivamente los puntos P, con los puntos P1, P2....., tiende hacia la tangente a la trayectoria en el punto P. En el instante t, el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.

Vector aceleración

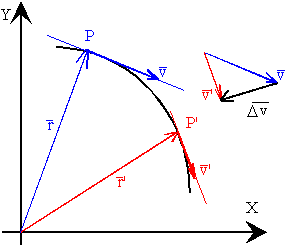En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto. En el instante t' el móvil se encuentra en el punto P' y tiene una velocidad v'. El móvil ha cambiado, en general, su velocidad tanto en módulo como en dirección, en la cantidad dada por el vector diferencia Dv=v’-v.

Se define la aceleración media como el cociente entre el vector cambio de velocidad y el intervalo de tiempo Dt=t'-t, en el que tiene lugar dicho cambio.

Y la aceleración a en un instante

Resumiendo, las ecuaciones del movimiento curvilíneo en el plano XY son

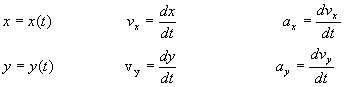
La primera fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo largo del eje X, la segunda fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo largo del eje Y, y lo mismo podemos decir respecto del eje Z.

Por tanto, podemos considerar un movimiento curvilíneo como la composición de movimientos rectilíneos a lo largo de los ejes coordenados.

Componentes tangencial y normal de la aceleración

Las componentes rectangulares de la aceleración no tienen significado físico, pero si lo tienen las componentes de la aceleración en un nuevo sistema de referencia formado por la tangente a la trayectoria y la normal a la misma.

Hallar las componentes tangencial y normal de la aceleración en un determinado instante es un problema de geometría, tal como se ve en la figura.

• Se dibujan los ejes horizontal X y vertical Y.

• Se calculan las componentes rectangulares de la velocidad y de la aceleración en dicho instante. Se representan los vectores velocidad y aceleración en dicho sistema de referencia.

• Se dibujan los nuevos ejes, la dirección tangencial es la misma que la dirección de la velocidad, la dirección normal es perpendicular a la dirección tangencial.

• Con la regla y el cartabón se proyecta el vector aceleración sobre la dirección tangencial y sobre la dirección normal.

• Se determina el ángulo q entre el vector velocidad y el vector aceleración, y se calcula el valor numérico de dichas componentes: a_t=a cosq  y  a_n=a senq

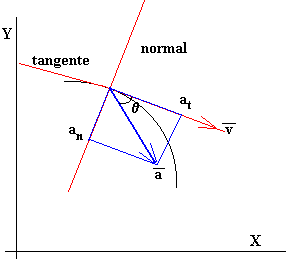
Ejemplo:

El vector velocidad del movimiento de una partícula viene dado por v=(3t-2)i+(6t²-5)j m/s. Calcular las componentes tangencial y normal de la aceleración en el instante t=2 s. Dibujar el vector velocidad, el vector aceleración y las componentes tangencial y normal en dicho instante.

1. Dadas las componentes de la velocidad obtenemos las componentes de la aceleración

v_x =3t-2 m/s,   a_x=3 m/s²
v_y=6t²-5 m/s,  a_y=12t m/s²

2. Los valores de dichas componentes en el instante t=2 s son

v_x =4 m/s,   a_x=3 m/s²
v_y=19 m/s,  a_y=24 m/s²

3. Dibujamos el vector velocidad y el vector aceleración

4. Calculamos el ángulo q  que forman el vector velocidad y el vector aceleración

• Por el producto escalar: v·a=v·a·cosq
• Calculando el ángulo que forma cada vector con el eje X, y restando ambos ángulos

5. Se calculan las componentes tangencial y normal de la aceleración

a_t=a·cosq =24.1 m/s²
a_n=a·senq=2.0 m/s²

Podemos hallar la aceleración tangencial en cualquier instante, a partir del producto escalar del vector aceleración a y el vector velocidad v.

v·a=va·cosθ=v·a_t

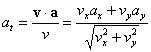
La aceleración normal, se obtiene a partir del módulo de la aceleración a y de la aceleración tangencial a_t

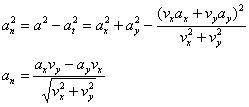
Otra forma de obtener las componentes tangencial y normal de la aceleración, es la de escribir el vector velocidad v como producto de su módulo v por un vector unitario que tenga su misma dirección y sentido u_t=v/v. La derivada de un producto se compone de la suma de dos términos

El primero, tiene la dirección de la velocidad, es la componente tangencial de la aceleración

El segundo, se puede demostrar que tiene la dirección perpendicular a la tangencial, es la componente normal de la aceleración.

siendo ρ el radio de curvatura de la trayectoria. Relación que demostraremos para el movimiento circular uniforme.

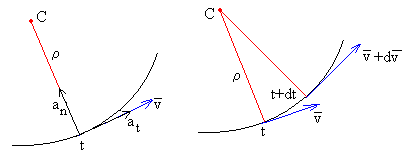
En la figura, se muestra el radio de curvatura y el centro de curvatura de una trayectoria cualesquiera en el instante t. Se dibuja la dirección del vector velocidad v en el instante t, la dirección del vector velocidad v+dv en el instante t+dt. Se trazan rectas perpendiculares a ambas direcciones, que se encuentran en el punto C denominado centro de curvatura. La distancia ente entre la posición del móvil en el instante t, y el centro de curvatura C es el radio de curvatura ρ.

Como la velocidad es un vector, y un vector tiene módulo y dirección. Existirá aceleración siempre que cambie con el tiempo bien el módulo de la velocidad, la dirección de la velocidad o ambas cosas a la vez.

• Si solamente cambia el módulo de la velocidad con el tiempo, como en un movimiento rectilíneo, tenemos únicamente aceleración tangencial.
• Si solamente cambia la dirección de la velocidad con el tiempo, pero su módulo permanece constante como en un movimiento circular uniforme, tenemos únicamente aceleración normal.
• Si cambia el módulo y la dirección de la velocidad con el tiempo, como en un tiro parabólico, tendremos aceleración tangencial y aceleración normal..

Movimiento relativo de traslación uniforme

Ejemplo 1

Un río fluye hacia el este con velocidad de c=3 m/s. Un bote se dirige hacia el este (aguas abajo) con velocidad relativa al agua de v=4 m/s.

• Calcular la velocidad del bote respecto de tierra cuando el bote se dirige hacia el este (río abajo) y cuando se dirige hacia el oeste (río arriba).
• Calcular el tiempo que tarda el bote en desplazarse d=100 m hasta el punto P y regresar de nuevo al punto de partida O.

Cuando el bote navega aguas abajo la velocidad del bote respecto de tierra es c+v, es decir de 7 m/s.   Cuando el bote navega en sentido contrario a la corriente la velocidad del bote respecto de tierra es c-v, es decir de -1 m/s.

• El tiempo que tarda el barquero en hacer el viaje de ida es t₁=d/(v+c)
• El tiempo que tarda en hacer el viaje de vuelta es t₂=d/(v-c)

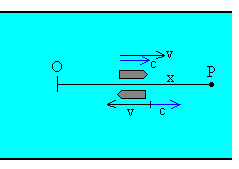El tiempo total es

Con los datos del problema t=800/7=114.3 s.

Ejemplo 2

Ahora, vamos a hacer que el bote atraviese el río y vuelva al punto de partida.

Un río fluye hacia el este con velocidad de c=3 m/s. El bote se mueve en agua quieta con una velocidad de v=4 m/s.

• ¿Cómo debe ser dirigido el bote para que llegue a un punto P situado en la orilla opuesta enfrente de O?

• Calcular la velocidad V del bote respecto de tierra.
• Calcular el tiempo que tarda el bote en desplazarse d=100 m hasta el punto P y regresar de nuevo al punto de partida O.

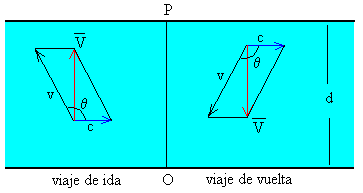
El vector velocidad V del barco respecto de tierra debe de apuntar hacia el norte.

El resultado de la suma V=v+c es 

Vj=(v·cosθ i+v·senθ j)+ci

o bien,

0=c+v·cosθ
V=v·senθ

• El ángulo θ se calcula a partir de la primera ecuación cosθ=-c/v.

• La velocidad del barco respecto de tierra V se calcula a partir de la segunda ecuación, o bien, como el cateto V del triángulo rectángulo formado por la hipotenusa v y el otro cateto c.

• El viaje de vuelta es similar al viaje de ida. El tiempo total de viaje será

Con los datos del problema,

• La velocidad del bote respecto de tierra es de .

• El ángulo que forma la proa del bote con la dirección este-oeste es θ=138.6º.

• El tiempo total de viaje será t=2·37.6=75.6 s

Ejemplo 3

Un río fluye hacia el este con velocidad de c=3 m/s. Un bote se dirige hacia el norte θ=90º con velocidad relativa al agua de v=4 m/s.

• Calcular la velocidad del bote respecto de tierra
• Si el río tiene una anchura de d=100 m, calcular el tiempo necesario para cruzarlo.
• ¿Cuál es la desviación hacia el este del bote cuando llega a la otra orilla del río?
• ¿Cómo debe dirigirse el barco para que una vez en el punto P en la orilla opuesta regrese al punto O de partida?
• Calcular el tiempo que tarda en volver al punto de partida

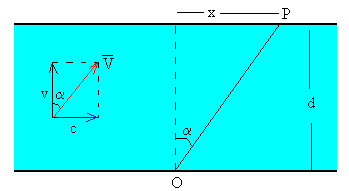
La velocidad del bote respecto de tierra V es la suma vectorial de la velocidad del bote respecto del agua v (cuando el agua está quieta) y la velocidad de la corriente de agua respecto de tierra c.

El resultado de la suma V=v+c es

Vsenα i+ Vcosα j=ci+vj

El módulo del vector resultante V es

y forma un ángulo α con la dirección norte-sur

• El tiempo que tarda en el viaje de ida es t₁=d/v,

• La desviación hacia el este es x=c·t₁=c·d/v. O bien, en el triángulo rectángulo de la figura tenemos que x=d·tanα=d·c/v.

Con los datos del problema

• La velocidad del barco respecto de tierra es V=5 m/s y su orientación respecto de la dirección norte-sur es α=36.9º.

• El tiempo que tarda en cruzar el río es t=25 s.

• El desplazamiento hacia el este del barco al llegar a la otra orilla es x=75 m.

La siguiente pregunta ya no es tan fácil. ¿Con qué ángulo debe orientarse la proa del barco para que una vez en el punto P en la orilla opuesta regrese el punto O de partida?.

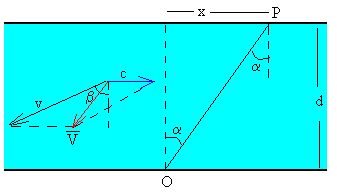
Como puede verse en la figura tenemos que calcular el ángulo β de la dirección de la velocidad v del barco respecto de la corriente para que la velocidad del barco respecto de tierra V forme un ángulo α (calculado anteriormente) con la dirección norte-sur.

El resultado de la suma V=v+c es

-V·senα i+ -V·cosα j=-v·senβ i-v·cosβ j +c i

o bien,

V·senα=v·senβ-c
V·cosα= v·cosβ

con tanα=c/v

No resulta difícil demostrar que β=2α. Para ello, se han de emplear las relaciones trigonométricas conocidas

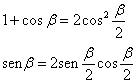
El tiempo que tarda el barco en regresar al punto de partida O es

Para demostrarlo, se ha empleado la relación trigonométrica 1+tan²α=1/cos²α

El tiempo total de viaje

Con los datos del problema tenemos

• El ángulo que forma la proa del barco con la dirección este-oeste es θ=90+β=90+2α=163.8º

• El tiempo de viaje de de vuelta t₂=89.3 s y el total t=25+89.3=114.3 s

Comparación de los tres ejemplos

El tiempo del viaje de ida (t₁=25 s) en el tercer ejemplo es el mínimo para cruzar el río, es menor que en el segundo ejemplo (t₁=37.6 s). Pero el viaje de vuelta en el tercer ejemplo (t₂=89.3 s) es de mayor duración que en el segundo ejemplo (t₂=37.6 s). Por lo que el tiempo de viaje de ida y vuelta en el segundo ejemplo (t=75.6 s) es menor que en el tercer ejemplo (t=114.3 s)  y es el mínimo que se emplea en cruzar el río.

El tiempo de viaje del primer ejemplo (t=114.3 s) es igual al tiempo de viaje en el tercer ejemplo.

Actividades

Se introduce

• La velocidad del barco en agua quieta v, en el control de edición titulado V. barco
• La velocidad de la corriente c, en el control de edición titulado V. corriente
• La dirección de la proa del barco o el ángulo θ que hace con la dirección este-oeste, actuando sobre la barra de desplazamiento, o introduciendo el valor numérico en el control de edición titulado ángulo.

Se pulsa el botón titulado Inicio, y a continuación el botón titulado Empieza.

Cuando el barco llega a la orilla opuesta, se introduce el valor del ángulo θ y se pulsa el botón titulado Empieza.

Para situar el barco en el origen, se pulsa el botón titulado Inicio.

El barco se detiene cuando se aleja del origen en la dirección de la corriente más de 100 m. Para situarlo en la posición de partida, basta actuar sobre la barra de desplazamiento que cambia el ángulo θ.

Se introduce

• Velocidad del barco en agua quieta v=4 m/s

• Velocidad de la corriente c=3 m/s

Se pulsa el botón titulado Inicio

Ejemplo 1

1. Se selecciona ángulo θ=0º en la barra de desplazamiento
   • Se pulsa el botón titulado Empieza
   • Se mide el tiempo t₁ que el barco tarda en recorrer 100 m río abajo

Cuando el barco se detiene

2. Se selecciona ángulo θ=180º en la barra de desplazamiento
   • Se pulsa el botón titulado Empieza.
   • Se mide el tiempo t₂ que el barco tarda en recorrer 100 m río arriba

Se suma los dos tiempos t= t₁+ t₂

Ejemplo 2

Se pulsa el botón titulado Inicio para situar el barco en el origen

1. Se introduce el dato relativo al ángulo θ=138.6º, se pulsa la tecla Enter o Retorno

• Se pulsa el botón titulado Empieza
• Se mide el tiempo t₁ que el barco tarda en recorrer 100 m hacia el norte hasta que llegue a la orilla opuesta.

Cuando el barco se detiene

2. Se introduce el dato relativo al ángulo θ=138.6º, pulsar la tecla Enter o Retorno

• Se pulsa el botón titulado Empieza.
• Se mide el tiempo t₂ que el barco tarda en recorrer 100 m hacia el sur hasta que regrese al origen

Se suma los dos tiempos t= t₁+ t₂

Ejemplo 3

Se pulsa el botón titulado Inicio para situar el barco en el origen

3. Se selecciona el ángulo θ=90º en la barra de desplazamiento

• Se pulsa el botón titulado Empieza
• Se mide el tiempo t₁ que el barco tarda en recorrer 100 m hasta que llegue a la orilla opuesta.

Cuando el barco se detiene

4. Se introduce el dato relativo al ángulo θ=163.8º, pulsar la tecla Enter o Retorno

• se pulsa el botón titulado Empieza.
• Se mide el tiempo t₂ que el barco tarda en recorrer 100 m hacia que regrese al origen.

Se suma los dos tiempos t= t₁+ t₂

El rozamiento por deslizamiento

El rozamiento entre dos superficies en contacto ha sido aprovechado por nuestros antepasados más remotos para hacer fuego frotando maderas. En nuestra época, el rozamiento tiene una gran importancia económica, se estima que si se le prestase mayor atención se podría ahorrar muchísima energía y recursos económicos.

Históricamente, el estudio del rozamiento comienza con Leonardo da Vinci que dedujo las leyes que gobiernan el movimiento de un bloque rectangular que desliza sobre una superficie plana. Sin embargo, este estudio pasó desapercibido.

En el siglo XVII Guillaume Amontons, físico francés, redescubrió las leyes del rozamiento estudiando el deslizamiento seco de dos superficies planas. Las conclusiones de Amontons son esencialmente las que estudiamos en los libros de Física General:

• La fuerza de rozamiento se opone al movimiento de un bloque que desliza sobre un plano.
• La fuerza de rozamiento es proporcional a la fuerza normal que ejerce el plano sobre el bloque.
• La fuerza de rozamiento no depende del área aparente de contacto.

El científico francés Coulomb añadió una propiedad más

• Una vez empezado el movimiento, la fuerza de rozamiento es independiente de la velocidad.

Explicación del origen del rozamiento por contacto

La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.

Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se presente. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.

Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que haya en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente de rozamiento dinámico es menor que el coeficiente de rozamiento estático.

Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.

La explicación de que la fuerza de rozamiento es independiente del área de la superficie aparente de contacto es la siguiente:

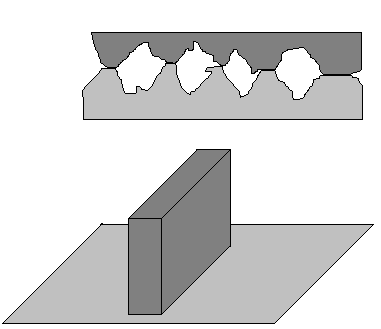
En la figura, la superficie más pequeña de un bloque está situada sobre un plano. En el dibujo situado arriba, vemos un esquema de lo que se vería al microscopio: grandes deformaciones de los picos de las dos superficies que están en contacto. Por cada unidad de superficie del bloque, el área de contacto real es relativamente grande (aunque esta es una pequeña fracción de la superficie aparente de contacto, es decir, el área de la base del bloque).

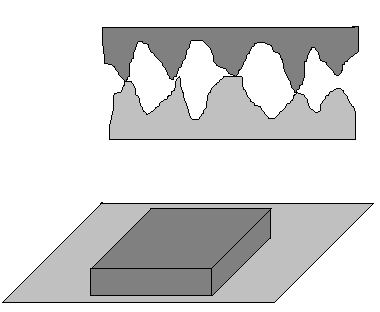
En la figura, la superficie más grande del bloque está situada sobre el plano. El dibujo muestra ahora que las deformaciones de los picos en contacto son ahora más pequeñas por que la presión es más pequeña. Por tanto, un área relativamente más pequeña está en contacto real por unidad de superficie del bloque. Como el área aparente en contacto del bloque es mayor, se deduce que el área real total de contacto es esencialmente la misma en ambos casos.

Ahora bien, las investigaciones actuales que estudian el rozamiento a escala atómica demuestran que la explicación dada anteriormente es muy general y que la naturaleza de la fuerza de rozamiento es muy compleja (Véase el artículo titulado "Rozamiento a escala atómica" en la bibliografía de este capítulo.

La fuerza normal

La fuerza normal, reacción del plano o fuerza que ejerce el plano sobre el bloque depende del peso del bloque, la inclinación del plano y de otras fuerzas que se ejerzan sobre el bloque.

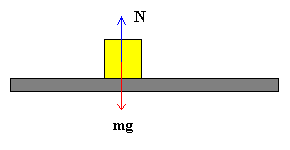Supongamos que un bloque de masa m está en reposo sobre una superficie horizontal, las únicas fuerzas que actúan sobre él son el peso mg y la fuerza y la fuerza normal N. De las condiciones de equilibrio se obtiene que la fuerza normal N es igual al peso mg N=mg

Si ahora, el plano está inclinado un ángulo q , el bloque está en equilibrio en sentido perpendicular al plano inclinado por lo que la fuerza normal N es igual a la componente del peso perpendicular al plano, N=mg·cosq

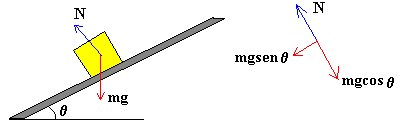
Consideremos de nuevo el bloque sobre la superficie horizontal. Si además atamos una cuerda al bloque que forme un ángulo q con la horizontal, la fuerza normal deja de ser igual al peso. La condición de equilibrio en la dirección perpendicular al plano establece  N+ F·senq =mg

Fuerza de rozamiento dinámico

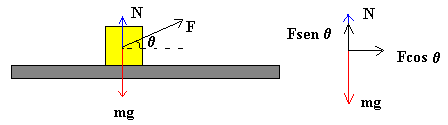
En la figura, se muestra un bloque arrastrado por una fuerza F horizontal. Sobre el bloque actúan el peso mg, la fuerza normal N que es igual al peso, y la fuerza de rozamiento F_k entre el bloque y el plano sobre el cual desliza. Si el bloque desliza con velocidad constante la fuerza aplicada F será igual a la fuerza de rozamiento F_k.

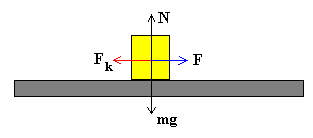
Podemos investigar la dependencia de F_k con la fuerza normal N. Veremos que si duplicamos la masa m del bloque que desliza colocando encima de éste otro igual, la fuerza normal N se duplica, la fuerza F con la que tiramos del bloque se duplica y por tanto, F_k se duplica.

La fuerza de rozamiento dinámico F_k es proporcional a la fuerza normal N.

La constante de proporcionalidad m_k es un número sin dimensiones que se denomina coeficiente de rozamiento dinámico.

El valor de m_k es casi independiente del valor de la velocidad para velocidades relativas pequeñas entre las superficies, y decrece lentamente cuando el valor de la velocidad aumenta.

Fuerza de rozamiento estático

También existe una fuerza de rozamiento entre dos objetos que no están en movimiento relativo.

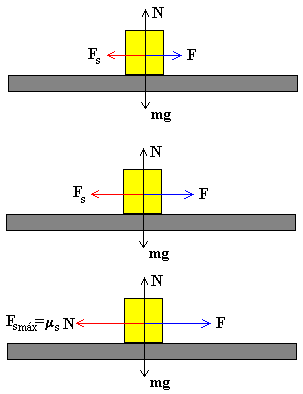
Como vemos en la figura la fuerza F aplicada sobre el bloque aumenta gradualmente, pero el bloque permanece en reposo. Como la aceleración es cero la fuerza aplicada es igual y opuesta a la fuerza de rozamiento estático F_e.

La máxima fuerza de rozamiento corresponde al instante en el que el bloque está a punto de deslizar.

La constante de proporcionalidad m_e se denomina coeficiente de rozamiento estático.

Los coeficientes de rozamiento estático y dinámico dependen de las condiciones de preparación y de la naturaleza de las dos superficies y son casi independientes del área de la superficie de contacto.

Comportamiento de un cuerpo que descansa sobre un plano horizontal

Dibujemos una gráfica en la que en el eje horizontal representamos la fuerza F aplicada sobre el bloque y en el eje vertical la fuerza de rozamiento.

1. Desde el origen hasta el punto A la fuerza F aplicada sobre el bloque no es suficientemente grande como para moverlo. Estamos en una situación de equilibrio estático

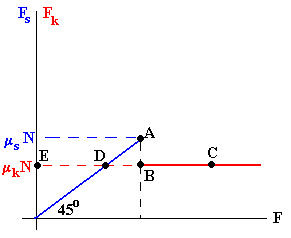
F= F_e<m_eN

En el punto A, la fuerza de rozamiento F_e alcanza su máximo valor m_eN

F= F_{e máx}=m_eN

2. Si la fuerza F aplicada se incrementa un poquito más, el bloque comienza a moverse. La fuerza de rozamiento disminuye rápidamente a un valor menor e igual a la fuerza de rozamiento dinámico, F_k=m_k N

Si la fuerza F no cambia, punto B, y permanece igual a F_{e máx} el bloque comienza moviéndose con una aceleración

a=(F-F_k)/m

Si incrementamos la fuerza F, punto C, la fuerza neta sobre el bloque F-F_k se incrementa y también se incrementa la aceleración.

En el punto D, la fuerza F aplicada es igual a F_k por lo que la fuerza neta sobre el bloque será cero. El bloque se mueve con velocidad constante.

En el punto E, se anula la fuerza aplicada F, la fuerza que actúa sobre el bloque es - F_k, la aceleración es negativa y la velocidad decrece hasta que el bloque se para.

Tablas de valores de los coeficientes

• Coeficientes de rozamiento dinámico para diferentes materiales

Fuente: Koshkin, Shirkévich. Manual de Física Elemental. Editorial Mir 1975.

• Coeficientes de rozamiento estático y dinámico

Fuente: Serway. Física. Editorial McGraw-Hill. (1992)

Dinámica de un sistema de partículas

Momento lineal e impulso

El momento lineal de una partícula de masa m que se mueve con una velocidad v se define como el producto de la masa por la velocidad

p=mv

Se define el vector fuerza, como la derivada del momento lineal respecto del tiempo

La segunda ley de Newton es un caso particular de la definición de fuerza, cuando la masa de la partícula es constante.

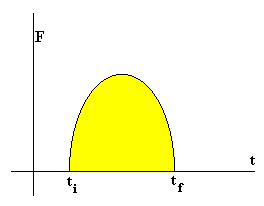Despejando dp en la definición de fuerza e integrando A la izquierda tenemos la variación de momento lineal, y a la derecha la integral que se denomina impulso de la fuerza F en el intervalo que va de ti a tf. La integral es el área sombreada bajo la curva fuerza tiempo.

En muchas situaciones físicas se emplea la aproximación del impulso. En esta aproximación, se supone que una de las fuerzas que actúan sobre la partícula es muy grande pero de muy corta duración. Esta aproximación es de gran utilidad cuando se estudian los choques, por ejemplo, de una pelota con una raqueta o una pala. El tiempo de colisión es muy pequeño, del orden de centésimas o milésimas de segundo, y la fuerza promedio que ejerce la pala o la raqueta es de varios cientos o miles de newtons. Esta fuerza es mucho mayor que la gravedad, por lo que se puede utilizar la aproximación del impulso. Cuando se utiliza esta aproximación es importante recordar que los momentos lineales inicial y final se refieren al instante antes y después de la colisión, respectivamente.

Dinámica de un sistema de partículas

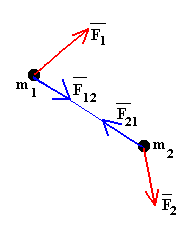
Sea un sistema de partículas. Sobre cada partícula actúan las fuerzas exteriores al sistema y las fuerzas de interacción mutua entre las partículas del sistema. Supongamos un sistema formado por dos partículas. Sobre la partícula 1 actúa la fuerza exterior F₁ y la fuerza que ejerce la partícula 2, F₁₂. Sobre la partícula 2 actúa la fuerza exterior F₂ y la fuerza que ejerce la partícula 1, F₂₁.

Por ejemplo, si el sistema de partículas fuese el formado por la Tierra y la Luna: las fuerzas exteriores serían las que ejerce el Sol (y el resto de los planetas) sobre la Tierra y sobre la Luna. Las fuerzas interiores serían la atracción mutua entre estos dos cuerpos celestes.

Para cada unas de las partículas se cumple que la variación del momento lineal con el tiempo es igual la resultante de las fuerzas que actúan sobre la partícula considerada, es decir, el movimiento de cada partícula viene determinado por las fuerzas interiores y exteriores que actúan sobre la partícula.

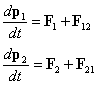
Sumando miembro a miembro y teniendo en cuanta la tercera Ley de Newton, F12=-F21, tenemos que

Donde P es el momento lineal total del sistema y F_ext es la resultante de las fuerzas exteriores que actúan sobre el sistema de partículas. El movimiento del sistema de partículas viene determinado solamente por las fuerzas exteriores.

Conservación del momento lineal de un sistema de partículas

Considérese dos partículas que pueden interactuar entre sí pero que están aisladas de los alrededores. Las partículas se mueven bajo su interacción mutua pero no hay fuerzas exteriores al sistema presentes.

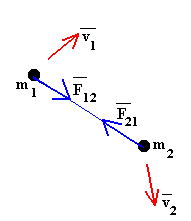La partícula 1 se mueve bajo la acción de la fuerza F12 que ejerce la partícula 2. La partícula 2 se mueve bajo la acción de la fuerza F21 que ejerce la partícula 1. La tercera ley de Newton o Principio de Acción y Reacción establece que ambas fuerzas tendrán que ser iguales y de signo contrario. F12 +F21 =0

Aplicando la segunda ley de Newton a cada una de las partículas

El principio de conservación del momento lineal afirma que el momento lineal total del sistema de partículas permanece constante, si el sistema es aislado, es decir, si no actúan fuerzas exteriores sobre las partículas del sistema. El principio de conservación del momento lineal es independiente de la naturaleza de las fuerzas de interacción entre las partículas del sistema aislado

m₁u₁+m₂u₂=m₁v₁+m₂v₂

Donde u₁ y u₂ son las velocidades iniciales de las partículas 1 y 2 y v₁ y v₂ las velocidades finales de dichas partículas.

Colisiones

Se emplea el término de colisión para representar la situación en la que dos o más partículas interaccionan durante un tiempo muy corto. Se supone que las fuerzas impulsivas debidas a la colisión son mucho más grandes que cualquier otra fuerza externa presente.

El momento lineal total se conserva en las colisiones. Sin embargo, la energía cinética no se conserva debido a que parte de la energía cinética se transforma en energía térmica y en energía potencial elástica interna cuando los cuerpos se deforman durante la colisión.

Se define colisión inelástica como la colisión en la cual no se conserva la energía cinética. Cuando dos objetos que chocan se quedan juntos después del choque se dice que la colisión es perfectamente inelástica. Por ejemplo, un meteorito que choca con la Tierra.

En una colisión elástica la energía cinética se conserva. Por ejemplo, las colisiones entre bolas de billar son aproximadamente elásticas. A nivel atómico las colisiones pueden ser perfectamente elásticas.

La magnitud Q es la diferencia entre las energías cinéticas después y antes de la colisión. Q toma el valor de cero en las colisiones perfectamente elásticas, pero puede ser menor que cero si en el choque se pierde energía cinética como resultado de la deformación, o puede ser mayor que cero, si la energía cinética de las partículas después de la colisión es mayor que la inicial, por ejemplo, en la explosión de una granada o en la desintegración radiactiva, parte de la energía química o energía nuclear se convierte en energía cinética de los productos.

Coeficiente de restitución

Se ha encontrado experimentalmente que en una colisión frontal de dos esferas sólidas como las que experimentan las bolas de billar las velocidades después del choque están relacionadas con las velocidades antes del choque, por la expresión

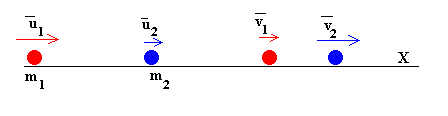
donde e es el coeficiente de restitución y tiene un valor entre 0 y 1. Esta relación fue propuesta por Newton y tiene validez solamente aproximada. El valor de uno es para un choque perfectamente elástico y el valor de cero para un choque perfectamente inelástico.

El coeficiente de restitución es la velocidad relativa de alejamiento, dividido entre la velocidad relativa de acercamiento de las partículas.

El centro de masa.

El Sistema de Referencia del Centro de Masa (sistema-C) es especialmente útil para describir las colisiones comparado con el Sistema de Referencia del Laboratorio (sistema-L).

Movimiento del Centro de Masas

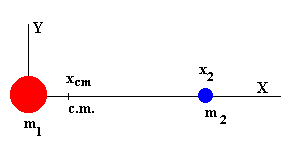
En la figura, tenemos dos partículas de masas m₁ y m₂, como m₁ es mayor que m₂, la posición del centro de masas del sistema de dos partículas estará cerca de la masa mayor.

En general, la posición r_cm del centro de masa de un sistema de N partículas es

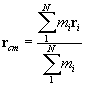
La velocidad del centro de masas v_cm  se obtiene derivando con respecto del tiempo

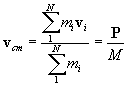
En el numerador figura el momento lineal total y en el denominador la masa total del sistema de partículas.

De la dinámica de un sistema de partículas tenemos que

El centro de masas de un sistema de partículas se mueve como si fuera una partícula de masa igual a la masa total del sistema bajo la acción de la fuerza externa aplicada al sistema.

En un sistema aislado F_ext=0 el centro de masas se mueve con velocidad constante v_cm=cte.

El Sistema de Referencia del Centro de Masas

Para un sistema de dos partículas

La velocidad de la partícula 1 respecto del centro de masas es

La velocidad de la partícula 2 respecto del centro de masas es

En el sistema-C, las dos partículas se mueven en direcciones opuestas.

Momento lineal

Podemos comprobar fácilmente que el momento lineal de la partícula 1 respecto al sistema-C es igual y opuesto al momento lineal de la partícula 2 respecto del sistema-C

p_1cm=m₁v_1cm
p_2cm=m₂v_2cm
p_1cm=-p_2cm

Energía cinética

La relación entre las energías cinéticas medidas en el sistema-L y en el sistema-C es fácil de obtener

El primer término, es la energía cinética relativa al centro de masas. El segundo término, es la energía cinética de una partícula cuya masa sea igual a la del sistema moviéndose con la velocidad del centro de masa. A este último término, se le denomina energía cinética de traslación del sistema.

En un sistema de partículas podemos separar el movimiento del sistema en dos partes:

• el movimiento de traslación con la velocidad del centro de masa
• el movimiento interno relativo al centro de masas.

Para ilustrar la importancia de centro de masas de un sistema de partículas propondremos al lector el estudio de dos programas interactivos en las próximas páginas.

Energía de un sistema de partículas

Supongamos que la partícula de masa m₁ se desplaza dr₁, y que la partícula de masa m₂ se desplaza dr₂, como consecuencia de las fuerzas que actúan sobre cada una de las partículas.

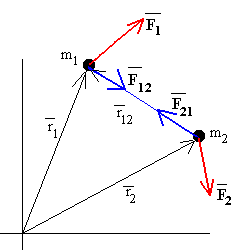El trabajo realizado por la resultante de las  fuerzas que actúan sobre la primera partícula es igual al producto escalar (F1+F12)·dr1 Del mismo modo, el trabajo realizado por la resultante de las fuerzas que actúan sobre la partícula de masa m2 será (F2+F21)·dr2

Teniendo en cuenta que el trabajo de la resultante de las fuerzas que actúan sobre una partícula modifica la energía cinética de la partícula, es decir, la diferencia entre la energía cinética final y la inicial.

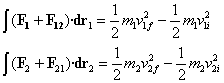
Sumando miembro a miembro, podemos escribir el trabajo como suma del trabajo de las fuerzas exteriores más el trabajo de las fuerza interiores o de interacción mutua. Se tiene en cuenta que las fuerzas interiores F₁₂=-F₂₁ son iguales y de sentido contrario

Las fuerzas interiores F₁₂ y F₂₁ realizan trabajo siempre que haya un desplazamiento relativo de la partícula 1 respecto de la 2, ya que dr₁-dr₂=d(r₁-r₂)=dr₁₂

Normalmente, la fuerza F₁₂ es conservativa (es de tipo gravitatorio, eléctrico, muelle elástico, etc.) El trabajo de una fuerza conservativa es igual a la diferencia entre la energía potencial inicial y final.

Denominando trabajo de las fuerzas exteriores a la suma

Tendremos

Entre paréntesis tenemos una cantidad que es la suma de la energía cinética de las dos partículas que forman el sistema y de la energía potencial que describe la interacción entre las dos partículas. A esta cantidad la denominamos energía U del sistema de partículas.

W_ext=U_f-U_i

El trabajo de las fuerzas exteriores es igual a la diferencia entre la energía del sistema de partículas en el estado final y la energía del sistema de partículas en el estado inicial.

Para un sistema de dos partículas, hay una sola interacción de la partícula 1 con la 2 descrita por la fuerza interna  conservativa F₁₂ o por la energía potencial E_p12. La energía del sistema U se escribe

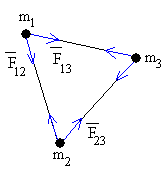Para un sistema formado por tres partículas hay tres interacciones, de la partícula 1 con la 2, la 1 con la 3 y la 2 con la 3, descritas por las fuerzas internas conservativas F12, F23, F13 o por sus correspondientes energías potenciales. La energía del sistema es

Sistema aislado

Para un sistema aislado, F_ext=0, el trabajo W_ext de las fuerzas exteriores es cero, la energía U del sistema de partículas se mantiene constante. Para un sistema de dos partículas cuya interacción mutua está descrita por la energía potencial E_p12.

La fuerza exterior F_ext es conservativa

El trabajo de la fuerza exterior es igual a la diferencia entre de energía potencial inicial y la final

W_ext=E_pi-E_pf

Tenemos por tanto que U_i+E_pi=U_f+E_pf=cte

Para un sistema de dos partículas bajo la acción de la fuerza conservativa peso, la conservación de la energía se escribirá

Fórmula de Stokes

Descripción

La esfera se mueve bajo la acción de las siguientes fuerzas: el peso, el empuje (se supone que el cuerpo está completamente sumergido en el seno de un fluido), y una fuerza de rozamiento que es proporcional a la velocidad de la esfera (suponemos que el flujo se mantiene laminar).

El peso es el producto de la masa por la aceleración de la gravedad g. La masa es el producto de la densidad del material ρ_e por el volumen de la esfera de radio R.

De acuerdo con el principio de Arquímedes, el empuje es igual al producto de la densidad del fluido ρ_f, por el volumen del cuerpo sumergido, y por la aceleración de la gravedad.

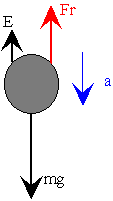La fuerza de rozamiento es proporcional a la velocidad, y su expresión se denomina ley de Stokes donde h es la viscosidad del fluido. La ecuación del movimiento será, por tanto,

La velocidad límite, se alcanza cuando la aceleración sea cero, es decir, cuando la resultante de las fuerzas que actúan sobre la esfera es cero.

Despejamos la velocidad límite v_l

Integramos la ecuación del movimiento para obtener la velocidad de la esfera en función del tiempo. Escribimos la ecuación del movimiento de la siguiente forma

donde F es la diferencia entre el peso y el empuje F=mg-E, y k=6πRh

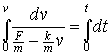
Obtenemos

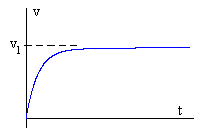Esta ecuación nos dice que se alcanza la velocidad límite vl después de un tiempo teóricamente infinito. Si representamos v en función del tiempo t la gráfica tienen una asíntota horizontal en v=vl.

Integramos la expresión de la velocidad en función del tiempo para obtener  la posición x del móvil en función del tiempo t. Suponemos que la esfera parte del origen x=0, en el instante inicial t=0.

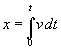
se obtiene

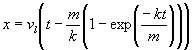
Dado que la exponencial tiende a cero rápidamente a medida que transcurre el tiempo, vemos que al cabo de un cierto tiempo, el desplazamiento x del móvil será proporcional al tiempo t.

Las diferencias entre el movimiento de un cuerpo en caída libre y cuando cae en el seno de un fluido viscoso se pueden resumir en el siguiente cuadro

Actividades

Se introducen los siguientes datos:

• La densidad (en g/cm³) y el radio (en mm) de la esfera

• La densidad (en g/cm³) y la viscosidad (en kg/m·s) del fluido

Determinar la dependencia de la velocidad límite con el radio de la esfera, con la densidad del material, con la densidad y viscosidad del fluido:

1. Elegir esferas de distinto radio, del mismo material y que se muevan en el mismo fluido.
    
2. Elegir esferas del mismo radio pero de distinto material, y que se muevan en el mismo fluido.
    
3. Cambiar el fluido en el que se mueven las esferas, manteniendo sus dimensiones y su material constitutivo.

El círculo de color rojo representa la esfera que cae en el seno de un fluido viscoso. Al lado se representa las fuerzas sobre la esfera. En color rojo la fuerza F constante resultante de restar el peso del empuje del fluido, en color azul la fuerza de rozamiento proporcional a la velocidad kv. Cuando ambas flechas son iguales, la velocidad de la esfera es constante e igual a la velocidad límite.

Ejemplo:

En la experiencia que realizamos en el laboratorio para medir la viscosidad de un aceite de automóvil empleamos perdigones de plomo. Los datos son

• Densidad del plomo ρ_e=11.35 g/cm³
• Radio de la esfera de plomo R=1.96 mm
• Densidad del aceite ρ_f=0.88 g/cm³
• Viscosidad del aceite η=0.391 kg/(m·s)

Se alcanza el 99.5% de la velocidad límite constante en el instante t tal que

Donde k=6πRη=0.014

La masa de la esfera es m=ρ_e4/3πR³=3.58·10^-4 kg

Despejamos el tiempo t=0.13 s

La esfera se habrá desplazado en este tiempo x=0.023 m

Si dejamos caer la bolita desde la superficie del aceite, podemos comenzar a tomar medidas con seguridad 3 centímetros por debajo de dicha superficie.

Como veremos más adelante el rango de validez de la fórmula de Stokes limita el valor del radio R de la esfera de un determinado material que empleamos para la medida de la viscosidad de un fluido dado.

Movimiento ondulatorio

Podemos observar ejemplos de movimiento ondulatorio en la vida diaria: el sonido producido en la laringe de los animales y de los hombres que permite la comunicación entre los individuos de la misma especie, las ondas producidas cuando se lanza una piedra a un estanque, las ondas electromagnéticas producidas por emisoras de radio y televisión, etc.

Comencemos por un fenómeno familiar, la propagación de las ondas en la superficie de un estanque. La superficie de un líquido en equilibrio es plana y horizontal. Supongamos que arrojamos un objeto a un estanque. Cuando el objeto entra en contacto con la superficie del agua se produce una perturbación de su estado físico. Una perturbación de la superficie produce un desplazamiento de todas las moléculas situadas inmediatamente debajo de la superficie. Teniendo en cuenta las fuerzas que actúan sobre los elementos de fluido: peso del fluido situado por encima del nivel de equilibrio y la tensión superficial, se llega a una ecuación diferencial, a partir de la cual se puede calcular la velocidad de propagación de las ondas en la superficie de un fluido. El análisis de esta situación es complicado, pero veremos con detalle una más simple la propagación de las ondas transversales en una cuerda.

Antes de que Hertz realizara sus experimentos para producir por primera vez ondas electromagnéticas, su existencia había sido predicha por Maxwell como resultado de un análisis cuidadoso de las ecuaciones del campo electromagnético. El gran volumen de información que se ha acumulado sobre las ondas electromagnéticas (cómo se producen, propagan, y absorben) ha posibilitado el mundo de las comunicaciones que conocemos hoy en día.

Aunque el mecanismo físico puede ser diferente para los distintos movimientos ondulatorios, todos ellos tienen una característica común, son situaciones producidas en un punto del espacio, que se propagan a través del mismo y se reciben en otro punto.

Descripción de la propagación

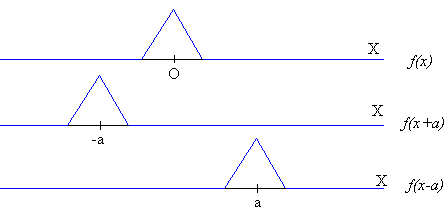
Consideremos una función Y =f(x), si reemplazamos x por x-a, obtenemos la función Y =f(x-a). La forma de la curva no cambia, los mismos valores se obtienen de Y para valores de x aumentados en a. Si a es una cantidad positiva, la curva se traslada sin cambiar de forma hacia la derecha desde el origen a la posición a. Del mismo modo Y =f(x+a) corresponde a un desplazamiento de la función hacia la izquierda, en la cantidad a.

Si a=vt, donde t es el tiempo, la función "se mueve" con velocidad v. Y =f(x-vt) describe la propagación de una perturbación representada por la función f(x), sin distorsión, a la largo del eje X, hacia la derecha, con velocidad v.

Ecuación diferencial del movimiento ondulatorio

Cada vez que conozcamos que una propiedad física Y, por ejemplo el desplazamiento de un punto de una cuerda, satisface la ecuación diferencial

podemos estar seguros que estamos describiendo un movimiento ondulatorio que se propaga a lo largo del eje X, sin distorsión y con velocidad v.

Podemos comprobar que una solución de ésta ecuación diferencial es Y =f(x-vt).

Clases de movimiento ondulatorios

• El movimiento ondulatorio transversal es aquél en el que la dirección de propagación es perpendicular a la dirección de vibración, tal como sucede en una cuerda, o las ondas electromagnéticas.

• En el movimiento ondulatorio longitudinal coinciden la dirección de vibración y de propagación, un ejemplo es el del sonido.

Actividades

En el applet  podemos observar la propagación de una perturbación en forma de un pulso triangular, sin distorsión, a lo largo del eje X, hacia la derecha. Dicha perturbación puede ser producida, por ejemplo, al dar un martillazo en el extremo de una barra de hierro.

En la parte inferior de la ventana del applet, vemos una imagen animada del movimiento de la fuente que produce el movimiento ondulatorio, situada en el origen. A la derecha, vemos el movimiento de las partículas del medio a medida que se propaga la perturbación. En particular, podemos observar el movimiento de las partículas situadas en la posición x=3.0 que tienen un color azul, diferente del resto, que son de color rojo.
Las partículas se mueven, pero retornan a sus posiciones de equilibrio cuando pasa la perturbación. En un movimiento ondulatorio no hay por tanto, transporte de materia, lo que se propaga es el estado de movimiento.

En el applet observamos el movimiento de las partículas del medio y la representación gráfica en cada instante, de su desplazamiento Y (en el eje vertical) de la posición inicial de equilibrio  (por razón de claridad se ha exagerado este desplazamiento). Esta representación, se describe matemáticamente mediante la función Y =f(x-vt), tal como se ha justificado en el primer apartado.

Se introduce

• el valor de la velocidad de propagación en el control de edición titulado Velocidad de propagación,

Se pulsa el botón titulado Empieza.

Para detener en cualquier momento el movimiento, se pulsa el botón titulado Pausa, se reanuda el movimiento pulsando el mismo botón titulado ahora Continua. Para observar el movimiento paso a paso, se pulsa varias veces el botón titulado Paso, se reanuda el movimiento pulsando el botón Continua.

Interferencia de ondas producidas por dos fuentes

Interferencia de ondas producidas por dos fuentes sincrónicas

Consideremos dos fuentes puntuales S₁ y S₂ que oscilan en fase con la misma frecuencia angular w , y que emiten ondas armónicas.

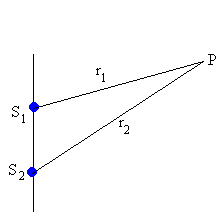Cuando emite solamente S1 el punto P describe el Movimiento Armónico Simple (M.A.S.) de amplitud A1 y frecuencia angular w . y1=A1·sen(kr1-w t) Cuando emite solamente S2 el punto P describe el M.A.S. de amplitud A2 y frecuencia angular w . y2=A2·sen(kr2-w t)

Cuando emiten simultáneamente S₁ y S₂. El punto P describe un M.A.S. que es la composición de dos M.A.S. de la misma dirección y frecuencia. Los casos más importantes son aquellos en los que los M.A.S. están en fase y en oposición de fase.

En fase o interferencia constructiva.

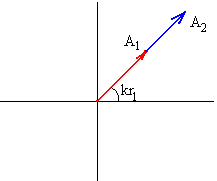Dos M.A.S están en fase cuando la diferencia de fase kr1-kr2 es un múltiplo entero de 2p .Teniendo en cuenta que k=2p /l La amplitud resultante es la suma de amplitudes A=A1+A2

En oposición de fase o interferencia destructiva.

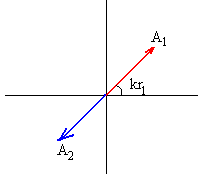Dos M.A.S están en oposición de fase cuando la diferencia de fase kr1-kr2 es un múltiplo entero de p .Teniendo en cuenta que k=2p /l La amplitud resultante es la diferencia de amplitudes. Si ambas son iguales, el punto P no se mueve.

Resumiendo, las condiciones de interferencia son

Amplitud resultante

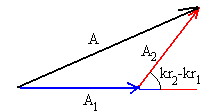
En el caso general, es necesario sumar vectorialmente las amplitudes para obtener la resultante.

Si la separación a de las fuentes S₁ y S₂ es pequeña comparada con la distancia desde las fuentes hasta la pantalla, podemos despreciar la pequeña diferencia entre r₁ y r₂ y suponer que las amplitudes A₁ y A₂ son prácticamente iguales. Podemos escribir

donde r₁- r₂=a senq .

A partir de esta expresión podemos hallar las direcciones q   para las cuales la interferencia es constructiva o destructiva

También podemos hallar las posiciones x sobre la pantalla, que registran interferencia constructiva y destructiva, para ello hacemos la aproximación siguiente: si el ángulo q  es pequeño, senq ≈tgq =x/D

Intensidad

La intensidad de un movimiento ondulatorio es proporcional al cuadrado de la amplitud, de modo que

I es la intensidad resultante en el punto P cuando las dos fuentes emiten simultáneamente, e I₀ es la intensidad en el punto P debido a una sola de las fuentes.

En la interferencia  constructiva a =np y por tanto la intensidad I=4I₀. En cambio, en la interferencia destructiva a =(2n+1)p /2 y la intensidad I=0.

Es importante señalar que en la interferencia constructiva la intensidad en P debida a las dos fuentes es 2² veces la que corresponde a una de las fuentes.

Regresar