TEORIA

PARÁMETROS PRIMARIOS EN UNA LÍNEA DE TRANSMISIÓN

CABLE COAXIAL

Las fórmulas enunciadas a continuación están basadas en el diagrama del cable coaxial que aparece a continuación en donde el dieléctrico tiene un radio interno a y uno externo b.

Alta Frecuencia

Resistencia Distribuida
Si la frecuencia es muy alta, es decir, frecuencias de decenas de centenares de MHz y aun más altas, y la profundidad de piel d. Dado que la corriente de la línea fluye a través de los dos conductores del cable la resistencia es la suma en serie de éstas dos:

Donde Rhf(coax) es la resistencia distribuida total de la línea coaxial a frecuencias muy altas. Aquí a es el radio exterior del conductor interior, b el radio interior del conductor exterior y . es la resistividad de superficie del material del conductor.

Capacitancia Distribuida

Por definición, la capacitancia entre dos conductores cualesquiera o elementos de conductores es la razón de la magnitud de cualquiera de las cargas iguales y opuestas en ellos a la diferencia de potencial asociada con las cargas. Entonces, si es la capacitancia entre los conductores de una línea coaxial para la longitud , = /(Vb – Va), y la capacitancia distribuida de la línea es C = / = (/)/ (Vb – Va). Reemplazando en la ecuación obtenemos:


	micromicrofaradios/metro

Donde ke’ es la constante del dieléctrico real del material sin pérdidas, que llena el espacio interconductor, tenemos que = 8,85 x 10 –12 faradios/metro es la permitividad del espacio libre.
También se expresa así:

La capacitancia distribuida de una línea de transmisión coaxial está generalmente en el rango de cerca de 25 a 200 micromicrofaradios/metro y valores entre 50 y 100 micromicrofaradios /metro son más comunes.

Conductancia Distribuida

En casos muy especiales, el espacio interconductor de una línea de transmisión se llena de material que conduce electricidad por medio del flujo de portadores de carga, ya sean electrones o iones. Entre esos materiales están: la tierra húmeda, las soluciones electrolíticas y los emplastes o la cerámica con carbón disperso, cuyas propiedades portadoras se describirán con la ayuda de un valor verdadero de conductividad que tiene el mismo significado que la conductividad de un metal.
Por esto encontramos que la conductancia distribuida de una línea coaxial es la siguiente:

La cantidad se utiliza para designar las pérdidas de un dieléctrico en campos eléctricos a-c, se llama factor de pérdida o tangente del ángulo de pérdida del material.
La ecuación anterior nos muestra que la conductancia distribuida de una línea de transmisión coaxial es directamente proporcional a la frecuencia, si el factor de pérdida tand y la capacitancia distribuida de la línea don independientes de la frecuencia. Además la conductancia por unidad de longitud puede determinarse fácilmente a partir de la expresión de la capacitancia anterior utilizando la analogía con la corriente, así:

donde es la conductividad del dieléctrico que existe entre los conductores a la frecuencia de operación.

Inductancia Distribuida

Este cuarto coeficiente de circuito distribuido, la inductancia distribuida, es el único de estos cuatro coeficientes para una línea de transmisión que en algunos casos tiene que ser determinado como la suma de componentes “externas” e “internas”.
La inductancia externa distribuida de la línea Lx, definida como la cantidad de flujo externo que enlaza el circuito por unidad de longitud por unidad de corriente es:

henrios/m.

La inductancia por unidad de longitud para un cable coaxial esta determinada por la ecuación:

donde es la permitividad del dieléctrico que existe entre los conductores, generalmente o. Ésta es una inductancia externa, puesto que en su determinación no se toma en cuenta ningún flujo dentro de ninguno de los conductores.

También debemos incluir la expresión para la impedancia característica de un cable coaxial con las fórmulas paramétricas:

Baja Frecuencia

Ahora se describirán las expresiones para obtener los valores de los parámetros a frecuencias muy bajas donde no existe un efecto de piel y en donde la corriente se supone que se distribuye uniformemente a lo largo de la sección transversal.
La capacitancia y la inductancia por unidad de longitud no se ven afectadas por la distribución de corriente, por lo tanto sus expresiones matemáticas son idénticas a las descritas para un cable coaxial a altas frecuencias.
La resistencia por unidad de longitud se puede calcular por métodos de cd, donde L = 1m y
es la conductividad de los conductores interno y externo. Así tenemos:

La inductancia externa por unidad de longitud a altas frecuencias constituye la mayor parte de la inductancia total, pero hay que agregarle términos menores que representan las inductancias internas de los conductores interno y externo. A bajas frecuencias, la inductancia total se obtiene combinando esas expresiones, obteniendo así:

Frecuencia Intermedia

En el caso en que la profundidad de piel no es ni muy grande ni muy pequeña en comparación con el radio la distribución de corriente esta regida por la funciones de Bessel y tanto la resistencia como la inductancia interna tienen expresiones complicadas. Existen manuales con valores tabulados que es necesario utilizar en estos casos.

LÍNEAS BIFILARES

Alta Frecuencia

Resistencia Distribuida

La resistencia por unidad de longitud es el doble de la del conductor central del cable coaxial:

Capacitancia Distribuida

Para la línea bifilar de la figura con conductores de radio a y conductivida con una separación entre centros igual a d y un medio de permeabilidad , permitividad y conductividad , la capacitancia esta dada por:

Conductancia Distribuida

La conductancia por unidad de longitud se puede escribir inmediatamente, por inspección de la expresión para la capacitancia:

Inductancia Distribuida

La inductancia puede encontrarse de LextC = . Y resulta:

Finalmente, usando las expresiones para la capacitancia y la inductancia externa se obtiene un valor para la impedancia característica:

Baja Frecuencia

A bajas frecuencias, en donde suponer una distribución de corriente uniforme, se deben modificar una vez más las expresiones de L y R. Las expresiones de C y G son las mismas mencionadas para una línea bifilar operando a altas frecuencias.
La inductancia por unidad de longitud debe aumentarse al doble de la inductancia interna de un alambre recto de sección circular:

La resistencia se transforma en el doble de la resistencia para cd de un alambre de radio a, conductividad y de una unidad de longitud:

Placas Paralelas

Resistencia Distribuida

A frecuencias que son lo suficientemente altas para que los conductores tengan un espesor de por lo menos tres profundidades de piel, el resultado es ohmios/m. Para frecuencias intermedias, la resistencia distribuida es el valor dado por la ecuación anterior multiplicado por un factor.

Capacitancia Distribuida

Si dos conductores infinitos planos paralelos llevan densidades de carga de superficie uniformes, iguales y opuestas de magnitud el campo de flujo eléctrico está limitado enteramente al espacio entre ellos y es normal a las superficies del conductor, teniendo una densidad constante de El campo eléctrico está dado por

Al obtener esto, se puede encontrar la diferencia de potencial V entre los conductores que sería

De ahí relacionando la ecuación anterior encontramos que la capacitancia distribuida del conductor plano paralelo está dada aproximadamente por:

Conductancia Distribuida

La conductancia distribuida de todas las líneas de trasmisión está dada por la ecuación expuesta en línea coaxial. Para la línea de trasmisión ideal de conductores planos paralelos, ignorando los efectos de los bordes, esto toma la forma específica de

Para que esta expresión sea aplicable, el medio interconductor cuyo factor de pérdida es debe contener todo el campo eléctrico que rodea los conductores de la línea. Esta condición se puede satisfacer para conductores planos paralelos si el medio llena el espacio entre ellos.
Inductancia Distribuida
Si los conductores actuales, en la línea de transmisión de conductores planos paralelos, tienen un ancho finito w, y si las corrientes y campos son los de planos infinitos la magnitud de corriente en cada conductor de la línea será, I=Jszw amperios. La inductancia externa distribuida de la línea, definida como el flujo total externo a los conductores, que enlaza el circuito, por unidad de corriente, se convierte en:

Microcintas

Línea de transmisión constituida por una cinta conductora y una superficie conductora paralela de anchura muy superior; estos dos conductores son solidarios de las dos caras de un soporte dieléctrico de pequeño espesor.
La líneas de microcintas son ampliamente usadas para interconectar circuitos lógicos de alta velocidad en las computadoras digitales porque estas pueden ser fabricadas por técnicas automatizadas y ello proporciona una señal uniforme en toda la trayectoria.
La impedancia de una línea de microcinta está en función del ancho de la línea de cinta, el espesor de la línea de cinta, la distancia entre la línea y área de tierra, y la constante relativa del dieléctrico del material. Para encontrar la impedancia de una microcinta se relaciona la ecuación de otra línea de trasmisión como es la del alambre sobre tierra (wire over ground), cuya impedancia es,

donde,

: constante relativa del dieléctrico del medio ambiente.
h : distancia entre el centro del alambre y el área de tierra.
d : diámetro del alambre.

La constante efectiva relativa del dieléctrico para una línea de microcinta puede relacionarse con la constante relativa del dieléctrico del material. DiGiacomo y coayudantes descubrieron una ecuación empírica para la constante efectiva relativa del dieléctrico de la línea de microcinta como medida de propagación del tiempo y la constante relativa del dieléctrico en varios materiales.

donde,
: constante relativa del dieléctrico del medio ambiente.

: constante efectiva relativa del dieléctrico de la línea de microcinta.

La sección transversal de la línea de microcinta es rectangular. Debemos transformar los parámetros circulares a su equivalente en rectangular. Springfield descubrió una ecuación empírica para la transformación,

d = 0.67 w (0.8 + t/w)

donde,
d: diámetro de la línea sobre tierra
w : ancho de la línea de microcinta
t : espesor de la línea de microcinta

Sustituyendo la ecuación para la constante del dieléctrico y para la equivalencia del diámetro en la ecuación de la impedancia característica de la línea de alambre sobre tierra, obtenemos

donde,
: constante relativa del dieléctrico del material.
h : distancia entre el centro del alambre y el área de tierra.
w : ancho de la línea de microcinta
t : espesor de la línea de microcinta

Esta ecuación es para la impedancia característica de una línea angosta de microcinta. La velocidad de propagación es,

La impedancia característica para una línea ancha de microcinta fue derivada por Assadourian y otros, está expresada por

PARÁMETROS SECUNDARIOS EN UNA LÍNEA DE TRANSMISIÓN

Entre los parámetros secundarios tenemos a A 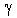se le da el nombre de constante de propagación. Es evidente que cada línea de transmisión tiene su propio valor particular para 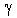a determinada frecuencia, dependiendo de su geometría y de los materiales que la compongan, pues los cuatro parámetros básicos por unidad de longitud R, L, G y C intervienen en la ecuación que la define, además de la variable w. La constante de propagación es igual a la raíz cuadrada del producto de la impedancia en serie por la admitancia en paralelo de la línea, lo cual se puede escribir de la forma siguiente: y como ésta es también un número complejo puede representarse como: en donde la parte real, , indica la atenuación que sufre la onda de voltaje, o de corriente según sea el caso, conforme viaja o se propaga a lo largo de la línea; y , que es la parte imaginaria, indica la rapidez del cambio de fase de la onda conforme se propaga. Las unidades de la constante de atenuación a son nepers por metro, y las de la constante de fase

son radianes por metro. Sin embargo, es más común especificar en decibeles por metro. Para determinar la impedancia característica se utiliza la siguiente ecuación:

Hay que mencionar que así como la constante de propagación g tiene un valor determinado para cada línea de transmisión, también la impedancia características tendrá su valor particular, dependiendo de la geometría y las dimensiones de la línea, así como de la frecuencia de operación w. Este parámetro, Zo, es comúnmente proporcionado por los fabricantes de cables en sus catálogos de productos y no es realmente necesario conocer los parámetros básicos R, L, G y C de línea.

Ecuación General de una Línea de Transmisión

Una vez determinados los parámetros básicos de una línea (L, C, R y G) se encontrar la relación que existe entre las ondas de voltaje corriente que viajan a lo largo de ella, desde el generador hacia la carga, así como la velocidad con la q lo hacen. El método de análisis considera que dichos parámetros básicos están distribuidos uniformemente a lo largo de toda la longitud de los cables que constituyen a la línea, y no concentrados como un circuito ordinario.
Tanto la línea de “ida” como en la “de regreso” tienen su propia resistencia e inductancia, pero es más común, por simplicidad representar el circuito equivalente, como se indica en la figura a continuación.

La ecuación diferencial que debe satisfacer la onda de voltaje es la siguiente:

A esta ecuación se le llama comúnmente, por razones históricas, como la ecuación del teregrafista. También se puede obtener la ecuación diferencial de segundo grado que satisface la onda de corriente:

Las soluciones de las ecuaciones anteriores se pueden determinar fácilmente si se considera que las variaciones del voltaje y la corriente con relación al tiempo son senoidales, y como las ecuaciones son lineales y de coeficientes constantes es posible utilizar fasores, sustituyendo al voltaje v(z,t) por y la corriente i(z,t) por Al efectuar dichas situaciones se obtiene:

Finalmente al derivar y sustituir en el resultado a la expresión, se obtiene la ecuación diferencial de segundo grado en forma fasorial:

cuya solución general es la fórmula:

La velocidad de fase vp, que se define como: , donde es la constante de fase o parte imaginaria de la constante de propagación, y w es la frecuencia angular. La línea tiene una longitud total física, medida en metros, y una longitud total eléctrica correspondiente, medida en longitudes de onda . Por definición es la distancia entre puntos sucesivos de la onda que tienen la misma fase eléctrica.

Si entre los conductores hay aire, se puede considerar que la velocidad de la onda es igual a la de la luz en el espacio libre, es decir 300000 km/seg; pero si el medio tiene una constante dieléctrica relativa er mayor que la unidad, entonces la onda se propaga con una velocidad menor que la de la luz. Al reducirse la velocidad de propagación, la longitud de onda automáticamente se reduce también, como si la onda fuese comprimida a lo largo del eje z. Esta nueva longitud de onda dentro del medio de propagación sin pérdidas se calcula como:

donde es la longitud de onda en el espacio libre a la misma frecuencia. Para modos de propagación TEM, como son los casos analizados anteriormente, en los que generalmente se puede considerar = 0, la velocidad de propagación v a la que viaja la potencia de la señal es igual numéricamente a la velocidad de fase vp. De manera tal que si l es la longitud total de la línea, el tiempo total que tarda un punto arbitrario con determinada fase en recorrer la distancia desde el generador hasta la carga es igual a:

Este tiempo, td, es el tiempo de retardo de la línea.

Propagación de Líneas Acopladas
La onda incidentes es la onda de voltaje que parte del generador hacia una carga situada en el otro extremo de la línea. El voltaje y la corriente de la onda pura incidente se escribe como

De estas ecuaciones se destaca que independientemente de la atenuación a de la línea, el cociente de voltaje sobre la corriente siempre es igual a Zo. Este resultado es independiente de z, o sea que es el mismo para todos los puntos de línea. Puede pensarse que si al final de una línea finita de impedancia característica Zo se conecta una carga con impedancia también Zo la línea se comportará igual a como si fuese infinita, en el sentido de que no habrá una onda reflejada. La gran importancia que tiene la impedancia característica de una línea en la práctica es que al usarse un valor igual como carga, esto hace parecer a la línea como infinita; en otras palabras una línea de longitud finita que esté terminada con una carga igual a su impedancia característica le entregará toda la potencia incidente disponible a la carga, cuando esto ocurre, se dice que la línea está acoplada.

Sin embargo, si la impedancia característica, Zo, y la impedancia de la carga, ZL, son diferentes, la línea ya no se comportará como si fuese infinita; estará desacoplada y habrá una onda reflejada.

La onda total de voltaje en una línea desacoplada estará dada por la superposición, para toda z, de la onda incidente y la onda reflejada, Vr(z)

Por lo que se refiere a la potencia promedio entregada a la carga, ésta debe ser igual a la potencia promedio de entrada, ya que se está considerando que la línea no tiene pérdidas.
Pprom-carga = Pprom-entrada = ½ Re [V(z) I*(z)]

Impedancia De Entrada De Una Línea Terminada Con Una Carga Arbitraria
Considérese una línea finita de longitud l como la de la figura mostrada. De ahora en adelante, conviene tomar al punto donde está la carga como z = 0, por lo que el generador estará situado en z = -1. Esta es una práctica común y no implica ninguna dificultad adicional. Las ecuaciones que describen el comportamiento de las ondas totales de voltaje y corriente son las mismas, pues la coordenada z crece en el mismo sentido que antes, de izquierda a derecha.

La impedancia Z vista hacia la derecha (en dirección hacia la carga) desde cualquier punto en la línea está dada, a partir de las ecuaciones de voltaje y corriente, por:

(a)

Si z = -1, la impedancia de entrada vista por el generador hacia la derecha, será entonces:

(b)

Ahora bien, en z = 0, donde está la carga ZL de la ecuación (a) se obtiene:

De donde, (c)

Al coeficiente B/A se le da el nombre de coeficiente se le da el nombre de coeficiente de reflexión en el punto de carga. Se designa por la letra ? y generalmente es una cantidad compleja.
Si el numerador y el denominador de la ec. (b) se dividen entre , se tiene:

Y como B/A = : (d)

Esta ecuación permite calcular la impedancia de entrada de la línea si se conocen su longitud, su impedancia característica, la corriente de propagación 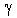y el coeficiente de reflexión en el punto donde está la carga. Otra ecuación alternativa, en función de la impedancia de carga en lugar del coeficiente de reflexión, se puede obtener usando la ec. (c) y escribiendo la ec. (b) como:

Y al dividir numerador y denominador entre 2 cosh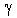l, , queda finalmente:

Impedancia De Entrada De Una Línea Terminada En Corto Circuito
Como caso particular se considerará ahora una línea en cuyo extremo final se tiene un corto circuito. Al evaluar la ecuación de solución general de voltaje en la carga, donde z = 0, y dado que el voltaje en ese punto vale cero, se obtiene:

V (0) = A + B = 0 à B = -A ( = -1)

Línea terminada en corto circuito.

Utilizando la relación anterior, las expresiones para V (z) e I (z) pueden rescribirse, a partir de las ecuaciones generales de voltaje y corriente, de la siguiente forma:

La impedancia de entrada vista por el generador puede obtenerse sustituyendo z = -1 y tomando el cociente tradicional de las dos relaciones anteriores:

(e)

Esta expresión también pudo haberse obtenido directamente de la ecuación (e), sustituyendo ZL = 0, pero a continuación se verá por qué conviene realizar el rápido cálculo anterior por separado.
En la práctica, medir la impedancia de entrada de una línea corta terminada en circuito cerrado permite medir indirectamente los parámetros R y L de la línea. Si la línea es lo suficientemente corta, de tal modo que , los exponenciales en la ec. (f) pueden expandirse para simplificar a la misma en forma muy aproximada:

(g)

Ahora bien, si las ecuaciones de Z0 y g se multiplican:

(h)

Finalmente, igualando la ec (g) con la ec. (h): (i)

Impedancia de Entrada de una Línea Terminada en Circuito Abierto

Línea terminada en circuito abierto.

El procedimiento que se realiza para analizar una línea terminada en circuito abierto es similar al procedimiento a seguir con las líneas terminadas en circuito cerrado.
Para un circuito abierto al final de la línea se tendrá una corriente igual a cero. Por lo tanto,

por lo que,

y la impedancia vista en z = -1

Si suponemos nuevamente que la línea es corta , la ecuación se puede reducir a:

Ahora dividiendo a 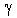entre Zo:

teniendo que:

Por lo tanto ,la impedancia de entrada medida a cierta frecuencia angular w para una línea corta de longitud l terminada en circuito abierto permite obtener los parámetros G y C de la línea.

Reactancia de Entrada y Aplicaciones de Líneas sin Pérdidas Terminadas en Corto y Circuito Abierto

Además de ser utilizada para transmitir información. como lo es en la mayor parte de los csos, una línea puede servir también como elemento de un circuito. En el rango de frecuencias de UHF (300 MHz a 3 GHz) es difícil fabricar elementos de circuitos con parámetros concentrados, pues la longitud de onda varía entre 10 cm y 1 m. En estos casos, se pueden diseñar segmentos de transmisión que produzcan una impedancia inductiva o capacitiva, y que se puedan utilizar para acoplar una carga arbitraria con la línea principal y efectuar la máxima transferencia de potencia posible. A estas altas frecuencias, las pérdidas en una línea se pueden considerar como despreciables, por lo que se refiere al cálculo de Zo, de 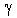y de la impedancia vista en cualquier punto de la línea, puesto que . Al hacer estas consideraciones, las ecuaciones se reducen a:

Por lo tanto, 0 y Zo es real (puramente resistiva).

En lo que se refiere a la impedancia de entrada vista desde el generador en dirección a la carga, la ecuación general (2-35) se reduce, 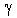= j, a:

y como tanhjßl = (0 + jtanßl)/(1+0) = jtanßl, la ecuación anterior queda finalmente de la forma:

en donde l es la longitud total de la línea.

A continuación procederemos a utilizar la ec. (2-50) para los dos casos especiales en que la línea termina en corto circuito o en circuito abierto.

a) Línea teminada en corto circuito
En este cso ZL = 0 y la ec. (2.50) se reduce a:

b) Línea terminada en circuito abierto
Ahora ZL -> y la ec. (2-50) toma la forma:

Las ecuaciones muestran que cuando una línea sin pérdidas de longitud arbitraria t termina en corto circuito o en circuito abierto, la impedancia de entrada es puramente reactiva (jXl). En cualquiera de los dos casos, la reactancia puede ser inductiva o capacitiva, dependiendo del valor de ßl, ya que las funciones tan ßl pueden tomar valores positivos o negativos.

En la práctica, no es posible obtener una línea realmente terminada en circuito abierto (impedancia de carga infinita), ya que existen problemas de radiación en el extremo abierto, especialmente a latas frecuencias, y acoplamiento con objetos cercanos. Sin embargo, es interesante notar que las reactancias de entrada de líneas terminadas en circuito abierto o en corto circuito son idénticas cuando sus longitudes difieren entre sí por un múltiplo impar de /4. En la figura se muestran algunas secciones de línea, ilustrando su equivalencia con una inductancia o una capacitancia, a una frecuencia determinada.

Líneas desacopladas y Ondas Estacionarias
Si = 0, la línea esta acoplada, porque ZL=Zo, pero si por el contrario no es igual a cero se dice q la línea esta desacoplada. El objetivo de un ingeniero en transmisión es lograr que sea muy pequeña, de modo que la potencia transferida a la carga sea máxima. Por lo general, un acoplamiento se considera aceptable si , con lo cual se entrega a la carga aproximadamente el 96% de la potencia incidente. Veamos ahora cómo es la onda de voltaje total a lo largo de una línea desacoplada
Para cualquier z, la magnitud del voltaje total se puede obtener a partir de la ecuación

En general el coeficiente es complejo y se representa ahora como :

Por lo tanto, suponiendo que =0, la expresión para la magnitud del voltaje total toma finalmente la forma:

Esta función se puede graficar fácilmente. Considerando que los valores extremos de dicha función son:

De allí que la onda de voltaje tenga como valor máximo y como mínimo un valor igual a Su gráfica se muestra en la figura a continuación:

El patrón de la onda total de voltaje es periódico y se denomina patrón de onda estacionaria, pero resulta interesante (y siempre debe recordarse) que su período es diferente al de la onda incidente. La onda incidente y la reflejada tienen un período de z, mientras que la onda total (superposición de dos ondas anteriores) tienen un período de 2z. Es decir, que si la onda incidente tiene una longitud de onda , entonces la onda estacionaria tendrá una longitud de onda e = /2.

La expresión matemática de la onda estacionaria de corriente es la siguiente:

Al cociente del voltaje máximo de la onda estacionaria sobre el voltaje mínimo se le da el nombre de relación de onda estacionaria, ROE o VSWR:

Ahora bien, si se efectúa el cociente del voltaje máximo sobre la corriente mínima (ambos están en el mismo punto sobre la línea), es obvio que se obtendrá el valor de la impedancia vista en ese punto hacia la carga:

Similarmente, para un punto donde el voltaje sea mínimo, la corriente será máxima y se tendrá:

Como Zo es real, ambas impedancias dadas por las dos ecuaciones anteriores también son puramente resistivas.
Conviene observar detalladamente el comportamiento del coeficiente de reflexión a lo largo de la línea, por lo que es también posible definirlo para otros puntos de la línea de la manera siguiente:

esta ecuación se puede rescribir con 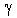= j, como:

De la ecuación anterior se deduce que el lugar geométrico en el plano complejo del coeficiente de reflexión de voltaje es un círculo de radio || y se repite cada vez que se avanza e o /2 a lo largo de la línea.

Bibliografía

RODOLFO NERI VELA. Líneas de Transmisión. Editorial McGraw-Hill Interamericana. Noviembre de 1999. México. Páginas: 1, 2, 51 - 78

MELANIO CASTILLO. Guía de Laboratorio de Líneas de Transmisión y Antenas.