Test Equipment.

The Neglected Q Meter.

This article covers the full range from the theory of tuned circuits and Q to repair tips for that battered Q meter you bought on eBay. Feel free to skip sections if the math gets a little deep for your tastes. My goal is to answer any question anyone may have about a Q meter, what it is for, and how to use it.
If you have a manual you probably will decide to skip the operation and calibration sections. The passage of time requires an additional step in the calibration that Boonton did not plan on. To wind up with an accurately calibrated instrument you must read and perform the first section of the calibration procedure given on this page.
Contents.
Tuned Circuits and Q.
Q Meter Circuit and Theory.
How Inductance is Measured.
Before Turning on the Power.
Basic Q Meter Operation.
Advanced Measurement.
Repairing Q Meters.
Calibration.
The Line Voltage Stabilizer.
Useful Accessories.

Tuned Circuits and Q.

What is Q?
Q is the quality factor of a tuned circuit. The higher the quality the narrower is the bandwidth.
What is a tuned circuit?
At frequencies from low audio up through the VHF (very high frequency) range, 30 Hz to 300 MHz, tuned circuits are made of a coil of wire known as an inductor and a capacitor. An ideal tuned circuit would have perfect quality and would pass just one frequency and discriminate against all others. There's no such thing as perfection so a tuned circuit passes a band of frequencies. The width of this band is compared to the center frequency is a measure of Q.

Figure 1, Frequency response of a series tuned circuit.

For a verbal description click here.

A tuned circuit is made less than perfect by resistance. Almost all of this resistance is in the wire that makes up the coil. The capacitor that is part of the tuned circuit has very little losses so the coil is where the blame is placed. The Q of a coil can be calculated before it is teamed up with a capacitor to make a tuned circuit.
Q = XL / R
Where XL is the reactance of the inductor at the resonant frequency and R is the series resistance of the coil.
Where did this equation come from? Was it handed down from the mountain top on a stone tablet? I don't think so.
One of my professors at U of F had graduated from MIT in 1918. He told us that PhD students at that time and place were working on series resonant circuits. Sophomore physics and electrical engineering students analyze those circuits in laboratory experiments. Now I am going to engage in a little historical speculation. I suspect that one of those PhD dissertations covered Q of a resonant circuit. The result was probably Q = fr / (f2 - f1), and Q = X_L / R. As the state of the art improved through the 20s and 30s the frequencies became so high that conventional coils and capacitors no longer worked. They would have started using strip lines and resonant cavities. So how do you calculate Q when there is not an inductor in sight. Q had to be redefined to be more general. The definition someone came up with is as follows.
Q = (energy stored on each signal cycle) / (energy lost during 1 radian of the cycle).
Read the equal sign as the three line sign meaning "is defined as". I'm sure some reverse engineering went in to this definition so it wouldn't contradict the original one. Here is how we get from the above definition to the one we all know and love.
Starting with a series resonant circuit the energy stored is continuously swapped back and forth between the inductor and capacitor. From fundamental electricity we know that the energy stored in a capacitor and an inductor are,
W_C = V^2 C / 2
And
W_L = I^2 L / 2
Where W is the amount of energy stored in either the capacitor or inductor according to the subscript, V is the voltage across the capacitor, C is the capacitance of the capacitor, I is the current through the inductor, and L is the inductance of the inductor. The stored energy is being traded between the inductor and capacitor and It may be hard to get a handle on it. What we must do is to order time to stop at the instant when the energy in the inductor is at its maximum value. Since this is a thought experiment we don't need a DeLorean to make that happen. We stop time at the peak value of the current. Since this is a series circuit by Kirchhoff's law the current is the same in all components. In our simple circuit the energy lost is dissipated by the resistor and we can write,
W_L = (I_P^2 L) / 2
And
P_R = I_RMS^2 R
We need the two currents to be the same so they will cancel out in the final equation.
I_RMS = I_P / sqrt(2)
Substituting for I_RMS into the equation for P_R gives.
P_R = (I_P / sqrt(2) )^2 R.
Since (sqrt(2))^2 = 2 we have,
P_R = I_P^2 R / 2.
Energy = Power times Time so as explained above we need to find the energy dissipated by the resistor in one radian of time. One radian is the period, time for one cycle given as the symbol T, of the wave divided by 2pi because there are 2 pi radians in one cycle. Furthermore the period, T = 1/ f so one radian = 1 / (2 pi f). Where have we seen that one before?
So, the energy dissipated in a resistor in 1 radian of time is,
W_R = I_P^2 R / (4 pi f)
Now if we divide W_L by W_R we have,
Q = (I_P^2 L / 2) / (I_P^2 R / (4 pi f))
Let's do some obvious canceling.
Q = L / (R / (2 pi f))
Inverting the divisor and multiplying gives,
Q = 2 pi f L / R
Since 2 pi f L = X_L we have,
Q = X_L / R.
So now we have a proven formula for calculating Q based on the reactance of the inductor at the resonant frequency and the resistance of the coil. Just one little problem. If we use an ohmmeter to measure the resistance the calculation of Q will be much higher than it in fact is. At radio frequencies the current in a wire tends to flow near the surface of the wire rather than being evenly distributed through the volume of the wire. The higher the frequency the more pronounced this effect is. It is called the skin effect. Skin effect causes the effective resistance of the coil, or any wire to rise at higher frequencies.
Bandwidth and Q.
To investigate the relationship between bandwidth and Q we will use a series tuned circuit. The reason is, it's much easier that way. Although almost all of the tuned circuits used in radio equipment are parallel tuned circuits they are much more difficult to analyze.
The reason is how the inductor behaves. A real inductor will show some resistance at zero frequency (DC) and infinite impedance at infinite frequency. Well, not true because capacitance between the turns of the coil gets in the way. The impedance of the coil is high at some arbitrarily high frequency. The standard model for a coil is to think of it as a perfect inductor in series with a perfect resistor.
If we try to model a parallel tuned circuit (Coil and capacitor connected in parallel) we model the coil as an inductor in parallel with a large resistance. Such a model has zero impedance at zero frequency and the value of R at high frequencies. Real world coils come much closer to the behavior of the series model. So in a series tuned circuit the capacitor, the inductor, the resistance of the coil, and any resistance we may add in the form of a discrete resistor will all be in series. In accordance with Kirchhoff's current law every component will have the same current flowing in it.

Figure 2, Schematic diagram of a series tuned circuit and its phasor diagram.

For a verbal description click here

n The phasor diagram next to the circuit diagram illustrates the phase relationship between the voltages across each of the elements in the circuit. The current in the circuit is given by
i = v / Z
Where i is the ac current in the circuit in amps, v is the applied ac voltage in volts, and Z is the impedance in ohms which is given by,
Z = sqrt(R^2 + (2 pi f L - 1 / (2 pi f C))^2).
Where f is the frequency in hertz, R is the total circuit resistance in ohms, L is the inductance in henrys, and C is the capacitance in farads.
We want to find the two frequencies f1 and f2 where the current is down to 1 / sqrt(2), 0.707, -3 dB, referenced to the current at the resonant frequency, fr. This derives from this equation.
Q = fr / (f2 - f1)
Where fr is the resonant frequency, peak of the curve above, f1 is the lower 0.707 point, and f2 is the upper 0.707 point. We will derive expressions for f1 and f2 and then using nothing more than algebra arrive at,
Q = XL / R
We can simplify the math a bit by removing reference to the current and the applied voltage and work directly with the impedance Z. If the voltage is constant and the current is down to 1 / sqrt(2) the impedance must be up to sqrt(2).
Resonance is defined as the frequency where XL = XC or 2 pi f L = 1/(2 pi f c). In the equation for impedance above if the condition of resonance is met the second squared term under the radical will be zero. Thus the impedance Z will be Z = sqrt(R^2) = R. For the impedance to be sqrt(2)R the second term must be equal to R. Thus,
Z = sqrt(R^2 + R^2) = sqrt(2R^2) = sqrt(2)R.
Using the simpler form of impedance we write,
Z = sqrt(R^2 + (XL - XC)^2)
By inspection we can see that if XL increases by 0.5 R and XC decreases by 0.5 R the impedance will be sqrt(2)R. Just one little problem. XL and XC don't change at the same rate. The graph of XL versus frequency is a straight upward sloping line while the graph for XC versus frequency is a parabola. If we look at a parabola over a small enough frequency span it looks like a straight line but when the Q of the circuit is low this approximation no longer holds.
So we set the reactance expressions at f1 and f2 equal to R and ignore the radical as follows. The equations below are based on the rule "If a^2 = b^2 then a = b" except for a slight matter of signs which we will be aware of as we write the equations.
-R = 2 pi f1 L - 1 / (2 pi f1 C)
And
R = 2 pi f2 L - 1 / (2 pi f2 C)
The frequency f1 is below the resonance point and the inductive term is smaller than the capacitive term so R must be negative to be equal to the reactive term. The frequency f2 is above the resonance point and the inductive term is larger than the capacitive term so R must be positive to be equal to the reactive term. In the impedance equation squaring the terms takes care of signs and we don't have to be concerned about them. In these equations we do. Now we multiply through by 2 pi fC in both equations.
-2 pi R C f1 = 4 pi pi L C f1^2 - 1
and
2 pi R C f2 = 4 pi pi L C f2^2 - 1
Now we rearrange these equations to get them into the classic quadratic form.
-4 pi pi L C f1^2 - 2 pi R C f1 + 1 = 0
and
-4 pi pi L C f2^2 + 2 pi R C f2 + 1 = 0
The next step is to plug the values into the quadratic formula and turn the crank. But I wanted some kind of check on the reliability of these equations. I used an example from the electronics textbook.
L = 79.58 millihenrys,
C = 318.3 Nano farads, and
R = 50 ohms.
XL = XC = 500 ohms, and
fr = 1,000 Hz.
The Q of the circuit by Q = XL / R = 10. By Q = fr / (f2 - f1) , (f2 - f1) = 100 Hz.
Entering the quadratic formula into an Excel cell and spending a couple of hours trying to find the typo that kept the answer from coming out right, yielded, f1 = 951.2 Hz and f2 = 1051.2 Hz. The asymmetry of the f1 and f2 points is caused by the parabolic shape of the capacitance reactance curve which I spoke of above. Even when a resistor of 250 ohms is inserted giving a Q of 2 the bandwidth comes out right.
I used to be under the mistaken impression that the formula Q = fr / (f2 - f1) was an approximation That would fall apart at low values of Q. Also I believed it could not be derived. In fact I have never seen a derivation or proof of the validity of this formula. It's a little harder to invent the wheel when you have never seen one.
Something very important I learned from the example is that the correct answer is given by using the positive sign on the radical in the quadratic formula. When the negative sign is used the frequency is given as a negative number. Since there is no such thing as negative frequency the positive one has to be the right answer.
Well, let's grind out some more algebra. Isn't this fun?
X = (-b +/- sqrt(b^2 - 4ac)) / (2 a)
-4 pi pi L C f1^2 - 2 pi R C f1 + 1 = 0
f1 = (2 pi R C + sqrt((- 2 pi R C)^2 + 16 pi pi L C )) / ( -8 pi pi L C )
-4 pi pi L C f2^2 + 2 pi R C f2 + 1 = 0
f2 = (-2 pi R C + sqrt((2 pi R C)^2 + 16 pi pi L C ))/ ( -8 pi pi L C)
Now we subtract f1 from f2. The denominators are the same so there is no need to worry about finding a common denominator. The radical has the same value so it will go away. The b coefficient has a different sign in the two but the squaring operation makes it all positive. So it looks like we get,
f2 - f1 = (-2 pi R C -(2 pi R C)) / ( -8 pi pi L C) = -4 pi R C )/ (-8 pi pi L C )
f2 - f1 = R / ( 2 pi L )
This seemingly simple equation does produce correct answers when the values from the numerical example are inserted into it.
Now we have to divide fr by f2 - f1. This will produce the value of Q. We know that fr = 1 / (2 pi sqrt of ( L C )). What was that rule? Oh yes, invert the divisor and multiply.
Q = (( 2 pi L ) / R )( 1 / ( 2 pi sqrt(LC))
Q = (2 pi L ) / ( R (2 pi sqrt(LC)))
Q = L / (R sqrt(LC))
This equation also gives the correct numerical answer. Now, we are sorry we cancelled those 2 pi terms. Let's put them back by multiplying by (2 pi) / (2 pi)
Q = (2 pi L ) / (R 2 pi sqrt(LC))
but,
fr = 1 / (2 pi sqrt(LC)
so
Q = (2 pi fr L ) / R
Since 2 pi fr L = XL we have,
Q = XL / R
QED
There, that didn't hurt so bad, did it.
Q Meter Circuit and Theory.
The Q meter may be one of the simplest pieces of test equipment in existence. It has 3 basic parts, an oscillator, a calibrated variable capacitor, and an RF voltmeter.
The Boonton Q Meter.

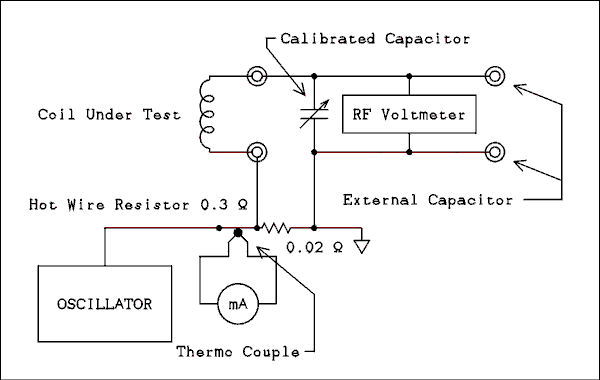
Figure 3,Functional Block Diagram of the Boonton Q Meter.

For a verbal description click here.

In the Boonton 160 and 260 Q meters the oscillator operates from 50 kHz to 50 MHz. There is a Boonton model 190 which I have never seen in the flesh that covers from 20 MHz to 250 MHz. The output of the oscillator is taken from a very low impedance winding on the coil and fed to the series combination of the hot wire 0.3 ohm resistor and the 0.02 ohm injection resistor.
To allow for accurate testing of circuit Q the voltage that is applied to the test circuit must be well known. The hot wire resistor as its name implies gets hot when a current passes through it. The hot wire heats the thermocouple which is made up of two dissimilar metals. When heated the thermocouple generates a small voltage but because it has a low resistance can supply a relatively large current. The milliammeter indicates this current and makes it possible for the user to adjust the oscillator output to the same level for every measurement which is usually 1 amp.
This current of 1 amp causes a voltage of 20 millivolts (mv) to appear across the 0.02 ohm resistor. (In the 160 the resistor is 0.04 ohms and the voltage is 40 mv). This is the source voltage for the test circuit. It is both constant and has a very low impedance. When a coil is connected to the test terminals and the frequency of the oscillator and calibrated capacitor are properly adjusted the combination of the capacitor and coil form a series resonant circuit. The current through the circuit can be as much as several 10s of milliamps which can produce a relatively large voltage across the capacitor.
Note: The RF voltmeter is measuring the voltage across the capacitor but it is also measuring the voltage across the coil plus the 20 mv excitation voltage.
The Heath Q meter.

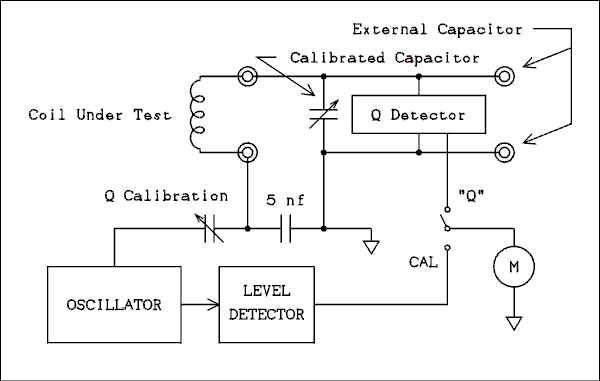
Figure 4, Functional Block Diagram of the Heath Q Meter.

For a verbal description click here.

The Heath engineers used a very different system for injecting the signal into the tuned circuit. It would not have been economically feasible to use the hot wire resistor - thermocouple - 0.02 ohm resistor system. It is doubtful that kit builders could have successfully installed these components. Instead they used a capacitive voltage divider system. The five nf injection capacitor was especially manufactured. It consists of alternating layers of copper and mica held together by a plastic screw.
In the Heath Q meter the oscillator tunes from 150 kHz to 18 MHz. Heath used a different method of injecting the signal into the tuned circuit. Their front panel labeling makes inside information a little confusing so pay close attention. The oscillator output is from a cathode follower which could not drive a 0.3 ohm resistance. Instead it drives a capacitive voltage divider made up of the small trimmer capacitor labeled in the diagram as Q Calibration and a 5 nf fixed capacitor. This is an internal calibration adjustment. Heath supplied an inductor with inductance and Q printed on it. This was how the user calibrated the instrument. Note: No doubt the calibration coil was measured on a Boonton 260.
The oscillator level is set by changing the front panel switch to the CAL position. This has nothing to do with the adjustment of the trimmer capacitor. A front panel control is adjusted to bring the meter pointer to either of the X1 or X2 MULTIPLY Q BY marks. The oscillator has its own level detector which is connected directly to the meter movement. After the oscillator level has been set the switch is changed to the "Q" position. In this position the meter movement is connected to the RF voltmeter circuit which is not unlike the circuit of a VTVM.
The RF voltage developed across the 5 nf capacitor is the excitation voltage for the tuned circuit.
The advantage of the circuits used by Heath is there is no fragile thermocouple to be burned out if the oscillator level is allowed to get too high.
General information for Both Q Meters.
The RF voltmeter measures the voltage across the capacitor which is directly proportional to the Q of the circuit. The voltage it measures is Q times the excitation voltage. In the Boonton 160 the resistor is 0.04 ohms so the excitation voltage is 40 mv. The Boonton 260 uses an excitation voltage of 20 mv and in the Heath Q meter the excitation voltage is dependent on the sensitivity of the RF voltmeter circuit. The current through the test circuit at resonance is,
i = vex / r
Where i is the current, vex is the excitation voltage, and r is the resistance of the coil, shown as a lower case letter because it is not a physical resistor. The voltage across the capacitor is,
vc = i XC
Where vc is the voltage across the capacitor and XC is the reactance of the capacitor. Substituting the second in to the first we have,
vc = vex XC / r
At resonance XC = XL so XL may be substituted into this equation to obtain,
vc = vex XL / r
r is the resistance of the coil and,
Q = XL / r
Thus,
vc = vex Q
Or
Q = vc / vex

How Inductance is Measured.
The Q meter can be used in two ways to measure inductance and Q.

The frequency of the oscillator can be set to certain specific frequencies in accordance with a table printed on the instrument case which will allow the inductance to be read on a scale on the capacitor dial. The user is responsible for assigning the decimal point to the proper place.
The frequency of the oscillator can be set to the eventual operating frequency of the tuned circuit for example 455 kHz. When the voltmeter is peaked the dial reads out the capacitance necessary to tune the coil to that frequency. The meter then indicates the Q of the circuit at that frequency.

Even though the characteristics of the coil are measured in series resonant mode a capacitor of the proper value may be connected in parallel with the coil to make a parallel resonant circuit and the Q, bandwidth, and resonant frequency will be the same as measured on the Q meter.
The External Capacitor terminals on the Q meter are to allow the connection of an external fixed capacitor to extend the capacitance range. Also a high Q coil known in Q meter lingo as a work coil may be connected to the coil terminals and the value of an unknown capacitor can be measured. There are many other things that can be done with a Q meter. They will be described in the "Advanced Measurements" section.
Before Turning on the Power.
OK. So you bought a Q meter from someone and the package has arrived on your doorstep. You are dying to see if it works. But if you plug it in and turn it on you could turn a relatively easy repair job into a more complex and expensive one. As with any old equipment it is not advisable to just plug it in and turn it on. Skip down to the Repairing Q Meters section below. If you disregard this advice and the Q meter smokes after being turned on, don't come crying to me.
Basic Q Meter Operation.

If you've operated one Q meter you have operated them all. Actually there aren't that many models available. I don't think any manufacturer is making one at the present time. The three in the picture are a Heathkit model QM-1, A Boonton 260, and a Boonton 160. There is a Boonton model 190 which I do not have. It covers the frequency range from 20 to 250 MHz.
Operating the Boonton Q Meter.
Note: The Boonton 160 and 260 are very similar. The most important difference from the standpoint of operation is that the 160 has no LOW Q and DELTA Q settings. Everything else is similar enough as to not require a separate set of instructions.
Turning on the power.
The on/off switch is on the XQ COARSE in the same way that the on/off switch is on the volume control of a radio. Turn the knob just far enough to hear and feel the click. The red power indicator lamp will come on. Do not turn the XQ COARSE control any farther up at this time.
Setting the Measurement Frequency.
If you are changing the frequency after making a measurement be sure to set the XQ COARSE control to minimum without turning off the instrument before changing the frequency dial or band switch.
The band switch selects the frequency ranges. Select the one that contains the frequency you want to use.
The frequency dial tunes the oscillator over the range set by the band switch. Tune the dial to the desired frequency. Be sure to read the scale corresponding to the band you have selected.
Zeroing the Q METER.
Note: This adjustment should be made with the oscillator level set to minimum. Turn the XQ COARSE level as far counterclockwise as possible without turning the instrument off. Turn the XQ FINE control as far counterclockwise as possible. Connect the unknown coil to the COIL terminals of the Q meter. The meter zero point will change if there is no coil connected. Adjust the Q ZERO ADJUST to bring the pointer to zero on the Q scale. Press the lever switch down to the low Q position. While continuing to hold the lever down check the meter zero again and if necessary make a fine adjustment to bring it to zero. Release the lever switch. Recheck this setting before making a critical measurement of Q.
Setting the Oscillator Level.

----------**********WARNING**********----------
THE HOT WIRE RESISTOR AND THERMOCOUPLE ASSEMBLY CAN BE EASILY DAMAGED BY SETTING THE OSCILLATOR LEVEL TOO HIGH. This is especially true of the 160. Although you will get the most accurate readings of Q when the MULTIPLY Q BY meter is set to one it is safer to set it to 1.5 or 2. If you are making measurements of inductance or resonating capacitance and the value of Q is not highly important to the measurement the MULTIPLY Q BY meter should be kept around 2.
The XQ COARSE and XQ FINE controls set the oscillator level. Because the current is sensed by a thermocouple measuring the temperature of a hot wire the response can be slower than you might expect. Move the control and wait for the meter to move to its new reading and stop moving. Sudden large movement of the XQ COARSE control can leave you with a burned out thermocouple and no source of replacement parts. After you get close to the desired setting with the XQ COARSE control use the XQ FINE control to arrive at the final setting.
Measuring Q and Inductance or Capacitance.
Check to see that the fine (vernier) MMFD dial is set to zero. If not set it. Turn the capacitance/inductance dial slowly while watching the Q METER. When the meter reads upscale carefully adjust the dial for maximum reading. Read the value of Q on the Q scale of the meter. For the safety of the thermocouple turn down the oscillator after reading the Q. Do not turn the instrument off.
If you have a 260 and the meter reads below 60 depress and hold the LOW Q lever. Check the tuning of the dial to be sure it is tuned exactly to the peak. While continuing to hold the LOW Q lever read the Q on the LOW Q scale of the meter. You may release the lever after reading the value of Q. For the safety of the thermocouple turn down the oscillator after reading the Q. Do not turn the instrument off. The delta Q position of the lever will be covered in the advanced measurements section.
Reading Capacitance.
The MULTIPLY Q BY meter does not have to be reading upscale while you read the capacitance/inductance dial. It is recommended that you turn down the oscillator level without turning the instrument off.
The capacitance scale on the capacitance/inductance dial reads the resonating capacitance for that inductor at the measurement frequency. If the fine dial is not on zero add or subtract its setting to/from the main capacitance dial reading. The dial reads directly in MMFD which stands for micro microfarads. 1 MMFD = 1 pf. This was the standard way of measuring small capacitances when this instrument was manufactured. This was before the Pico farad was invented.
Reading Inductance.
The inductance scale reads from .9 to 13. To properly interpret the value of the inductor you must Properly position the decimal point in the number. For example, suppose the dial reads 5.6 and the oscillator is set to 2.5 Mc (MHz). The table on the front of the instrument informs us that the inductance range is from 10 to 100 microhenrys. The scale reading must be multiplied by 10 uh to obtain the inductance value. The measurement range is actually from 9.0 to 130 uh. Obviously the reading can't be 5.6 microhenrys. The reading is 56 uh. Interpretation is fairly straight forward most of the time. Be careful if the reading is 1.1 or 11. In the above example a reading of 1.1 would be 11 uh and a reading of 11 would be 110 uh.
Operating the Heath/Heathkit Q Meter.
Note: There are several significant operating differences between the Boonton and the Heath Q meters. A separate set of instructions is given for the Heath.
Turning on the power.
The on/off switch is on the SET LEVEL control in the same way that the on/off switch is on the volume control of a radio. Turn the knob just far enough to hear and feel the click. The green power indicator lamp will come on. Do not turn the SET LEVEL control any farther up at this time.
Setting the Measurement Frequency.
The band switch selects the frequency ranges. Heath labeled the band switch only with A, B, C, and D. You must look at the scales on the frequency dial to decide which band you wish to select. Select the one that contains the frequency you want to use.
The frequency dial tunes the oscillator over the range set by the band switch. Tune the dial to the desired frequency. Be sure to read the scale corresponding to the band you have selected.
Zeroing the Q METER.
Note: This adjustment should be made with the oscillator level set to minimum. Turn the SET LEVEL control as far counterclockwise as possible without turning the instrument off. Connect the unknown coil to the COIL terminals of the Q meter. The meter zero point WILL change if there is no coil connected. Set the CAL - "Q" switch to the "Q" position. Adjust the SET ZERO control to bring the pointer to zero on the Q scale. Recheck this setting before making a critical measurement of Q.
Setting the Oscillator Level.
Change the CAL - "Q" switch to the CAL position. Adjust the SET LEVEL control to bring the pointer over either the red X1 or X2 MULTIPLY Q BY marks on the meter face. The only reason to use the X2 mark is if you have a coil with a Q greater than 250, the maximum reading on the Q scale. There is nothing in this instrument that can be damaged by setting the oscillator level too high. For the vast majority of measurements you will leave the level set to the X1 mark.
Measuring Q and Inductance or Capacitance.
Change the CAL - "Q" switch to the "Q" position. Check to see that the VERNIER knob is set to zero. If not set it. Turn the capacitance/inductance dial slowly while watching the meter. When the meter reads upscale carefully adjust the dial for maximum reading. Read the value of Q on the Q scale of the meter.
Reading Capacitance.
The C_E scale on the capacitance/inductance dial reads the resonating capacitance for that inductor at the measurement frequency. If the VERNIER knob is not on zero add or subtract its setting to/from the main capacitance dial reading. The dial reads directly in MMFD which stands for micro microfarads. 1 MMFD = 1 pf. This was the standard way of measuring small capacitances when this instrument was manufactured. This was before the Pico farad was invented. When the instrument is being used to measure capacitance the C_T scale must be read.
Reading Inductance.
The inductance scale reads from 1.0 to 11. To properly interpret the value of the inductor you must Properly position the decimal point in the number. For example, suppose the dial reads 5.6 and the oscillator is set to 2.5 Mc (MHz). The table on the front of the instrument informs us that the inductance range is from 10 to 100 microhenrys. The scale reading must be multiplied by 10 uh to obtain the inductance. Obviously the reading can't be 5.6 microhenrys. The reading is 56 uh. Interpretation is fairly straight forward.
Advanced Measurement.
You can do more with a Q meter than measure Q and inductance. These measurements will be described here as given in the Boonton and Heathkit manuals.
Boonton Q meter.
Some of these measurement techniques may be transferred to the Heathkit and some may not be possible with that instrument. It will depend on the ingenuity of the user.
Extending the Inductance Range.
To change the inductance range by a factor of n you must change the frequency by a factor of sqrt(n). The 2.5, 7.9, 25 sequence goes by the sqrt(10) which changes the inductance range by a factor of 10. There is no immutable law that says you can only change the frequency by the sqrt(10). The next lowest inductance range is 1 to 10 Millihenrys (mh). The frequency for this is 250 kHz. If you reduce the frequency by a factor of 5 to 50 kHz the inductance range is multiplied by 25 and it is 25 to 250 mh.
On the other end the highest frequency listed for inductance is 0.1 to 1.0 microhenrys (uh) at a frequency of 25 MHz. The frequency dial on the highest band has markings out to 53.5 MHz. If the frequency is set to 50 MHz the square of the frequency ratio is 4. When a 2-1/2 length of number 22 hookup wire is connected between the coil terminals without looping it into a coil the inductance dial reads 2.3. The inductance is this number divided by 40 since the divisor for 25 MHz is 10. The inductance is then 0.0575 uh with a Q of 39.5. You should consult the "Sources of Error" section of the 260 manual before taking this value as gospel.
Measuring the Distributed Capacitance of a Coil, Preferred Method.
Capacitance is always with us. A coil of wire has capacitance between the turns and at some frequency this capacitance will resonate with the inductance to form a parallel resonant circuit. This is called the self resonant frequency of the coil because it forms a resonant circuit with no added components. This method of determining the distributed capacitance starts with finding the self resonant frequency of the coil. This in itself is useful information.

Set the Capacitance/Inductance dial to 400 MMF (pf). This is C1 for calculations below.
Connect the Coil Under Test (CUT) to the COIL terminals of the Q meter. If you know the inductance of the coil you can calculate the frequency by this equation.
f1 = 1/(2 pi sqrt(LC))
Where C = 400 e-12 farads. If you don't know the inductance of the coil it is suggested that you use the Q meter to measure it according to instructions given above. After calculating the frequency tune the oscillator to this frequency and move the dial around until you find the peak on the Q meter. Record this frequency as f1.
Now we will find the self resonant frequency of the coil. Change the oscillator frequency to 10 times the value of f1. Replace the CUT with a work coil capable of being tuned to resonance by the capacitor at the new frequency.
Adjust the Capacitance/Inductance dial for resonance with the work coil. If you are prone to forgetting things, write down the capacitance reading.
Connect the CUT to the CAP terminals on the instrument while leaving the work coil in place on the coil terminals.
Retune the Capacitance/Inductance dial to resonance. If the capacitance was increased by this tuning increase the frequency. If the capacitance was reduced, decrease the frequency. Find the frequency where the capacitance dial reads the same as it did with the work coil by itself. Write down the frequency and call it f0.
The distributed capacitance Cd is given by,
Cd = C1 / ((f0/f1)^2 -1)
If you enter C1 in pf the resulting value of Cd will also be in pf.

Distributed Capacitance Without a Set of Work Coils.
The above method is fine if you have a complete set of Boonton work coils. But if you don't there are other methods that don't require a work coil. The below procedure gives best results for values of Cd larger than 10 pf. The error is approximately +/- 2 pf.

Set the capacitance dial to 50 pf. Call this C1.
Connect the CUT to the Coil terminals and adjust the oscillator frequency to the resonance. Record this frequency as f1.
Change the oscillator frequency to a lower frequency of f1/n. n may be any real number greater than 1 but less than or equal to 3. Record the new frequency as f2.
Increase the capacitance dial to find the new resonance at this new frequency. Record this as C2.
Calculate the distributed capacitance by,
Cd = (C2 - n^2 C1)/(n^2 - 1).
Note that if n = 2 this equation simplifies to,
Cd = (C2 - 4C1)/3.

An average taken with different values of C1 and n will improve the accuracy.

Once you know the distributed capacitance of a coil you can correct the measured inductance. When the inductance is measured the distributed capacitance makes the inductor appear larger than it actually is. For inductance measurements this becomes important only when the distributed capacitance is significant compared to the capacitance of the resonating capacitor, (the reading on the capacitance scale at the setting where the inductance is measured). The dial may be used as a circular slide rule to calculate the effective inductance.

Follow the procedure way above to measure the inductance.
Turn down the oscillator level as the meter reading is no longer important.
Read the capacitance scale and call the reading C.
Add the distributed capacitance, Cd, to the capacitance scale reading C.
Move the dial to set the sum on the capacitance scale. The inductance now indicated on the inductance scale is the true inductance of the coil.

If the value of Cd is 6 pf and the capacitance scale reads 400 pf the error is only 1.5%. However if the value of Cd is 15 pf and the capacitance scale reads 45 pf the error is 25%. You must judge when to correct and when not to correct.
Parallel Measurements.
The Q meter can be used to measure the true resistance and reactive component of resistors and the value of small capacitors. All require a set of work coils and calculation to obtain the value. That's probably the reason that Boonton developed the 250 RX meter. If you don't have an RX meter and do have a Q meter you may want to know how to do these measurements. But you still need a set of work coils. In case you want to roll your own they range from 1 microhenry to 25 millihenrys. There are 14 of them set in a 1, 2.5, 5, 10, sequence. They do turn up on eBay now and then. You just have to keep watching.
I will give the procedure for using the delta Q feature of the 260. Once you know that you can make any parallel or series measurement you want to.

Connect a work coil to the COIL terminals and tune the Capacitance/Inductance dial for resonance.
Set the outer knob of the delta Q knob so its dial reads approximately the same value as the reading on the Q meter.
Lift the delta Q lever key to the delta Q position. While continuing to hold the lever, adjust the fine delta Q, inner knob, for a reading of zero on the red delta Q scale. Check the tuning of the capacitance dial and if necessary readjust the fine delta Q control. Release the lever key.
Make the change such as connecting a resistor or capacitor to the CAP terminals of the instrument or connect a resistor in series with the work coil.
Readjust the capacitance/inductance dial and again lift the lever key to the delta Q position.
Make a fine adjustment of the capacitance and read the change in Q from the red meter scale. Release the lever key.
The parameters of a resistor connected in parallel with the test circuit, connected to the CAP terminals are given as follows.
Rp = (Q1Q2) / (2 pi f C1 delta Q)
Where Rp is the effective resistance of the resistor at the test frequency, Q1 is the Q measured before the resistor was connected, Q2 is the Q measured after the resistor was connected, delta Q is the change in Q when the resistor was connected, f is the frequency of the oscillator, and C1 is the reading on the capacitance scale before the resistor was connected. If delta Q is very small, better accuracy can be achieved if Q2 is obtained by subtracting delta Q from Q1.
If the resistor is capacitive the value of C is,
Cp = C1 - C2
Where C1 is the reading on the capacitance dial before the resistor was connected, and C2 is the reading after the resistor is connected. If the value of Cp is negative from the above formula the resistor is inductive.
If the latter is true the inductance is,
Lp = 1 / (4 pi^2 f^2 (C2 - C1))
Where C1, C2, and f, are as defined above.
Series Measurements.
Boonton recommends that when a resistor is to be connected in series with a coil that the connection be made and a shorting strap used to short out the resistor for the initial measurement. The strap is removed to make the measurement involving the resistor. Values that are subscripted 1 are with the resistor shorted out and values that are subscripted 2 are with the resistor effectively in series with the coil.
Rs = ((C1 / C2) Q1 - Q2 ) / (2 pi f (C1 Q1 Q2)
And
Ls = (C1 - C2) / (4 pi^2 f^2 C1 C2)
or
Cs = (C1 C2) / (C2 - C1)
If you intend to use any of these equations frequently you should; 1) make an Excel spreadsheet with the formulas programmed into cells with clear heading labels, or, 2) program the equations into a programmable calculator, or, 3) if you have and know how to use visual basic write a program with everything in it complete with on screen documentation.
Heath Q meter.
Earlier on this page I said if you've operated one Q meter you've operated them all. That is pretty much true. The above procedures for the Boonton can NOT be done on the Heath. The only exception is measurement of capacitance. The Heath circuit connects a detector diode to the high side of the coil but the resulting DC gets to the DC amplifier through the coil under test. Any low DC resistance connected across the CAP terminals will disrupt the DC levels and render the Q readings inaccurate or in the case of a coil having a few ohms the meter will never move from zero.
Also the Boonton work coils can't be used with the Heath meter. In the Boonton Q meter the low end of the work coil is connected to ground through a very low impedance, namely 0.02 ohms. In the Heath The low end of the coil goes to ground through a 5000 pf capacitor in parallel with a total of 6.6 megohms of resistance. The Boonton work coil is a big antenna which picks up every line related signal to which the voltmeter circuit has no immunity. Grounding the shell of the work coil adds so much capacitance as to render the work coil unusable. Boonton does not recommend it.
If a low profile coil such as the RF choke supplied for calibration is used the Heath Q meter can be used to measure small values of capacitance.
Repairing Q Meters.
My very first Q meter was a Boonton 160 obtained in 1969. When I turned up the oscillator signal there was no response of the MULTIPLY Q BY meter. Test using an oscilloscope showed that the oscillator was running so it looked like a bad thermocouple. Figuring I had nothing to lose I removed the assembly and took it apart. I examined it, probed and poked at it, and put it back together. To my surprise it worked. I figured out a little later that the 0.04 ohm resistor was now more like 0.015 ohms. The detector tube was bad and I substituted a 6AV6 by using the base from the old tube to make an adapter so I didn't have to change the socket. I managed to get a rough Q calibration on it. At least I could measure the inductance of unknown coils.
Later I bought two Heathkit Q meters on eBay and even later two Boonton 260 Q meters. The two Heathkits arrived in working condition and I never had any major issues with them. The two Boontons were a different story.
Boonton 260 Repairs.
I have decided to make a long story short. I bought a Boonton 260 Q meter from someone on eBay and bands 2 and 3 on the oscillator were dead. I took the turret out but random factors did not operate in my favor. It came down to rewinding one of the coils. At that moment another 260 turned up on eBay at a reasonable price and I bought it. It had a higher serial number and the case was in much better shape. It was dead on bands 3 and 4. This time I was able to make repairs without doing any collateral damage. So I have a fairly good looking and fully functional and calibrated 260 Q meter. I will give you the benefit of my mistakes so you won't repeat them.
I assume you have bought a 260 from someone and the box has arrived on your doorstep. After you have opened the box, disposed of those annoying peanuts, and unraveled the puzzle of the bubble wrap, you are dying to plug it in. I urge you to resist the temptation. In spite of what claims were made by the seller I doubt if one in a thousand sellers knows how to operate a Q meter. Assume it hasn't been turned on for several decades and has been stored in an attic or basement for those intervening years.
Open it up and give it a thorough inspection before plugging it in and turning the switch. There are three screws on the bottom. If you overlook them you will find removing the cabinet a frustrating experience.
Removing the instrument from the cabinet.

Remove the three slotted screws on the bottom right side that are located about an inch and a half from the back.
The front/top portion of the case is held to the bottom/back/sides by 12 Phillips head screws. All of these screws are within half an inch of the edge of the panel. Remove them all.
Carefully separate the front and back. The chassis will rest on your bench and keep the front section from falling over.
There is a line voltage stabilizing transformer mounted on the back section. The cable from this connects to the chassis through a 4 prong Synch Jones connector. Unplug this connector by pulling upwards.
Now you may be able to separate the back from the front. I say may because it depends on whether someone has replaced the line cord with a three prong cord. Believe it or not the factory installed line cord had a two prong plug. The hole in the back panel would permit the plug to pass through. A three prong plug will not. Note: Units manufactured after the HP takeover used the old style HP oval detachable line cord.

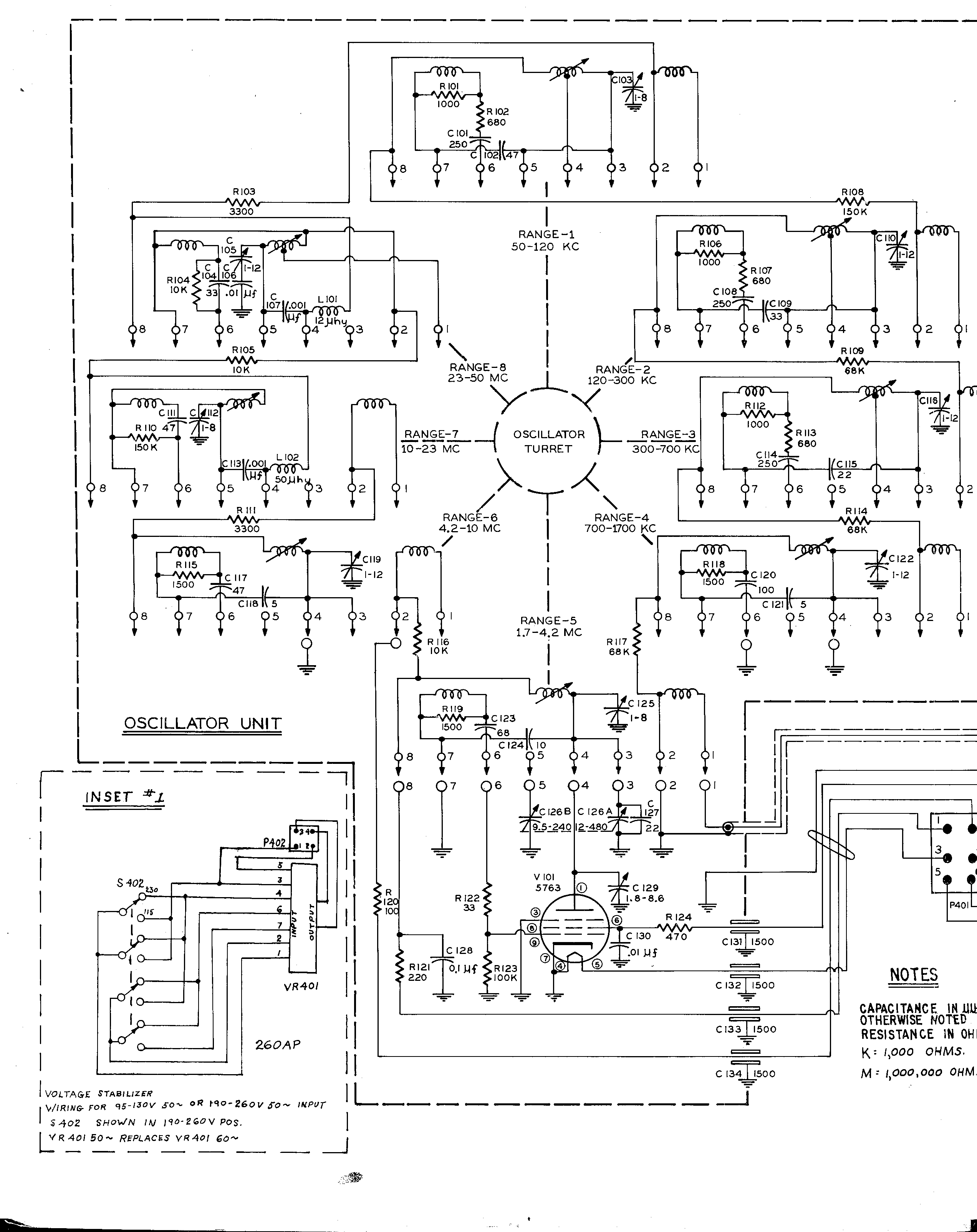
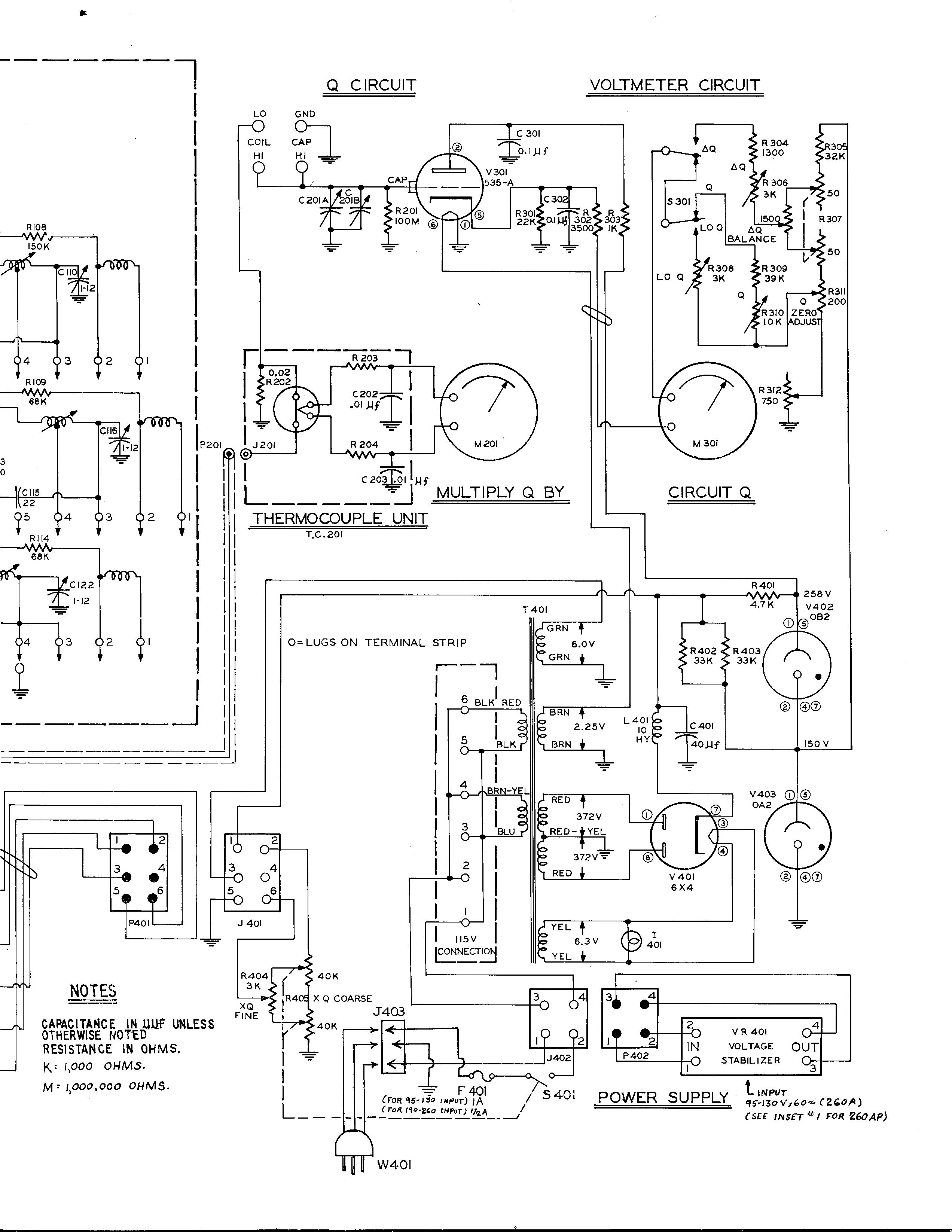
Schematic Diagram of Boonton 260 Q Meter.

For a verbal description click here
Be Forewarned, it is long and complex.

Inspection and Testing.

Now you have the 260 sitting on your bench with no way to fire it up. That's probably a good thing for the moment.
Inspect all of the tubes for breakage. Tubes have a coating of shiny metal on the inside that is usually over a small area near the top or bottom of the tube. This is one of the light metals that has the purpose of absorbing air molecules that linger in the tube. It is called the getter. If a white crystalline powder has replaced the metal it means the envelope is broken or cracked and air has entered the tube. Or as I sometimes say "The vacuum has leaked out".
Replace any tubes that show this abnormality.
Connect an ohmmeter to the filter capacitor, C401 in the schematic above. The reading should rise to several hundred k ohms.
Before performing the next test you need to remove the two voltage regulator tubes. Although they appear identical they are not. If it has not already been done write the tube numbers on the chassis with a pencil. Then remove the tubes and put them in a safe place where they will not be broken.
Connect your bench power supply to the filter capacitor observing polarity. If your supply does not have a current meter connect one in series with it. Set the meter to the 10 or 20 mA range.
Do not make heater connections. You do not want the tubes to be hot for this procedure.
Slowly advance the voltage of your power supply while watching the current meter. Note: DO NOT do this if your power supply is not adjustable. If it is not, study this page. You want the capacitor to show a small amount of leakage current. at its operating voltage of approximately 300 volts.
If the capacitor shows a short or a lot of leakage current and will not reform it must be replaced.
If the filter capacitor checks out or has been replaced you are ready to apply power. But first, take the line cord in your hands and flex it. If it feels stiff and makes crackling sounds DO NOT plug it in. Replace it.
Boonton did supply it with a two prong plug but they also installed a ground post on the back of the instrument. Aged electronics can develop shorts in places where you don't expect them, such as between the primary of the power transformer and the core. That will put line voltage on the instrument case and you could get a nasty shock or worse.
Unless the line cord is one of the HP detachable kind I recommend in the strongest terms that you replace it. Use the same strain relief. Don't forget to pass the end of the cord through the hole in the back section of the case before you permanently install it in the chassis. Unless you choose to butcher the case by enlarging the hole this will permanently tether the back and front sections of the case together.
Unscrew the power indicator jewel and check the lamp. If you have any doubt replace it with a number 47 or 51 lamp. Replace the jewel.
Remove the fuse cap and check the fuse. If it is missing or blown replace it with a 1 amp normal, not slow blow 3AG type.
To power it up you must bring the back and front close enough together for the cable from the line voltage stabilizer to reach. While working on mine in this configuration I received a tingle when touching both the back and front. The front is grounded to the safety ground through the chassis but the back is not. Use a clip lead to connect the two sections of the box together.
Now you are ready to plug and pray.
The power switch is on the XQ COARSE control in the same way as the off/on switch is on the volume control of a radio. Turn it on but do not advance the control beyond the click.
The power indicator did not come on.

The fuse is blown.
You must find the cause before trying power again. DO NOT WRAP THE FUSE IN ALUMINUM FOIL OR PUT IN AN OVERSIZED FUSE. DOING THAT MAY TURN A REPAIRABLE INSTRUMENT INTO A PILE OF JUNK.
The trouble is either the line stabilizer or the power transformer.
To eliminate the line stabilizer unplug its 4 prong plug. On the underside of the chassis temporarily tack solder short pieces of wire to connect pin 1 to pin 3 and pin 2 to pin 4.
Try the power again. If it comes on the line stabilizer is trash. It is potted with a tar like substance and can't be repaired. Remove it from the back of the cabinet and make the jumpers on the Synch Jones socket permanent. You should operate the instrument from an external line voltage stabilizer as described below.

The power indicator lighted but the fuse blew about 10 or 15 seconds after the power was turned on.

You skipped the filter capacitor test and reforming, didn't you.
Go back and do numbers 5 through 9 above.

The line stabilizer and filter capacitor have been eliminated as the cause. The fuse still blows as soon as the power is turned on. This doesn't look good for the power transformer.
If in your unit the transformer primary can be wired for 120 or 240 check the wiring to be sure it is correct for your part of the world.
Unplug all tubes. Don't overlook the oscillator tube which is in the oscillator section on the left side of the instrument.
Try it again.
If it still blows you are down to the last ditch. Unsolder all secondary wires from where ever they go.
Try another fuse. The indicator lamp won't come on even if the fuse does not blow. You unsoldered the wires to it, remember?
If the fuse does not blow there is a short most likely in the heater wiring.
If the fuse does blow the transformer is toast.
In case you are working without a manual I strongly recommend you get one. But if you can't find one here is the transformer data. It is also available in the schematic diagram above. The transformer has three heater windings and the standard center tapped plate winding. The plate winding is 372 - 372 at an estimated 75 mA. May also be listed as 744 CT. The heater for the voltmeter tube is listed as 2.25 volts. AES has transformers for antique radios that have 2.5 volt windings. You will have to get one of these and use a resistor to drop the � volt. This resistor will have to be found by cut and try. The other two windings are labeled 6.0 volts which powers the 5763 oscillator tube and 6.3 volts for the heater of the 6X4 rectifier tube. The schematic shows no connection to ground or B+ on the rectifier heater. The 6X4 is designed for the heater to be at ground potential. A single 6.3 volt heater winding can be used for both tubes. Check your Q meter to be sure there is no connection between the cathode and heater of the 6X4. The voltmeter tube current is probably no more than an amp and is likely considerably less. The heater current for the 6X4 is 600 mA and for the 5763 is 750 mA. Strangely the voltage for the 5763 heater is specified as 6.0 volts but with the added note +/- 10%. Both tubes could be operated from a single 6.3 volt winding. If you want to be particular you could use a resistor to drop the 0.3 volts but If I were the one doing it I wouldn't worry about it. There is plenty of room inside the cabinet to mount a new transformer however the original one has the cores horizontal. The transformer is right below the voltmeter and a vertical core might induce hum into the voltmeter. I recommend modifying the replacement transformer's shells so as to mount it with the core horizontal as in the original.
If all else fails log on to eBay and put a Boonton 260 Q meter on your wish list.

Further Testing.

Voltmeter Tests.
The voltmeter circuit in the Q meter uses an infinite impedance detector. The tube used bears the number 1659 which I had originally posted as 659. This mistake and others resulted in a very nice email from Pete who set the record straight. He writes.
"Max-
In your description of the BRC 160A and 260A "Q voltmeter tubes" you incorrectly called them 659's; they are actually RCA 1659's. These tubes are a ruggedized, high vacuum version of the 2A6 and have a very linear curve. A standard 2A6 will not work in a Q meter, nor will the 6 volt version, the 75.
BRC had two designations for these tubes: the 160A were stamped on the base, "535A", while the 260A tubes were marked 535B. During factory inspection of the incoming tubes, those that did not pass a particular test were then sold as replacements for the 160A tubes. Very few failed. The determining test was a Q measurement at 1MC using a 513A Q Standard. No one understood why, but 1MC test was the only point of failure with the tubes and Q could read 10-20 Q's low.
My qualifications for making these comments is that I was the lead production tech for the BRC product line and later as production supervisor and production engineer. Feel free to post this info in any way you may want.
Regards,
Pete"

If this tube is no good there is no point in going any farther with this particular instrument. Try to find another one and hope the 1659 is good.
Turn the instrument on and allow a few minutes for warm-up. Leave the COARSE MULTIPLY Q BY control set to minimum. Note: The name of the instrument is "Q METER". The upper meter on the instrument is also known as the "Q METER". Confused?

Connect a shorting wire between the COIL LO and HI terminals.
Rotate the Q ZERO ADJUST control over its full range.
You should be able to move the meter pointer above and below zero and adjust it to zero.
Press and hold the LOW Q lever. You should now be able to move the meter as high as 40 on the low Q scale. If you can't get it there don't fret. Making the pointer move is the important thing.
Lift the lever to the delta Q position. The meter should go to full scale. Release the lever.

If the meter did not move for any of these tests the news is not good. Before giving up do some basic tests around the tube. Make sure it is getting plate voltage. Test the meter movement to be sure it is good.

Set a digital ohmmeter to its highest resistance range. DO NOT DO THIS WITH A CONVENTIONAL VOM.
Clip the leads to the meter terminals. It might be a good idea to turn off the Q meter for this test.
The digital meter should read zero resistance. Turn the DMM to the next lower range while watching the Q meter. Continue turning the DMM to lower ranges. Eventually the Q meter will begin to deflect. If it does not, the meter is bad.
A new meter can be found but it will likely be a different size. Remove the meter scale plate from the old meter and put it in your scanner. Use a graphics program to make the image larger or smaller so it will be right for the new meter and print it out on photo paper. Glue the new scale inside the new meter.
If the meter checks good do this. There are 4 pots on the back of the chassis. Give each one a twist in both directions and then set it back to its approximate original position. Don't worry, we are going to end by calibrating the instrument. Check it again for meter response.
Check the network of resistors and pots in the meter circuit. If any are open replace them.
If all seems well with the meter connect an oscillator that can go at least to 50 kHz and 5 volts RMS output to the GND and CAP HI terminals. Set the output to 1 volt. The Q meter should read approximately 50. At 2 volts it should read approximately 100 and so on up to 5 volts where it should read 250. These readings depend on the calibration of the meter and you messed it up some when you exercised the pots. If all is well proceed to the oscillator tests.
If nothing you do will make the meter respond then the tube is most likely bad and replacements are even harder to find than hen's teeth. Save this instrument for spare parts and buy another one.
Oscillator Tests.
Assuming you got through that without finding anything wrong or you have been able to make repairs there is more to come. I assume you have the 260 turned on with the indicator lamp illuminated.

Set the band switch to the lowest band as indicated by the yellow arrows in the dial scale window.
Set the frequency to 50 kc (kilohertz).
Cautiously advance the XQ COARSE control while watching the MULTIPLY Q BY meter.
The meter should begin to read up scale. Note how there is a time lag between movement of the control and changes in the meter reading.
Turn the XQ COARSE control back to minimum without turning the instrument off.
Change to the next band and advance the XQ COARSE control. Again you should see a deflection of the meter pointer.
Repeat steps 3 through 6 for all 8 bands. If you did not have a meter deflection on any band make a note of it and continue testing.
Set the frequency dial to 75 kc and run checks 3 through 6 on all 8 bands. Note any dead bands.
Set the frequency dial to 120 kc and repeat steps 3 through 6 for all 8 bands.

If you obtained a meter deflection on all 24 tests above go out and buy a lottery ticket. You are a lucky individual. If you saw deflection on 1 or 2 of the frequencies on one band go back and check that band again at low end, middle, and high end frequencies. If operation seems intermittent rotate the band switch back and forth across the troublesome band.
Operation of the oscillator over only part of a band is likely an indicator of a weak 5763 tube. Replace it with a newly purchased tube. The highest probability event is for deadness on all of one or more bands. You have no choice but to take the oscillator apart and repair it.
Repairing the Oscillator Coils.

Unplug the power cord and the Synch Jones plug to the line stabilizer.
Set the back portion of the cabinet on the floor or out of your way on your bench.
Remove all three knobs from the oscillator section on the left.
Unplug the 6 pin Synch Jones plug from its socket on the chassis.
Disconnect the coaxial cable from the thermocouple unit.
Remove the 6 large Phillips head screws that hold the oscillator section to the panel.
Set the front and back sections of the cabinet on the floor out of your way. You are going to need lots of workbench space for this.
Now you will see the gears that drive the dial mask. No cheap plastic gears for Boonton, this instrument was made to last.
There is nothing to hold the dial mask in place so remove it before it falls off. Use a pencil to mark "back" on the back (unseen) side of the mask.
Remove the top and bottom covers of the oscillator unit.
Now you will see the turret.
When I took both of mine apart I removed the little "C" retainer that holds the large solid gear on its shaft. This was a mistake because I lost the retainer three times. Fortunately my wife was able to find it for me. The retainer looks like there is a special tool for removing and installing it. I had thought of making one but it didn't get past that point.
I am going to recommend a different procedure which does not require removing this gear.
There is a spring clip that makes good electrical contact with the bottom cover plate. It is in just the right place and has the right shape to allow the detent roller to be lifted from the turret and hooked over the clip. Do this. The turret will now be easy to turn.
Note: I'm not providing pictures for two reasons. 1) You have the instrument right in front of you. 2) I didn't take any while I had the oscillator apart.
The plates that make up the ends of the turret have bushings on them. The rear plate has its bushing outside of the turret. Locate and loosen the two Allen head screws that hold it to the shaft.
The front plate of the turret has its bushing on the inside. The screws are not in the same places as on the rear bushing. Locate and loosen them. The turret should now rotate freely independently of the shaft. Do not let the prongs engage the contacts. They are no longer in alignment and could damage them.
Loosen the screws that hold the gear with spokes at the front of the unit. Theoretically the shaft should slide freely out of the back of the oscillator unit. Right!
At this point you will find it helpful to apply a SMALL amount of 3 in 1 oil to the shaft. Do not pour it on. Place a drop of oil on your finger tip and apply it to the shaft. Do not lose patients and start applying force. You could do irreparable damage by doing that. Work the turret and gear gently back and forth until the shaft comes out.
Now you have the turret in your hand.

The first thing you will notice is that there are only 4 coil forms. There are two bands worth of coils on each form. Bands 8 and 1 share a single coil form. Then bands 2 and 3, bands 4 and 5, and bands 6 and 7. On the back of the turret are stamped markings with band numbers and the letters F and B meaning front and back. The back is the plate with the adjustable piston capacitors on it. Referring to the schematic make continuity tests on the coils of the band or bands that is/are dead. Pins 1 and 2 are closer to each other than all the others. In all likelihood you will find one of the coils on the nonworking band to be open.
If all coils are intact check the resistor that connects between pin 8 of the nonfunctional band and pin 2 of the next higher band. The purpose of these resistors is to approximately equalize oscillator output between bands.
If one of the coils is open you have to partially disassemble the turret. The front plate does not have any components mounted on it.
>li>The position of the front plate relative to the back plate is important. This is because of access to the setscrews that hold the front plate to the shaft. Mark the front plate so you can get it back in the same position as it originally was.
The front plate is fastened to the phenolic frames by 8 screws, two in each frame. These are machine screws with nuts and lock washers. Remove each screw while catching the nut and lock washer on your fingertip. Lift off the front plate.
Now you can see into the turret. Inspect the points where the wires from the open coil connect to the contact pins. Most likely one will be open. If you have a keen eye and a steady hand you may be able to work on the turret without any further disassembly. I had to remove the coil and phenolic frame assembly from the back plate to work on it.

There are resistors on both sides of the phenolic frame. There is also one in the middle which does not have to be unsoldered. Unsolder each resistor where it connects to pin 8. There are piston capacitors that are soldered to pin 3 on one side and 4 on the other. Unsolder them both.
Remove the two screws with nuts and lock washers that hold the phenolic frame to the back plate.
You now have the coil form and phenolic frame in your hand.

Here is where you can benefit from my mistakes. The fine wires from the coils run in heavy sleeving, compared to the wire size, from the coil to the contact pin. I tried to stretch the wire and solder it back to the pin. It worked the first time but the second time the wire broke off where it entered the coil. If it had been on the outside of the coil I could have sacrificed one turn to get some wire to solder to. That didn't happen.
Solder a short length of number 22 or 24 insulated wire to the pin. Shorten up the sleeving and solder the fine wire from the coil to the end of the solid wire. The insulation on the coil wire is of the type which melts at soldering temperatures.
Be sure the exposed solder joint is not positioned where it can short out to other pins or wires.
Perform the continuity checks again. If it checks out put everything back together.
When reinstalling the turret in the oscillator be careful not to damage the spring contacts that make connection to the pins.
After you have the shaft back in place tighten the screws on the gear to prevent front to back movement of the shaft.
Align the pins with the spring contacts and gently rotate the turret to bring the pins between the contacts while one of the Allen setscrews is accessible.
Rotate the turret slightly while holding the shaft. This will help the pins to align themselves between the spring contacts.
When you are sure the pins are properly aligned tighten the accessible Allen setscrew. Then tighten the three remaining screws.

Release the detent roller from the spring clip where you placed it a long time ago.
Do not put the shield covers on until you have tested the oscillator.
Do not install the dial mask just yet.
Temporarily mount the oscillator unit to the front panel with two screws placed on a diagonal.
Install enough knobs to enable you to change bands and tune the frequency dial.
Reconnect the coaxial cable to the thermocouple unit and the Synch Jones plug to the socket on the chassis
Plug in the Q meter and perform the oscillator checks again.
The oscillator is now working properly. Right?

Reinstalling the Dial Scale Mask.

Turn off the Q meter, disconnect the 6 pin Synch Jones plug, disconnect the coaxial cable, and remove the oscillator from the front panel.
Turn the oscillator around so you can see the rear of the turret through the access holes. You should also be able to see the band numbers.
Set the band switch to band 1, 50 kc to 120 kc.
Slide the dial scale mask over the shaft in the center of the dial scale disc.
Rotate the mask until the innermost opening is centered above the shaft. Engage the teeth on the outer perimeter of the mask with the solid gear.
Temporarily mount the oscillator unit to the front panel with two screws.
Rotate the band switch to check the alignment of the scale mask.
If it is not right make notes on how far and which way it is off. Remove the oscillator from the panel.
Slide the bushing of the mask forward and move one or more teeth on the mask gear past the teeth of the solid gear.
Push the mask back into position.
Mount the oscillator to the panel.
Repeat steps 8 through 11 until the mask is positioned properly. As shown below.

Before buttoning it up lets verify that the mask is set correctly.
Plug in the 6 pin Synch Jones plug and connect the coaxial connector.
Turn on the Q meter and set the frequency to 50 kHz.
Connect short pieces of hookup wire to the "GND" and "LO" terminals on top of the Q meter.
Adjust the COARSE and FINE MULTIPLY Q BY controls for a reading of 1 on the MULTIPLY Q BY meter.
Connect your oscilloscope to the GND and LO terminals.
Read the frequency by measuring the period of the wave. Note: The voltage level at these terminals is too low to trigger most frequency counters.
If all is well reinstall all of the shield plates on the oscillator unit and all of its mounting screws.

Congratulations. You now have a fully functional Boonton 260 Q meter.
Heath Q Meter Repairs.
The Heath Q meter employs much simpler electronics and mechanics and is much easier to work on than the Boonton. All the same you should do an internal inspection before firing it up.
Removing the Instrument from its Cabinet.

There are two sheet metal screws on the back which hold the chassis to the back half of the cabinet. Remove them.
There are 5 sheet metal screws on top of the instrument. Remove them.
There are two sheet metal screws on the front of the instrument. Remove them. Do not remove any screws that are farther than 1/4 inch from the edge of the panel.
Lift the panel slightly and move it forward. Snake the cord through the hole in the back of the cabinet. The plug will pass through the hole unless someone has replaced it with a 3 wire cord and plug.

Now an inspection is in order.

Inspect all tubes to be sure their getters are shiny.
Examine all resistors to make sure none of them are charred from being overheated.
Inspect the filter capacitor under the chassis to make sure it is not bulging or has not exuded any material. If it has, replace it.
Unscrew the green lamp cover and remove the indicator lamp. If there is any doubt about its integrity, replace it with a number 47 or 51 lamp. Replace the green cover.

Replacing the filter capacitor, C14A and C14B.
Even if you find the capacitor to be good you may be inclined to replace it. This is not a bad thing but don't overdo it. Larger values are readily available now as compared to when the instrument was made but just because you can doesn't mean you should. Don't replace with anything larger than 22 u f. Larger capacitors will place increased stress on the rectifier tube and shorten its life.
Another thought which is likely to cross your mind is to replace the rectifier tube with silicon diodes. DON'T DO IT! Silicon diodes will add more than 50 volts to the B+ voltage. This will place increased stress on R14, R15, R17, and V4. Not only that but the values of +80 and -70 volt supplies will be thrown off and the RF voltmeter may not work at all.
This instrument has no fuse. You might want to think about adding one. The first power on should be done in slightly subdued lighting. If your bench is very brightly lighted as mine is turn off some of the lights. Because of the wiring of a jumper in the Voltage Regulator tube, 0D3, VR150, the instrument will not be powered if this tube is removed from its socket. This is the large tube to the left of the power transformer as viewed from the back of the instrument.
Initial Power Up.

Plug in the line cord and turn on the power switch by rotating the SET LEVEL knob clockwise. You will feel and hear the click. The green indicator lamp will come on.
Turn the instrument around and watch as the tubes warm up. You should see an orange glow in most of the tubes. The 0D3 VR150 should glow purple.
Use your nose. If you smell anything burning unplug the power cord immediately.
The orange glow of the heaters may be hard to see in some of the small tubes. If everything is going well turn the Q meter around so you can see the meter and operate the front panel controls.
Operational Tests.

Connect a shorting wire between the two coil terminals.
Set the CAL "Q" switch to "Q". Rotate the SET ZERO control. You should be able to move the meter up and down and set it to zero. If the meter will not move at all proceed to the next steps.
Change the CAL "Q" switch to the CAL position.
Turn the SET LEVEL control clockwise. You should be able to bring the pointer above the multiply Q by 1 mark (X1). There should be enough reserve in the control to bring the pointer somewhat beyond this mark. If the meter does not move in this step proceed to "Power Supply Checks.
Check the above on all four bands A, B, C, and D, and at frequencies near each end and the center of the tuning range.
If everything works you're in luck. Proceed to Heath Q meter under Calibration.
If you need to troubleshoot your Heath Q meter here is a schematic diagram.

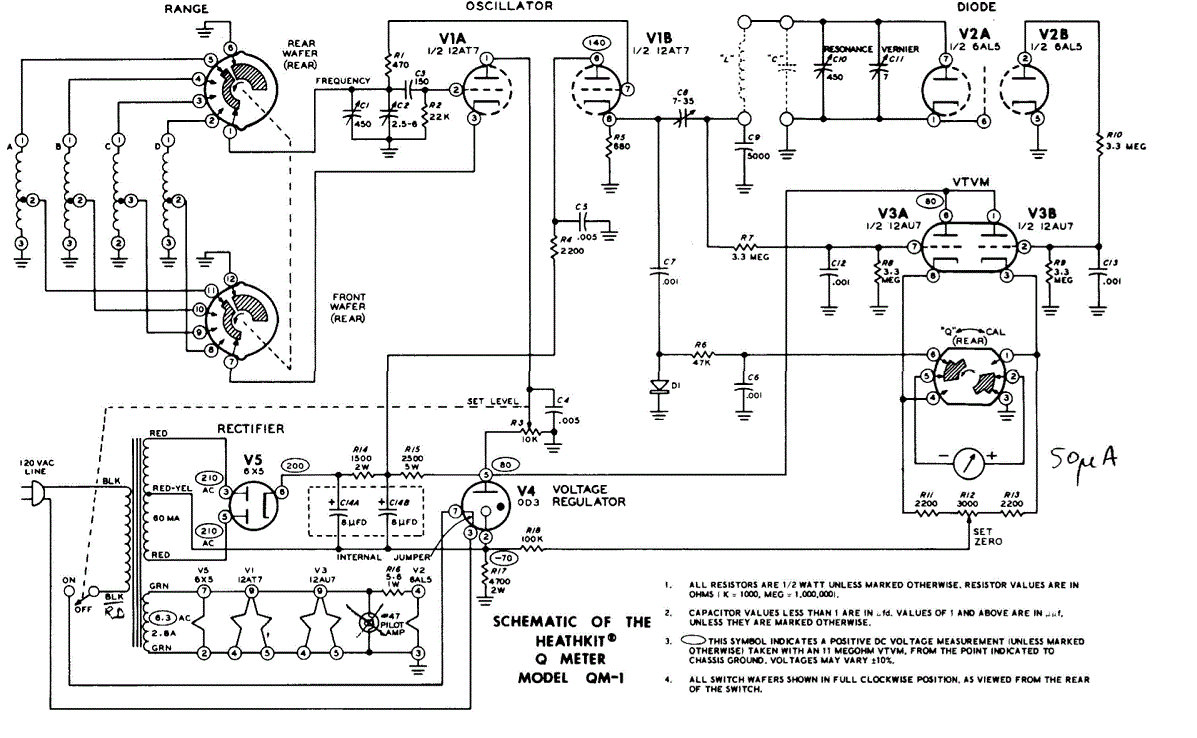
Schematic Diagram of Heath QM-1 Q Meter.

For a verbal description click here

Power Supply Checks.

Make sure the heater in V5, 6X5, is lighting up orange.
Measure the voltage at the cathode, pin 6, of V5. If it is very much below the specified 200 volts, set your test meter to AC. If you read 100 volts or more C14A and C14B will have to be replaced. If there is little or no AC but also not much DC the tube V5 may be bad. Replacement with silicon diodes is not recommended. Obtain the original tube type.
Check the DC voltages at pins 2 and 5 of V4. If they are far off check R14, R15, and R17.
Voltage Regulator tubes rarely fail at all but when they do they fail in a pretty much binary way. The tube will either glow purple and be good or not glow and not function.
If the power supply isn't working there is no use in continuing to test the instrument. The power supply is mama and if mama aint happy aint nobody happy.
If the power supply is functioning chances are you will see meter deflection on either Q or Cal.
If you get deflection when set to Q but none on Cal you must look to the oscillator. It means that the oscillator is not running.
If the instrument has been stored in difficult conditions such as in an attic or basement the switch contacts may be so corroded as to prevent oscillation. Try a good cleaning with contact cleaner.
If you can get meter deflection on some bands but not on others check the coils for continuity. If there is continuity, keep cleaning.
It may come down to replacing the 12AT7.
If tests with an oscilloscope or radio receiver tell you that the oscillator is running but there is no meter deflection check D1. When this instrument was made D1 would most likely have been a 1N34A. I don't think it would make a lot of difference if you replaced it with a 1N4148 silicon diode. Don't use a rectifier diode such as a 1N4007 or similar.
If one or more of the oscillator coils is open or otherwise damaged you are out of luck. Your only hope for repair parts is to find another QM-1 on eBay.
If you get meter deflection on cal but none on Q check resistors R11, R12, R13, and R18. Also check the voltages. If resistors check good the 12AU7 may need to be replaced.
Calibration.

Boonton Q Meter.

Read this even if you have a manual.

Frequency Calibration.
There is a small variable capacitor accessible on the back of the oscillator module that will allow adjustment of the high end of all bands. If one or more bands are out of calibration at the low end you are probably out of luck. Pete informs us that,
"Unfortunately the 260A oscillator coil slugs were glued in place with "Glyptol" or "Ambroid" or "Q-Max". All are nearly impossible to dissolve after 60 years. The slugs in the range 7 and 8 were different from the others and painted blue.
Pete "

Q calibration.
The calibration procedure given in the 260 manual depends on the voltage across the 0.02 ohm resistor being 20 millivolts when the MULTIPLY Q BY meter is set to 1. Abuse by a previous owner, swapping of thermocouple units from another Q meter, or the passage of time, has very likely caused the voltage to be off from this ideal value.
The manual discusses ordering a replacement thermocouple unit. It states that the serial number must be provided with the order because the thermocouple unit had to be match to the resistance of the MULTIPLY Q BY meter movement. I assume that when Boonton ordered a lot of meters they could specify matching of the resistances of the whole lot but not the specific resistance. The next lot to be ordered might have a different resistance. The thermocouples have to match the meter resistance.
To check the voltage you need a meter capable of accurately reading 20 mV at a frequency of at least 1 MHz. An HP 400 D or later version is perfect for this. I used the voltmeter feature of my HP 334 A distortion analyzer. Failing any of these an oscilloscope will do if you can verify its calibration. Remember that 20 mV RMS is 56.57 mV P-P.

Set the oscillator frequency to the one you are likely to use the most for example 455 kHz.
Connect your measuring device between the GND and COIL LO terminals. It may be necessary to use short lengths of hookup wire. Small clips will not hold reliably on the Q meter terminals.
Set the meter or scope to the appropriate range.
Advance the MULTIPLY Q BY controls until you have a reading of exactly 1 on the MULTIPLY Q BY meter.
Measure the voltage. If it is within 1 % of 20 mV leave it alone and buy another lottery ticket. Otherwise proceed to "Voltage is low" or "voltage is high" sections below.
In the section below you are going to determine how much resistance to connect either in parallel with the resistors that are mounted to the thermocouple unit or in parallel with the meter movement to bring the MULTIPLY Q BY meter into calibration. If you happen to have a decade resistance box your job will be as easy as it can be. Heathkit made a model back in the day. There are quite a few General Radio and Leads and Northrop models on eBay however Their accuracy may be in considerable question.
A resistor substitution box might get you close but they have large steps and the accuracy is not good unless you have replaced the resistors with modern carbon film 5% resistors.
About the same amount of work involves using a low resistance pot. Set it to obtain the desired results, disconnect it from the circuit and measure its resistance with a DMM.
If it comes down to it soldering and unsoldering resistors is possible but not very much fun.
Voltage is Low.

With your test meter connected to read the voltage across the 0.02 ohm resistor set the MULTIPLY Q BY COARSE and FINE controls for a reading of 20 millivolts. Don't worry about the meter being off scale. Meters are designed to withstand a steady state current of at least and usually more than 2 times full scale current. What damages a meter is the mechanical shock of being slammed against the stop. If it is put on the stop by a gradual increase in current no damage will result.
Connect your test resistor, whatever it is, across the terminals of the MULTIPLY Q BY meter.
Adjust the resistance until the meter reads 1 or as close as you can get. You may have to end up connecting some resistors in parallel to get the resistance you need. For example a 4.7 k ohm resistor in parallel with a 220 ohm resistor to get a resistance between 200 and 220 ohms.
Install the final resistor or combination of resistors permanently. Soldering is recommended. If you have some lugs that will fit over the meter bolts you can solder your resistors to them and put them under the nuts that hold the lugs that were installed by Boonton. If you don't have such lugs then solder the resistors to the lugs that are already on the meter bolts.
Check the voltage again to be sure it is 20 mV when the MULTIPLY Q BY meter reads 1.

Voltage is High.

Turn off the instrument and unplug it.
In the following 2 steps you will remove the voltmeter tube. This tube is literally irreplaceable. Treat it like it's made of solid gold. It's probably worth even more than that
Removing the grid cap connection from a tube is one of the most common ways in which a tube is damaged. What happens is that the glue holding the cap to the glass fails and the cap comes off breaking the wire which makes contact between the grid inside the tube and the top cap. Do not just give it a yank. Gently try to move it either by pulling or twisting. If it doesn't seem to want to budge stop right there. Look carefully at the cap and its connector. Usually there is a gap between the top of the cap and the inside top of the cap connector. Insert a small screwdriver into this gap and gently pry by rotating the screwdriver. Take actions that will place a minimum of force on the cap relative to the envelope.
To unplug the tube don't grab the glass envelope and start pulling. Grasp it by the Bakelite base and gently work it out of the socket. If it is stubborn a bit of prying with a screwdriver between the base and the chassis will help.
Now that you have the tube out don't leave it on your bench where it can roll off and break. Put it in a safe place.
While the instrument is off check the mechanical zero adjustment of the meters. You might as well adjust both of them while you have the opportunity.
Turn the instrument on and after a warm-up period set the MULTIPLY Q BY COARSE and FINE controls for a reading of 1 on the MULTIPLY Q BY meter.
Connect your AC voltmeter to the terminals that are marked GND and COIL LO.
Adjust the controls for a reading on your meter of 20 mV.
There are two resistors, R 203 and R204, soldered to terminal strips on the thermocouple unit. These resistors need to be decreased in value by having other resistors connected in parallel with them. This is pretty much a trial and error process.
Connect resistors in parallel with each of the two resistors. Try to keep them close to the same value. Adjust their values until the meter reads 1 when the output voltage is 20 mV.
Put everything back together.

If you have a manual proceed to "Adjustment and Calibration" on page 17. If you have no manual continue on with this page.
There are 4 adjustment pots on the back of the chassis. Use a pencil to mark them on the chassis as follows. Left to right as viewed from the back of the instrument. R312, R308, R310, and R306.
Voltmeter Calibration.

Turn off the power to the Q meter and check the mechanical zero adjustment of the Q meter.
Turn on the power but don't advance the XQ COARSE control. Turn the XQ FINE control fully counter clockwise. If the Q meter is not warm from being previously operated allow 15 minutes for warm-up.
Connect a shorting wire between the GND and either HI terminal.
Set the Q ZERO control to the middle of its rotation.
Adjust R312 to bring the pointer of the Q meter as close to zero as possible.
Press the LO Q lever down and adjust the Q ZERO control for an indication of exactly zero on the Q meter.
For the following procedure you need an audio signal generator or function generator that has a maximum frequency of at least 50 kHz but 1 MHz is much to be preferred, and a maximum output of 5 volts RMS when the sine function is selected.
Remove the shorting wire and set the capacitance dial to minimum.
Connect the signal generator to the GND and either HI terminal. Set its frequency to the same frequency you used when calibrating the 20 mV signal.
Connect an AC voltmeter that will measure RMS voltage to an accuracy of +/- 2% at the frequency being used to calibrate the instrument.
When the applied voltage is 1 volt the meter should indicate 50, 2 volts = 100, 3 V = 150, 4 V = 200, and 5 V = 250. Find the best compromise setting of R310 to obtain these readings.
In actual practice I have rarely seen a coil with a Q higher than 100. If there is no good compromise, adjust R310 for best accuracy between 50 and 100. If you find that your work involves higher Q coils you can always go back and change this calibration later.
When the LOW Q lever is pressed down the voltages and Q readings are as follows. Note: Be sure to read the low Q scale on the meter. 1.2 V = 60, 1.0 V = 50, 0.8 V = 40, 0.6 V = 30, 0.4 V = 20, and 0.2 V = 20.
Adjust R308 for the best compromise. If one can't be found I recommend best calibration around 30 to 40.
Set the generator to 3.0 volts output.
Lift the lever switch to the delta Q position. Adjust the delta Q COARSE and FINE controls for a reading of 50 on the delta Q scale which is red. Note that this is a backward scale, that is 50 is at the left and zero is at the right. You may release the lever switch.
Change the signal generator output to 4.0 volts.
Lift the lever switch and adjust R306 for a reading of zero on the red scale.

This completes calibration of your Q meter. Put the cabinet back together and enjoy.
The Heath Q Meter.
There is only one way to calibrate the Heath Q meter. You must have a coil that has a known Q. If you know someone who has a Boonton Q meter you may be able to get them to calibrate a coil for you. Take them, or send them, a 1 mh or 2.5 mh RF choke and have them read it for you. Have them read the Q at 250 and 455 kHz to give you two points of calibration. Be sure to ask them to position the coil a little above the metal top of the instrument as shown in the picture below.

When you connect the choke to your Q meter be sure to do the same. Note: You need to have the Q meter out of its cabinet to perform this procedure. The trimmer capacitor you have to adjust has a metallic screw that needs a metallic tipped alignment tool to turn. That is as opposed to a plastic tipped tool. The tool you need has a plastic shaft and a small metal tip for turning the adjustment screw. There is no particular danger in using a regular metal screwdriver but the reading will be altered by contact with the screwdriver. You will have to make a small adjustment, take the screwdriver away and read the meter. Then repeat if the reading is not correct.

Turn the Q meter around and locate the calibration capacitor. As viewed from the back of the meter it is just above and a little to the left of the voltage regulator tube. It is mounted to a partition with a hole to allow access to the adjustment screw. Position your alignment tool and turn the screw a little to get the feel of it.
Now turn the Q meter back around for access to the front.
Connect your calibration coil to the COIL terminals.
Turn on the power and allow a few minutes for warm-up.
Set the oscillator to the frequency at which your coil was calibrated.
Change the CAL "Q" switch to the CAL position and adjust the pointer over the X1 mark.
Change the CAL "Q" switch back to the "Q" position.
Make sure the capacitance/inductance dial is not set near the peak.
Adjust the SET ZERO control for zero on the meter.
Tune the capacitance/inductance dial for a peak. Use the VERNIER dial to get it right on the peak.
Now get your alignment tool into the screw on the calibration trimmer.
Adjust the trimmer until the meter reads the Q value of the calibration coil.
recheck the zero adjust and peak reading by repeating steps 5 through 12.
Set the oscillator frequency to the other frequency at which your coil was calibrated and repeat steps 6 through 12.
You may have to find a compromise setting of the trimmer to give best readings at both frequencies.
The Line Voltage Stabilizer.
I had two line voltage stabilizers blow out on two successive nights. I was doing a project in which I would make a series of measurements and then leave the Q meter unused for a long period of time. I left it on and the stabilizers grew quite warm, I may say even hot. The first one to go out made a slurping sound and the red indicator went dark. Upon removal from the cabinet I found the thing had spewed out a thick black substance. I cleaned it up as best as I could and replaced the stabilizer with the one from the other Q meter.
The second one didn't make a sound. When I wanted to make another measurement I found the meter reading zero and the red light was out. Maybe if I had run the Q meter in short bursts with cool-off times between I might still have the original stabilizer plus a spare. I suspect this procedure would have only put off the inevitable for a short time. 50 year old electrics are going to fail and that's all there is to it.
Repairing the original stabilizer.
I really didn't want to get into the mess of melting out the potting tar from the line voltage stabilizer and making repairs but it is possible. I know that because I have heard from Bob W6DDX who has done it. I post the information with the hope that it may benefit someone else.
"However you stated that the constant voltage regulator is not repairable. I disagree. One of my Q meters had a failure and I was about to give up. I bypassed the regulator and all worked well until I got a tingle when touching the panel. On further investigation I discovered that the regulator also offered line isolation and wasn't so easily dispensed with.
I bit the bullet and created a genuine mess by disassembling the tar potted capacitor. I obtained some ac capacitors of the correct value when put in parallel and stuffed them into the can. Now all is well. I have the line regulator in perfect operation and my chassis is isolated. No need for an external isolation transformer."

Replacing the Stabilizer.
I was not able to find a replacement stabilizer that would fit into the cabinet of the Q meter. The only alternative was to mount it on my bench and remember to plug the 260 into it instead of the unregulated line. My rationalization for this is that I will probably never have an occasion to use the meter away from my bench.
Someone found a suitable regulator for me on eBay and I bought it. It could probably be purchased through another source such as Mouser, Allied, or DigiKey. Maybe even Amazon. It is a General Electric Model 9T91B4130. It's rating is 120 VA which makes it just right for the 260 which is fused with a 1 amp fuse. Here is a picture of how I mounted it to my workbench.

It is too big to fit inside the case of the 260 so I mounted it on the back wall of my workbench. It does not come with any sort of plugs or outlets. I bought a plug strip at the home center and cut its cable. I knocked out the knockouts on the stabilizer and installed Romex connectors. I don't know why they are called connectors. They are actually clamps. I mounted them with the nut on the outside and the clamp on the inside. I cut the plug strip cable to the length I wanted and fed it into the Romex connectors and connected the wires with wire nuts. It means that I can't use the 260 away from my bench but why would I want to do that anyway.
Useful Accessories.

The work coil set is one that I have known about for many years. Although I mention rolling your own I doubt if this is practical. Mine came with my first 260. The instrument is now nothing but a parts donor but the coil set was worth the price of the Q meter.

The other accessory that came with that first Q meter is a transformer that will match a 500 ohm load to 0.3 ohms. In case those numbers don't ring a bell, 500 ohms is the approximate output impedance of most commonly used audio generators available in 1955 and 0.3 ohms is the input impedance of the thermocouple module. If that still doesn't do it for you the frequency range is listed as 1 kc to 50 kc. Something else that was true in 1955 was the generators had a lot more output. The most I can get out of my digital function generator is 7.07 volts RMS. Most tube era generators would output as much as 20 or 25 volts.
This matching transformer will permit an audio signal generator to be substituted for the oscillator in the 260. So if an audio generator were to be used the inductance chart would have the following additions.

INDUCTANCE FREQUENCY
0.1 - 1 h 25 kc
1.0 - 10 h 7.9 kc
10 - 100 h 2.5 kc

My attempts to measure two iron core inductors met with utter failure. One measured about 5 henrys on a digital RLC meter and the other measured about 0.5 henrys. I was able to find a peak with a toroidal inductor that was marked 17 henrys and measured 17.5 on the RLC meter. It read 30 h with a Q of 50 on the 260 with the external oscillator at 2.5 kHz. As we learned above this indicates a large distributed capacitance. One more try. The primary inductance of a Hammond 1645 output transformer. The digital read 25.6 h with a Q of 3.66 at 1 kHz. But on the 260 there was no peak to be found. I guess this accessory is not as useful as I thought it might be.
That's About all I can think of to say.
If you have unanswered question(s) be sure to drop me an email with it or them. Not only will I answer them in a return message I will most likely post the answer here.

Home

Or use your "Back" button to return to where you were.

This page last updated July 30, 2014.

INDUCTANCE	FREQUENCY
0.1 - 1 h	25 kc
1.0 - 10 h	7.9 kc
10 - 100 h	2.5 kc