
Figure 1
Building an IF (intermediate frequency) amplifier is not a totally trivial matter. Tube selection is no big deal as there are only a few viable choices. The problem is the double tuned transformers that make up the coupling between stages. And there are other coupling methods that can be used.Typical IF Amplifier.

Figure 1
I must admit that this is more typical of a general coverage single conversion receiver than a more sophisticated one. However, it is a place to start. The double tuned transformers may be replaced by single tuned coils and there may be a crystal or mechanical filter somewhere in the IF strip. When such a filter is used it sets the bandwidth and the tuned circuits are just for providing a high impedance in the plate circuit of tubes so they will have higher gain than can be obtained with a resistor or non-resonant RF choke.
B+ and AGC decoupling are absolutely necessary to prevent oscillation. For a VLF IF the capacitors may need to be increased in value but be careful. Too much filtering in the AGC can render it unstable. That is, it will overshoot or over correct, then over correct in the opposite direction, and so on. Because the strength of signals in the HF band is constantly changing such an AGC will never settle down to a stable point.
Coupled Tuned Circuits, Just a Little Theory.
If you have ever taken apart an old style IF transformer from an early AA5 radio you may have been astounded as I was when I did it.

Figure 2
I wondered how they could couple any signal with the coils so far apart. At that time I knew nothing about critical coupling. As you move the two coils closer together the coupling is increased and farther apart coupling is decreased. So shouldn't they be as close together as physically possible? The graph below of a simulation shows what happens as coupling is increased.

Figure 3
The double humped curve is an over coupled state, the tallest single humped curve is critical coupling and the single humped one that is not as tall is an under coupled condition. Obviously the critically coupled condition is the most desirable. As the two coils are moved closer together the two humps become farther apart and the valley between them becomes deeper. This is undesirable in most circumstances. If a wide response is needed a double humped transformer can be used together with a single humped one to fill in the valley which will make a wider overall curve than could be obtained with two identical transformers.
But what makes that valley in the middle of the response curve? Let's look at the phase relationships in two coupled coils.
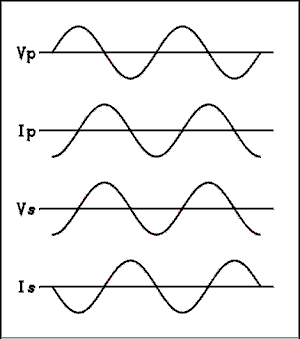
Figure 4
Because the coil is inductive the current will lag the voltage by 90 degrees. So the figure shows Vp the primary voltage 90 degrees ahead of Ip the primary current. The voltage induced in the secondary Vs is in phase with the primary current. The secondary current is 90 degrees behind that so the secondary current is 180 degrees out of phase with the primary voltage.
This induction business goes both ways so the secondary current will induce a voltage back into the primary which is 180 degrees out of phase with the applied voltage. This will cancel the applied voltage so there won't be any primary current to induce a voltage in the secondary. That means that there won't be any current in the secondary to induce a canceling voltage back into the primary so there will be a voltage again. But when there is voltage on the primary there is primary current which will induce a voltage in the secondary which will…
Obviously complete cancelation can't happen but an equilibrium is established where in the effective primary voltage is reduced. This accounts for the dip in response which appears at resonance. Slightly off resonance the phase relationships change and the cancelation is less than at resonance. This is shown in the simulation in figure 5.
But wait, there is more. When an LC circuit is driven at its resonant frequency the current in the inductor and capacitor is much larger than the current being supplied by the generator. How much more? Q. The current that is going round and round in the tuned circuit is Q times the supply line current. The current in the inductor and capacitor is called the circulating current or sometimes the tank current. This large current causes the induced voltage to be much larger than it would be if there was no resonant condition. The critical coupling factor K is,
K = 1 / sqrt(Q1 Q2) Where Q1 and Q2 are the Q values of the two coils respectively.
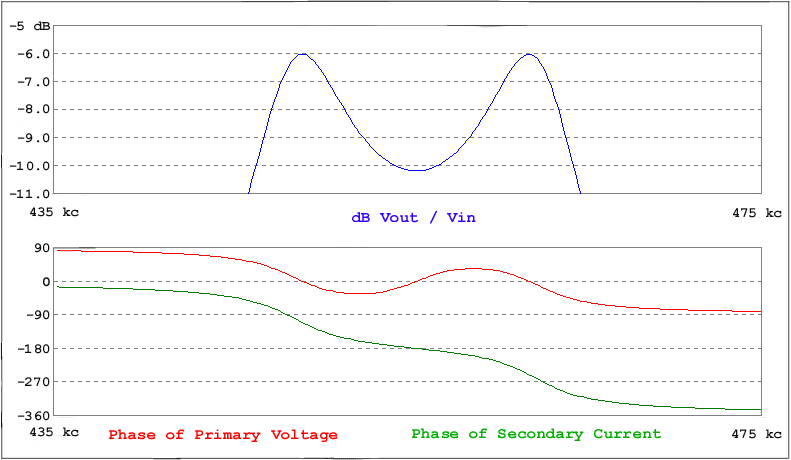
Figure 5
In figure 5 two over coupled resonant circuits are simulated. In addition to the amplitude response the phase of primary voltage and secondary current are plotted. Note that at the resonant frequency the phase relationship is 180 degrees and moves off of that value away from resonance.

Figure 6
Figure 6 shows that this is not all theoretical simulations. This sweep was taken on a transformer built with 1.2 mH coils as shown farther down this page. The reason the two peaks are of different heights is because both tuned circuits were not tuned to exactly the same frequency. The scale is 10 kHz per division with 455 kHz in the center. The vertical scale is linear and is simply 100% at maximum.
A circuit that uses capacitive coupling instead of magnetic will be shown even farther down this page. It operates the same way, producing a double humped response if it is over coupled.
Making Double Tuned Transformers.
I once had a page elsewhere on this site giving detailed instructions for making a set of 455 kHz IF transformers for use in home brewed AM radios. But like a manufacture I had supplier problems. One went out of business and the other discontinued the parts I had specified. I'm going to reconstruct the page with the caveat that you are on your own when finding the parts. I can and will give you a link to the aluminum box. If the link doesn't work the item is available from Antique Electronic Supply and is part number P-H1590LB.Figures 7, 8, and 9, show construction of the transformer. These also show the three different coils I went through. The first and best was a Hammond 1 mH RF choke from AES. They discontinued it and I think Hammond has stopped making all of its RF choke and radio coil line. I can't find them on their website. I can't remember where I found the second one which was a 1.2 mH choke. It had a lower Q than the Hammond. But like the first it disappeared from the market. The third had even lower Q and came from Ocean State Electronics. I did my best to keep them in business but they went under anyway. Figure 9 shows the OSE choke. I'm not sure which of the remaining pictures is of the Hammond chokes

Figure 7

Figure 8

Figure 9
Figure 10 shows the 5 tube superhet which has a page of its own on this site. It is built on one of several solder breadboards I have. It performed quite well even with the poorest of chokes in the IF transformers.

Figure 10
Figure 11 shows the sweep of one of the transformers built with the Hammond chokes.

Figure 11
Band Pass Couplers.
Strictly speaking a double tuned transformer is a band pass coupler. It has a limited bandwidth and couples signal from the plate of one tube to the grid of the next. However I have chosen to give that name to a more complex circuit that is not magnetically coupled and can be so arranged to permit a front panel switch to select different bandwidths. Figure 12 below.

Figure 12
Note: The program mentioned is a filter design program which will be covered in excruciating detail farther down this page.
As shown the bandwidth may be changed by connecting a switch to select different values of C4. If RF chokes are used as the inductors, variable capacitors must be provided so all tuned circuits in an IF strip can be adjusted to the same frequency. When a filter of this type is implemented at VLF these capacitors can become rather large. A small trimmer may be used in parallel with a suitable amount of fixed capacitance as shown.
You are probably wondering what happened to L1 and L3 through L5. This is filter design convention. In a filter that begins with a T section the horizontal elements, dipoles as the programmer calls them, have odd numbers and vertical dipoles have even numbers. R1 is the plate resistance of the tube and if you use the filter design program described below it will be drawn horizontally and be dipole number 1. The parallel tuned circuit consisting of L2 and C2 make up dipole 2. Dipole 3 is C3 and so on up to L6 and C6. Dipole 7 is really there but it is just a piece of wire symbolized by a straight line. Dipole 8 is the load resistor. Filters of this kind require a load resistor in order to work properly. Note that C2 and C6 have been split into two capacitors a fixed one and a variable trimmer to allow the resonant frequency to be adjusted to the exact center of the IF.
Normally three such circuits are used in a receiver as shown in figure 13 below.

Figure 13
I have measured some real inductors on my Q meter and used the results to do some circuit simulations. I also have some silver mica high Q capacitors.
I have used the program to design a couple of filters one operating at 50 kHz and the other operating at 80 kHz. The latter is a close duplicate of the filters used in the NC-300. The fact that the values have come out somewhat similar is assurance that these designs might actually work when constructed. I intend to try this out soon.
Here are some example filters using the circuit of Figure 12.
50 kHz Band Pass Filter Design using 100 mH RF chokes. Design
Center
Freq.
(kHz)R1 L2 & L6 Q2 & Q6 C2 & C6 C3 & C5 C4 R8 Sim.
Center
Freq.
(kHz)-2 dB
BW
(kHz)-20 dB
BW
(kHz)Form
FactorInput
Impedance50 1 MΩ 100 mH 64 57 pf 47 pf 180 pf 560 kΩ 51.528 5.448 17.104 3.140 289 kΩ 50 1 MΩ 100 mH 64 57 pf 47 pf 270 pf 470 kΩ 50.951 3.639 14.343 3.941 516 kΩ 50 1 MΩ 100 mH 64 57 pf 47 pf 560 pf 680 kΩ 50.222 2.083 9.923 4.764 959 kΩ 150 1 MΩ 100 mH 64 57 pf 47 pf 1.5 nf 1.5 MΩ 49.649 0.959 5.598 5.837 1.626 MΩ 50 1 MΩ 100 mH 64 57 pf 47 pf 3.3 nf Inf. 49.515 0.586 4.027 6.872 1.712 MΩ 80 kHz Band Pass Filter Design using 25 mH RF chokes. Similar to NC 300. Design
Center
Freq.
(kHz)R1 L2 & L6 Q2 & Q6 C2 & C6 C3 & C5 C4 R8 Sim.
Center
Freq.
(kHz)-2 dB
BW
(kHz)-20 dB
BW
(kHz)Form
FactorInput
Impedance80 1 MΩ 25 mH 115 77.5 pf 83.6 pf 680 pf 300 kΩ 81.516 5.442 16.461 3.025 296 kΩ 80 1 MΩ 25 mH 115 77.5 pf 83.6 pf 1.2 nf 620 kΩ 80.635 3.317 10.504 3.16 430 kΩ 80 1 MΩ 25 mH 115 77.5 pf 83.6 pf 1.8 nf 390 kΩ 80.221 2.020 9.230 4.569 579 kΩ 80 1 MΩ 25 mH 115 77.5 pf 83.6 pf 4.7 nf 1 MΩ 79.672 1.068 5.593 5.237 1.00 MΩ 80 1 MΩ 25 mH 115 77.5 pf 83.6 pf 15 nf Inf. 79.423 0.500 3.145 6.290 1.29 MΩ ___________________________________________________
You may be puzzled by the points called out in the table, specifically -2 dB and -20 dB. Remember that this circuit is used in triplicate. These points will become -6 dB and -60 dB in the final IF strip. These are the figures used by receiver engineers. The -6 dB points define the bandwidth of the receiver. The -60 dB bandwidth specification characterizes the ability of the receiver to discriminate against strong interfering signals on frequencies near the one of interest. The form factor is the ratio of the -60 dB bandwidth to the -6 dB bandwidth. It defines the quality of the filter. Collins mechanical filters have a form factor of 1.2. Crystal filters will fall around 1.3 to 1.5. The values in the table are typical for LC filters.The 100 mH coils come from a bag of nominal 100 mH coils I got a long time ago from somewhere, I don't remember where. For a while I thought you could get them from Online Components but they have a fifty dollar minimum order. They are not interested in the hobbyist market. They went so far as to take down the page for the inductors after I placed a "small" order for them. Actually 40 mH coils would be better suited for 50 kHz. And I found them as well as the 100 mH coils from Digikey. 39 mH coils can be found at this link. 39 is close enough to 40 to keep me happy. Use this link for the 100 mH coils. Digikey also has the 25 mH coils for an 80 kHz if. They have Bourns coils which have a higher Q than the Hammond coils that are available from AES.
A Real Filter.
After receiving a few 25 mH chokes here is what I made of them. I selected the third entry in the 80 kHz section of the table above. The simulated bandwidth is 2.02 kHz. As you can see in the picture I constructed the filter using the old DeVry breadboarding connectors. Although no shielding or ground plain was used stability was not a problem. The red panel is taped to the workbench to make adjusting the trimmers a one handed process. The adjustment screw is bonded to the lug on the rounded end of the capacitor. Therefore a metallic screwdriver can be used for adjustment. That's a good thing because they do not turn easily. C2 and C6, 77.5 pf capacitors were made up of a fixed 47 pf and a 7 to 45 ceramic trimmer. C3 and C5 were changed from 83.6 pf to 82 pf. The capacitors used are 5% tolerance so they might be 83.6 pf. Placing the connector blocks far apart minimized stray capacitance and placing the coils at right angles minimized magnetic coupling.

Here is the frequency plot I obtained. I set up my digital function generator for a 16 kHz sweep centered on 80 kHz. The scope is a new acquisition. The first time I tried to read a time interval it threw me for a loop. Instead of the usual 10 horizontal divisions which were decreed by Tektronix more than 60 years ago it has 16 divisions. The horizontal scale is 1 kHz per division. With the sweep rate at 80 ms per div the sweep time is 1.28 seconds. I set this as the sweep time on the function generator. Then I set up my old analog function generator to trigger both the scope and the sweep of the digital function generator. I adjusted the amplitude so the pattern exactly filled 8 divisions vertically.

Let's look at the -20 dB and -2 dB bandwidths. -2 dB down from 4 divisions is 3.18 divisions. -20 dB down from 4 divisions is 0.4 divisions.
F2-20 = 85.8 kHz.
F1-20 = 76 kHz
BW-20 = 9.8 kHz
F2-2 = 81.2 kHz
F1-2 = 78.9 kHz
BW-2 = 2.3 kHzForm Factor = 4.26.
These figures are not out of line with the theoretical results calculated by the program.
While I had the filter assembled on my bench I took the time to explore some of the other bandwidths. It was easy enough to change C4 which is the square capacitor in the center of the panel. I don't think these are being made anymore. Changing it to 15nf and removing the 390 k ohm load resistor gave me a nice narrow passband. However it was 800 Hz instead of 500 as I wanted. Perhaps some tweaking of the capacitor might get it down to 500 Hz. On the other extreme the 5.5 kHz bandwidth came out as predicted. The shift in frequency was more striking on the o'scope screen than on the graphs. The low edge of the passband was at 80 and the upper edge was at 85.5 kHz.
All in all I would have to consider this experiment a success. If I ever do build a communications receiver it will very probably end with an 80 kHz IF, using filters of this type. If I do you will see it here.
The Program.
The filter design program I am using is one from the internet. It is called AADE Filter Design. For now it can be downloaded from here. There is one possible problem. If you go to the front door of this site there is an announcement that the operator of the site, and I assume the developer of the program, passed away in August of 2015. The program contains an update link which bypasses the front door and links into a side door. The html file is still on the server but it is no longer linked from the front page. I have no way of knowing how long this condition will continue to exist. If the above link is dead contact me and I will send you the install file.Low Q Capacitors are a Q Killer.
I found this out when I connected some capacitors in parallel with the variable capacitor in the Q meter to extend its range to lower frequencies, there are terminals provided for this, and found Q readings much lower than I had expected. Trying different types of capacitors I found out what to avoid.
- Any plastic film and foil.
- disc ceramic.
- Monolithic ceramic.
As you can see in some of the photographs above I have used the monolithic capacitors in the home brewed IF transformers. I didn't know they were such a problem. If you intend to duplicate the circuits above use only silver mica capacitors.
Using the filter design program.
There is one little thing that had me going in circles for a while. He uses a capitol K for the kilo prefix. Maybe that has changed but I learned it as a lower case k. Mega (M) milli (m) micro (u) and pico (p) are what you would expect. There is a setting in the setup menu for nano units if you want to use them.The main problem with the program as I experienced it is that the designs it produces often have impractical values. For example capacitors that come close to 1 uf that resonate with inductors of less than one uH. Or capacitors of less than 1 pf that resonate with inductors that have values in the henrys. However there is a way to override some of the program selected values so you can get the filter you want. Here is how to generate a practical filter design.
- From the "Design" menu select "Coupled Resonators". Then from the submenu select "Chebyshev".
- In the box that pops up enter the following values to duplicate my example. Later you can enter your own values.
- CF (center frequency) 50K. Be sure to type a capitol K.
- BW (bandwidth) 2.1K Bandwidth for SSB which is likely to be the narrowest BW I will be using.
- Order (number of tuned circuits 2.
- Apass (bandpass amplitude variation) 1. The default is .1 so be sure to change it.
- Click ENTER.
- Enter the value of the inductor 100 m. (100 mH). The default value of 31 uH will give you huge capacitors that wouldn't have enough Q to spell queen.
- In the box for Qu enter 60.
- click ENTER.
- Don't bother typing values for Zin and Zout. No matter what you type you won't get it. You won't even get the default values. You'll see.
- Click OK.
- Write down the values of the two resistors, the two inductors and the three capacitors. Round off the values to three or four significant digits. You will see that the value of C5 is a little too small to be practical.
- From the "Analysis" menu select "Voltage insertion Gain".
- F1 and F2 are the lower and upper limits of the graph. You might as well round them off to 40K and 60K respectively.
- Leave dB. 1 at 0 but change db2 to -40.
- Click "SET AS DEFAULT". If you forget to do this you will have to enter this data again.
- Click "ENTER".
- This is the frequency response of the filter.
- It might be a good idea to print this out for future reference. Changing from portrait to landscape under printer setup didn't change a thing.
- You will notice that there is a red cursor that follows your mouse along the graph. When you left click, the dB and frequency values where the cursor crosses the curve are shown in the information bar upper left corner of the graph window.
- Close the window by clicking on the X in the upper right of the window.
The filter design you will get is similar to that shown in figure 14. Note: He calls the filter elements dipoles. This is not a nomenclature I learned at the university of Florida. I guess this is another thing that has changed over the last 50 years. Because of space constraints I have abbreviated dipole as dp.

Figure 14
A word about what constitutes a dipole and takes up space in this diagram. Dipole 1 is the input resistor. In a real IF amplifier stage this will be the plate resistance of the IF tube. Dipoles 3 and 7 are short circuits, (pieces of wire). Dipole 2 is an open circuit. Don't ask me why the diagram is drawn in this way. I didn't write the program.
I have departed from his standard notation in that each component has a number associated with it so you won't have to look in two places to find it. Here are the values for the components in Figure 14.
R1 = 1.656 MΩ
C4 = 98.318 pf
L4 = 100 mH
Qu4 = 60
C5 = 3.137 pf
C6 = 98.318 pf
L6 = 100 mH
Qu6 = 60
R8 = 622.6 kΩ
The problem with this circuit is that C5 is too small to be practical. Remember that we want to change the bandwidth by switching a key capacitor in the circuit, namely C5. The switch would have more capacitance than the capacitors it is switching. To obtain practically sized capacitors we must do a π - T transformation on it. But first…

Figure 15
We split capacitors C4 and C6 into two equal parts C4A, C4B, C6A, and C6B. This reduces the effect of frequency change when the bandwidth is changed. National's solution to this problem was to use tapped inductors and change the inductance as the capacitance changed to keep the center of each passband on the same frequency. Hammarlund appears to just let it shift. Figure 15 shows the pi circuit we are going to transform into figure 16. The pi circuit consists of C4B, C5 and C6B. In the transformed circuit the useless dipoles have been eliminated and the first resonator has been moved to dipole 2 so its numbers are C2 and L2. The T network which comes out of the transformation consists of C3, C4, and C5.

Figure 16
The π - T Transformation.

Figure 17
Here is the whole thing in case you ever need it. But we only need to go one way from pi to T. Since the reactance is proportional to 1/C and reactance is part of impedance we don't want to use the Z equations. Z = 1/Y so we use the Y equations and since everything is proportional we simply substitute C for Y in the equations.
Referring back to figure 15 we can see that;
C4B is equivalent to YaWe also have the special case that C4B = C6B so Ya = Yb. Substituting into the Y equations on the left side of figure 17 we can solve for C3, C4 and C5 in figure 16.
C6B is equivalent to Yb
C5 is equivalent to Yc
C316 = C516 = ( C4B152 + 2 C4B15 C515) / C4B15
And
C416 = ( C4B152 + 2 C4B15 C515) / C515Where C316, C416, and C516, are C3, C4, and C5, in figure 16. And C4B15, and C515, are C4B, and C5, in figure 15. Remember that in figure 15 C6B = C4B so in a place where you think C6B should appear, it has been replaced by C4B.
Remembering that C4A15 and C4B15 each have half the value of the original C4 in figure 14 we have that C4B15 = 49.159 pf and C515 = 3.137 pf. When these values are substituted into the equations above we obtain,
C216 = C616 = 49.159 pf
C316 = C516 = 55.433 pf
C416 = 868.67 pf
Where C316, C416, and C516, are all the results of the pi to T transformation.
Now Let's Get Practical.
Now we will change to standard values and enter our filter back into the program and use the analysis function to figure out what we've got. C2 and C6 are made up of a fixed capacitor in parallel with a small trimmer capacitor so the value does not have to be standard. This will also make up for variation among inductors. R1 is the plate resistance of the tube. The 6BJ6, in my opinion the best choice for the if amplifier, has a plate resistance of 1 megohm at a plate voltage of 100 volts and 1.5 megohms at 250 volts. We will assume a lower voltage and a plate resistance of 1 megohm. R1 in the filter circuit is the plate resistance of the tube.R1 = 1.0 megohms.
C2 = 49.159 pf L2 = 100 mH
Qu2 = 64
C3 = 56 pf
C4 = 820 pf
C5 = 56 pf
C6 = 49.159 pf
L6 = 100 mH
Qu6 = 64
R8 = 620 kΩ
Now you are ready to enter the filter into the program. Select "NEW" from the files menu. The programmer did not implement any hot keys in this program so you will have to select from the menus. Then from the "UTILITIES" menu select "ENTER FILTER". You will be presented with a menu of parts. Select the resistor and enter its value of 1 megohm. The menu of parts will change presenting all parts as vertically oriented. Do not select a single inductor. Instead select the parallel inductor and capacitor. You will be asked for the values of the capacitor, the inductor, and the Q of the inductor. This is C2 and L2. Continue entering C3, C4, C5 and the parallel C6 and L6. For part 7 the straight line from the parts menu. Lastly enter R8 as listed in the parts list above. The analysis routine expects to find a vertical resistor at the output of the filter across which it makes the measurement for the analysis. If it doesn't find one it does something without an error message but it isn't right.
Now select "VOLTAGE EFFECTIVE GAIN" from the "ANALYSIS" menu. If you haven't closed the program since you looked at the plot of the original filter it will still have the defaults you set at that time. If you have closed it and reopened it you will have to set them again. Be sure to click "SET AS DEFAULT" after you enter the values in the boxes. Don't be concerned about the amount of attenuation. It is the attenuation of the filter plus, in dB, the attenuation of the two resistors R1 and R8 as if there was only a single connecting wire between them.
Note the instructions in the yellow panel at the bottom of the screen. Use this feature to set the limits of the plot the points where the response is down by about 2.5 or 3 dB from the peak of the curve. Use the cursor to read the exact attenuation at the peak. On the expanded plot read off the -2 dB points. They won't give you the 2.1 kHz bandwidth you specified. Remember we are using the -2 dB points because these filters run in threes so the total will be -6 which is where receiver engineers take the bandwidth measurement.
Now the fun begins. You can take that literally or sarcastically depending on how you feel about picking points and making calculations. I suggest you start a spreadsheet which can make the calculations for you so all you have to do is enter the data. There are two basic ways to find the bandwidths you want. One is to play with the value of C4 which will have a profound effect on the bandwidth and the other is to go back and do a design and keep running it until you get the -2 dB bandwidth you want. You don't have to transform the filter after each design. The response is the same before and after transformation.
Setting the Attenuation.
Every setting of a filter, value of C4, should have approximately the same attenuation. R8 is how you control the attenuation. In general the narrowest bandwidth will have the highest inherent attenuation. Set the value of R8 to 1000 megohms to find the attenuation for that setting. Then adjust the other settings to match within reason. It is said that 1 dB is the smallest change that can be detected by ear. In reality without a close A-B comparison the smallest detectable change is more like 2 or 3 dB depending on the listener. This will give you some leeway in adjusting the attenuation of each filter setting.Changing R8 also has a small effect on bandwidth. The attenuation seems to come out somewhere around 12 to 14 dB. To see the attenuation of the filter alone look at the voltage insertion gain under the analysis menu. It's pretty much a matter of trial and error. As you increase the value of C4 the band becomes more narrow and decreasing c4 makes it wider. You can play with the values from the table before launching into unknown territory on your own.
Conclusion.
Making an IF amplifier is no big deal unless you want it to have a narrow bandwidth that can be switched by a knob on the front panel of your receiver. If all you want is a receiver for casual short wave listening with no SSB capability you could build a tunable first IF receiver, convert from there to 455 kHz and call it a day. If you want a serious ham band only receiver you only need bandwidths of 2.1 kHz for SSB and 0.5 kHz for CW. If you want a general coverage receiver for both worlds you will need an IF amplifier with selectable bandwidths of 0.5, 2.1, 3.5 and 6 kHz, the 3.5 kHz for AM under difficult conditions and 6 for good quality on strong AM signals.For ham use you can still find Collins mechanical filters on eBay. This is the route I would recommend. If you have some experience with constructing crystal filters or are courageous enough to learn then go to it. There are lots of alternatives to making your own bandpass couplers.
Introduction
Image Rejection, IF Bandwidth, and Number of Conversions
Block Diagram
Construction Tips
Power Supply
Audio Amplifier
RF Amplifier and Preselector
Converters, Mixers, and Local Oscillators
IF Amplifiers and Band-pass Filters. You are here.
Detectors
AGC (Automatic Gain Control), and S Meter (Signal Meter)
Home Thank you for visiting my page at Angelfire.
Please come back and visit again!This site begun March 14, 2001
This page last updated January 27, 2016.