
For a verbal description click here.
Figure 1. Simple series circuit.
Electrical Fundamentals.
Before we can fly we must learn how to run. Before we can run we must learn how to walk. Before we can walk we must learn how to crawl. So get down on your hands and knees because we are going to deal with some batteries and resistors.
Basic DC Circuits.Everything has to add up.
I'll bet you were getting ready for Ohm's law. Not yet. Before we can deal with Mister Ohm we need to learn how to add and subtract.A fundamental law of electricity says that all the voltages around a circuit must add up to zero. When you go around a circuit and come back to where you started you are at the same voltage as when you started. Think of it this way. Suppose you get up from your seat in front of your computer and go outside of your house. In most houses you have to walk down 2 or 3 steps to get down to the level of your yard. If you live in an apartment building you may have to take the elevator down many floors to get to the outside. Then you climb a tree. You come to your senses, come down from the tree and go back inside hoping no one saw you. You go back to your computer and sit down.
Now what did you do? You stood up increasing the altitude of your body. you went outside decreasing your altitude. You climbed a tree increasing your altitude and then decreased it again when you came back down. You increased your altitude by going back into your dwelling and decreased it a little when you sat back down in your chair. You went up, down, up, down, up, and down, and you wound up back where you started. The sum of all the ups must be equal to the sum of all the downs. Or to put it more mathematically correct the sum of all the ups minus the sum of all the downs equals zero.
I hope it seems a little obvious to say that if you come back to where you started your net change in altitude is zero. It's the same with voltage, or potential as it is often known, if you go around an electric circuit and come back to where you started the sum of all the voltage ups is equal to the sum of all the voltage downs. It's time for a graphic.
Simple Series Circuit.

For a verbal description click here.
Figure 1. Simple series circuit.
Now you start walking across the resistors. Because there are two batteries in the circuit there is no way to be sure if we are going up or down. So lets not get too complicated right now. Let's say the battery on the left is 15 volts and the one on the right is 10 volts. So you are standing at 15 volts. Now if you walk across the resistors to the positive of the 10 volt battery you will be at 10 volts. That means you went down by 5 volts. Now how this 5 volts is shared among the 3 resistors depends on their relative values. But since we don't know Ohm's law yet we can't figure that out.
Now you walk down the 10 volt battery from positive to negative and you are back on the ground, electrically speaking, and you have descended by 10 volts. Notice that one of the batteries was a voltage rise and the other was a voltage fall. A battery isn't always a voltage rise, it depends on how you go across it.
The resistors were falls but if you walk around the circuit the other way when you walk across the resistors you will be increasing your voltage by 5 volts. So a resistor isn't automatically a fall, it can be a rise.
But the bottom line is the sum of the rises is equal to the sum of the falls. An equation stating this is
By the way, why would you connect a circuit like that? It's a battery charger and the battery on the right is being charged.
Solution
The closer you get to it the harder it is to define electric charge. But lets not get bogged down in philosophy. Electric charge is something that exerts a force at a distance.
There are two kinds of charges, positive and negative. Opposite charges attract and like charges repel.
If you have two baseballs each one having 1 coulomb of charge and they are 1 meter apart the force between them will be one Newton. The force is directly proportional to the product of the two charges, they don't have to be equal, and inversely proportional to the square of the distance between them.
Now in our circuit there is no place anywhere along the circuit where electrons can get in or out. They are not created or destroyed and they don't pile up at some point, remember like charges repel? They just keep going round and round. The number of electrons per second passing any point in the circuit is the same as the number of electrons per second passing any other point.
Current is the number of electrons per second passing a point. We could, if we wanted to, measure current this way. The charge on a single electron is 1.602 x 10-19 coulomb. Then one coulomb of charge is the reciprocal of the charge which is 6.242 x 1018 electrons. For those not yet familiar with scientific notation
1 amp of current = 6,242,000,000,000,000,000 electrons per second. If we did measure current that way we would constantly be dealing with large numbers so we use a more convenient form. Current is measured in amperes more commonly known as amps. One amp is one coulomb per second.
Solution
For a verbal description click here.
Remembering that electrons are physical objects that can't be created or destroyed you should be able to see that the sum of each of the individual resistor currents is equal to the battery current. If we call the battery current I, the current in R1 I1, the current in R2 I2, and the current in R3 I3 then we have the equation
Solution
Solution
For a verbal description click here.
From this we conclude that the current in a circuit is inversely proportional to the resistance.
Now we go back to the original resistor and start playing with the voltage. If we double the voltage the current doubles. If we cut the voltage in half, from its original value, the current is halved.
Conclusion, the current is directly proportional to the voltage. We can now write the equation
Solution
Solution
Solution
I actively discourage use of words like total and sum when doing resistors in parallel. As we speak so we think and using these words can get you confused. Now let's see, do I add when they are in series or parallel. Series!
Solution
Solution
and
P = V squared over R
* Yes, I know this is about DC circuits but the 120 volts of the power line is in RMS volts which is equivalent to 120 volts DC.
* Prior to 1965 pico was known as micro, micro.
To use this table you apply the formula
1.10. In Figure 1 if R1 = 22 ohms, R2 = 18 ohms, and R3 = 12 ohms, what is the current through R1?
Solution
1.11. In Figure 2 if E1 = 6 volts, R1 = 22 ohms, R2 = 18 ohms, and R3 = 12 ohms, what is the battery current?
Solution
1.12. In Figure 2 if the voltage across R1 is 77 volts, what is the voltage across R3?
Solution
1.13. In Figure 1 if the current in R3 is 28 m A, what is the current in (a) R2, (b) R1?
Solution
1.14. In Figure 1 the voltage across R1 is 1.9 volts, and the voltage across R2 is 0.8 volts. What is the voltage across R3?
Solution
1.15. In Figure 2 The current in R1 is 1.3 Amps, the current in R2 is 2.5 Amps and the battery current is 10 Amps. What is the current in R3?
Solution
1.16. In Figure 1 the voltage drop across R1 is 1.25 volts, the drop across R2 is 1.50 volts, and the circuit current is 0.682 m A. What is the resistance of R3? Hint. This is what I call a two level problem. You have to make an initial calculation and then use the result of that calculation to calculate the final answer.
Solution
1.17. In the circuit of Figure 2 the battery current is 0.675 amps, the current in R2 is 0.15 amps, and the current in R3 is 0.275 amps. The resistance of R3 is 200 ohms. What is the resistance of R1? This is a three level problem.
Solution
1.18. You want to connect a resistor substitution box across the 120 volt AC power line. Don't ask why, you just want to. The box uses 1 watt resistors. The values you can select are as follows
15 ohm, 22, 33, 47, 68, 100, 150, 220, 330, 470, 680, 1 k ohm, 1.5 k, 2.2 k, 3.3 k, 4.7 k, 6.8 k, 10 k, 15 k, 22 k, 33 k, 47 k, 68 k, 100 k, 150 k, 220 k, 330 k, 470 k, 680 k, 1 Meg ohm, 1.5 Meg, 2.2 Meg, 3.3 Meg, 4.7 Meg, 6.8 Meg, and 10 Meg ohm.
What is the lowest value you can set the box to without burning out a resistor (exceeding 1 watt)?
Scientific notation works by using powers of ten; 0.001, 0.01, 0.1, 1, 10, 100, 1000, etc. to multiply numbers that are allowed to have only the range of values from 1 to 10.
The first part is a number ranging from 1.0000 to 9.9999. In scientific notation it is not allowed to be outside of this range. It might be 9.9999999999999999999999999999999999999999999999999 but it never can be 10. The exponent is an integer which raises 10 to some power. Numbers in scientific notation look like this, 5.678 x 10+7. For example the number 1.23 x 10+1 = 12.3. 10+1 = 10 and 1.23 x 10 = 12.3. The number 4.567 x 10+6 is 4.567 x 1000000 which is 4567000. The number 4.7 x 10-11 = 0.000000000047. This last example should convince you that scientific notation is necessary in electronics. That's a 47 picofarad capacitor.
Here is a table of common values. You should be able to fill in the gaps.
* Normally nothing is written or printed for 10 to the power of 0.
(a) 5280
Solution
(a) 47.0 x 103
Solution
Those who are blind and use screen readers have a special problem with scientific notation. The problem is the way that screen readers read a web page. The number 3.56 x 103 will be rendered as 3.56 ex one hundred and three. If a plus sign is used e.g. 3.56 x 10+3 it is read as 3.56 ex ten plus 3. That's a little better but still not right. I hope the developers of screen readers will fix this problem some day but even if they do there are those older versions out there that still have problems. Any time I state a number in scientific notation I will follow it with the computer version, enclosed in parentheses, which can't be messed up by a screen reader. (Did I just say something about an unsinkable ship?) This will also teach sighted people to read scientific notation in computer notation.
(a) 1/4.7 x 10-6
What is current?
Many people teach current as being like water in a pipe. It's ok if you want to think of it that way but I would like to get you into thinking of electrons moving in a wire. Electrons are physical things. They have mass, they occupy space and they can't be created or destroyed. Picture them as very tiny Ping-Pong balls moving through a pipe. They have one more property, that is electric charge.
Optional.
When you see this heading you can skip it if it's too technical for you.
The current is the same everywhere.
In a simple series circuit like that of Figure 1 the current in any part of the circuit is the same as the current anywhere else in the circuit. Think of those little tiny Ping-Pong balls. They are not created in a battery and they are not destroyed in resistors. (I have known students who thought that.) They go around the circuit, in this case driven by the 15 volt battery on the left so they go counter clockwise. Electrons normally come out of the negative terminal of a battery and go into the positive terminal. When a battery is being charged instead of discharged the direction is reversed.
What's that we just learned?
In a series circuit the sum of all the voltage rises - the sum of all voltage drops is equal to zero. In a series circuit the current in any resistor, battery, or wire, is the same as the current in any other resistor, battery, or wire.
Example 1.2.
In Figure 1 if the current in R2 is 1.62 amps what is the current in; (a) the battery at E1, (b) R1, (c) R3, and (d) the battery at E2?
Simple Parallel Circuit.
Figure 2 shows the diagram of a simple parallel circuit.
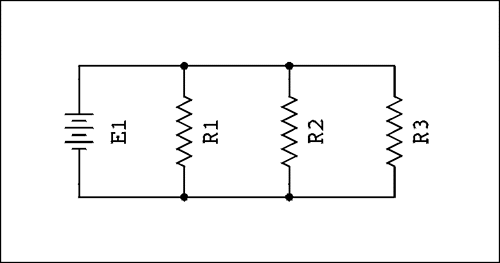
Figure 2. Simple Parallel circuit.
Electrons are coming out of the negative terminal of the battery. Some of them turn off and go into R1, some more go into R2 and what's left go into R3. The electrons pass through their respective resistors and are reunited again at the top terminal of the battery. You may have heard it said that "current takes the path of least resistance". NOT SO! The current will divide inversely as the resistance, but we are getting ahead of ourselves again.
Example 1.3.
In the circuit of Figure 2 the battery current I is 127 mA, I2 is 33 mA, and I3 is 45 mA. What is I1?
Example 1.4.
In the circuit of Figure 2 the battery voltage is 22.5 volts. What is the voltage across; (a) R1, (b) R2, and (c) R3?
Ohm's Law.
Just when you thought we'd never get here, here we are.

Figure 3. Simple circuit for Ohm's Law.
The ammeter and voltmeter are both indicating values. Now we double the value of the resistor. (This is a thought experiment so we don't have to say exactly how to go about this change. Also, the battery, ammeter, voltmeter, and resistor are perfect.) We find that the voltmeter reading remains unchanged but the ammeter reading is cut in half. Then we put in a resistor with half the value of the first resistor. We find that the current is now twice the original reading.
Example 1.5.
A measurement on a 2 cell flashlight shows that the bulb current is 350 milliamps. What is the hot resistance of the bulb's filament? One cell produces 1.5 volts.
Example 1.6.
You need a resistor that will drop 125 volts when the current is 26.6 milliamps. What is the value of this resistor in (a) ohms, and (b) kilohms?
Example 1.7.
If you connect a 25 k ohm (same as kilohm) resistor across an 850 volt power supply, how much current will flow? Give your answer in m A (same as milliamps).
Resistors in series and parallel.
In the textbook I wrote for my electronics class I derive everything. This is no college textbook so I won't go into that. If you want to know how the equations are arrived at I suggest you consult a book on the fundamentals of electrical engineering or enroll in an online electrical engineering course.
When two or more resistors are connected in series the total resistance is
Example 1.8.
Four resistors are connected in series. They are; 2.2 k ohm, 3.3 k ohm, 2.7 k ohm, and 2.4 k ohm. What is the equivalent resistance?
Example 1.9.
Four resistors are connected in parallel. They are; 2.2 k ohm, 3.3 k ohm, 2.7 k ohm, and 2.4 k ohm. What is the equivalent resistance?
Mathematics on a web page.
It's impossible to present even simple algebra in html code and not everybody knows the notation used by computer programmers. So I'm going to use words where necessary. For example because it is impossible to make a square root sign I will write "... the square root of 2". I could use graphics and I'll likely get around to doing that some time. The blind need not worry, I'll use alt= to keep it blind friendly.
Power
In an electric circuit the power is voltage times current.
Milliamps, kilohms, etc.
The possible values found in electrical and electronic circuits make it necessary to use some prefixes that represent multiplication by a number which is a power of ten. That is .01, .1, 1, 10 100, etc, etc. There is nothing for it but to memorize these. If you don't know these prefixes and their abbreviations any article about electronics will be so much Greek to you.
Spoken Prefix.
Multiplier.
Example.
Commonly used with.
Giga.
1,000,000,000.
Gigabyte.
Bytes, Cycles.
Mega.
1,000,000.
Megacycle.
Bytes, Cycles, Ohms, Watts.
kilo.
1,000.
kilohm.
Bytes, cycles, Ohms, Volts, Watts.
milli.
0.001.
milliamp.
Amps, Henrys, Volts, Watts.
micro.
0.000001.
microvolt.
Amps, Farads, Henrys, Volts, Watts.
pico. *
pronounced
peko.
0.000000000001.
picofarad.
Farads.
More Example Problems.
The problems will be given on this page but you must click a link to see the solution. I hope you will do your best to work out the answer for yourself before clicking the link. I'm not there to threaten you with a failing grade to make you do it. If you click the link before working the problem your not cheating me, It's no skin off my nose. By doing that you will cheat only one person, Y O U!
Scientific Notation.
If your not tired of messing around with all those zeros, you will be when you get well into the AC chapter.
Eventually you are going to get disgusted and throw up your hands saying "There's got to be an easier way." When you say that, a little voice will answer "There is. It's called scientific notation." You may get frustrated and give up the first time you work through this section but after you do a few of the example problems in the next chapter I predict you will come back here with a determined look on your face, saying through clenched teeth "I'm not going to let this thing lick me".
How it works.
A number expressed in scientific notation is broken into two parts. They have names but it isn't really important that you remember them. Just learn how they work. The first part of the number is called the mantissa. That probably comes from Latin, Greek, or one of those highly incomprehensible languages. The second part is called the exponent.
Powers of Ten.
I'm sure you already know that 10 squared is 100 and 10 cubed is 1000. 10 to the minus 1 power is 0.1, 10 to the minus 2 power is 0.01, and oh yes, 10 to the 0 power is 1. 10 to any integer power, positive or negative, is a number consisting of a 1 and a number of zeros.
How the computer sees it.
It's not always easy to make the computer show that little number above and to the right of the 10. It is possible in HTML but not in some other programming languages so I'm going to educate you from the beginning to read and write it the way the computer does. The number 2.34 times 10 to the power of 2 is represented as 2.34 e 2 or 2.34 e+2. The number 7.65 times 10 to the minus 3 power is 7.65 e-3.
Power of 10
Computer Notation
Number
10-12
e-12
0.000000000001
10-9
e-9
0.000000001
10-6
e-6
0.000001
10-3
e-3
0.001
10+0 *
e 0 *
1
10+3
e 3
1000
10+6
e 6
1000000
10+9
e 9
1000000000
10+12
e 12
1000000000000
Example 1.19.
Express the following numbers in scientific notation.
(b) 26.48
(c) 0.0000036
(d) 525.8
(e) 0.0162
(f) 74890000
(g) 0.000000125
(h) 152000
(i) 9730000000
(j) 0.0000000000022
Keeping things straight.
Sometimes it is necessary to move the decimal point to make the first part of the number fall between 1 and 10. People often get confused which way to change the exponent when moving the decimal point. Think of it this way. You don't want to actually change the value of the number, you just want to move the decimal and change the exponent. The trick is "smaller, larger" or "larger, smaller". If you make the first part smaller, make the second part larger. If you make the first part larger, make the second part smaller.
Lets take an example. Suppose you did a calculation and you got 567.8 x 10-6. to make it a legal number in scientific notation you do this.
smaller, larger
5.678 x 10 -4
Example 1.20.
Fix each of these numbers to be correctly expressed in scientific notation.
(b) 0.025e-6
(c) 28.7 x 106
(d) 365 x 10-12
(e) 455e3
Engineering Notation.
Many of the programs I have written use engineering notation. That confines the exponents to integers which are divisible by 3 and the first part can range between 1 and 999.99999999999 but never 1000.
The powers divisible by 3 are used because they all have names such as milli, Mega, etc. Unless you have a scientific calculator which will work in engineering notation I recommend you stick to the scientific kind.
Most people have calculators that are meant to work in dollars and cents so scientific notation is best. You can use the calculator to do the multiplication and division and keep track of the power of ten separately.
The Four Arithmetic Functions.
The classic four arithmetic functions are addition, subtraction, multiplication, and division. Performing these in scientific notation is not hard, like anything it's easy if you know how. So here's how.
Addition and subtraction.
To add or subtract two numbers you must move the decimal point and change the exponent until the exponents are equal. For example to add
Smaller, Larger
1.83 x 10-5
Multiplication.
To multiply two numbers in scientific notation you multiply the mantissas (first part) and ADD the exponents. For example,
Division.
To divide two numbers you divide the mantissas in the usual way. Then you subtract the exponent in the denominator from the exponent in the numerator. For example,
Example 1.21.
Perform the following calculations and express the numbers in correct form.
(b) 2.5 x 10-3/4.7 x 103
(c) 1.5 x 106 x 2.2 x 10-6
(d) 1.2 x 103 + 8.2 x 102