What's your
actual treestand shooting distance?
What's your actual treestand
shooting distance?
Question:
What Distance do I shoot if I'm 20 feet up in a tree and my target is 20 yards
away?
More or less than 20 yards?
Answer:
Use the actual flat distance from the base of the tree to the target.
Why? Your arrow naturally falls to the ground as a result of Gravity. Gravity will pull your arrow towards the ground for every vertical inch of travel For reference sake, we will call this your "gravity distance" Your actual distance from you to the target is actually farther away than your gravity distance. To see and example lets look at the simple geometry problem below. I know for many of you, your old geometry book is either in the trash or has dust on it 2 inches thick! So I will start from the
basics and lead you through this.
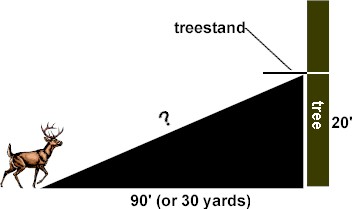
As shown above in picture #1, your arrow travels an actual unknown distance as marked by the "?" but is only pulled towards the
ground by gravity over 30 yards. So here's the tricky question...How far do I
shoot the deer? In this example, you would shoot the deer for 30 yards. Now
what if sitting there in your cozy treestand with a Bushnell 400 range finder and you put a bead on the side of that monster buck standing there....how far will the range finder read?
Well here's where your old geometry book comes in handy. The equation below,
shown in picture #2, is the "ye-old" Pythagorean theorem.

Before we begin to plug & chug your numbers
into the equation, it is important to remember that we must use equal units of input. Therefore we must either convert all our numbers into yards or feet
measurements. For my example we will use feet as our unit of measure. To begin we must know the height which is equal to 20 feet. The first part of this
equation is to square the height OR...( 20 x 20 = 400)
Our height squared number is 400. Next is our yardage. Since picture #1 shows 30 yards we will use that. 30 yards is the same as 90 feet so the next part of
our equation is (90 x 90 = 8100). Our yardage squared number is 8100. Next we add the two numbers together for a total of 8500 (400 + 8100 = 8500). Finally we
take the square root of our new number and come up with 92.195445. Now since we are using feet as our unit of measure we must convert that into yards for a
distance of (92.195445 / 3 = 30.73) 30.73 or approximately 31 yards. So in this example, your Bushnell would read 31 yards, but we still shoot the deer for 30 yards.
Question:
Why does everyone keep telling me to subtract yardage from my shot when shooting from a treestand?
Answer:
Most treeestand shots give you the optical illusion
of being further away.
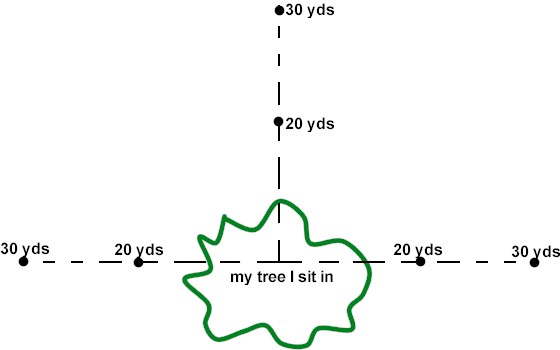
Before you climb into your tree or before hunting season starts you may want to
take a few minutes associating certain trees, stumps or rocks as a given
distance away. I will do one of two things before I begin my hunting season. I
will put either wooden stakes in the ground around my stand or will make mental
notes of other trees around my stand that are exact yardage of 10, 20 and 30
yards away. To see the pattern in which I layout my stakes see the picture #3
below.
 Brought to you bt the people at Archery Dot Net
Brought to you bt the people at Archery Dot Net