2- ERROS NA ANÁLISE CLÁSSICA

2.1.-COMPLEMENTOS DE ESTATÍSTICA

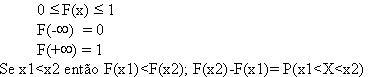
Variável aleatória a uma função que costuma ser representada por X, cujo valor é um número real determinado pelo resultado de uma experiência aleatória.

Exemplos:

• percentagem de íons de nitrato na água de um reservatório
• Nº de glóbulos brancos por unidade de volume de sangue humano

As variáveis aleatórias podem ser de dois tipos:

• Discretas se tomam valores num conjunto finito ou infinito mas numerável
• Contínuas se podem tomar qualquer valor real num intervalo

Para uma dada experiência aleatória podemos estar interessados no estudo de de uma única característica, ou seja numa variável aleatória unidimensional, ou pelo contrário num conjunto de característica, tratando-se assim de uma variável aleatória multidimensional

. Um conceito que nos permite compreender o fenômeno associado à experiência, descrita pela variável aleatória é o de:

1. Função de distribuição ou distribuição cumulativa
   . Dada uma variável aleatória X designa-se por F(x) a aplicação :
   
2. Propriedades da função de distribuição
   

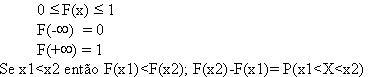
Para as variáveis aleatórias discretas chama-se distribuição de probabilidade ao conjunto dos pares (xi,pi) em que pi é a probabilidade de X tomar o valor xi. Neste caso,

Para as variáveis aleatórias contínuas chama-se função densidade de probabilidade à função f(x) contínua e positiva, tal que: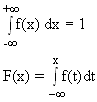

Chama-se, para as variáveis aleatórias contínuas :
Valor médio, esperança matemática valor esperado ou média, e representa-se por

Propriedades do valor médio:

E(a)=a
E(a+bX)=a+bE(X)
E(X+Y)=E(X)+E(Y)
Se X e Y forem independentes E(XY)=E(X).E(Y)

O valor médio é uma medida do centro de uma distribuição. Uma medida de dispersão em relação ao valor médio, é-nos dada pela variância, representada por ², e definida por E[(X-m)²], a chama-se desvio padrão.

Propriedades da variância

Var(X)0
Var(aX+b)=a2Var(X)
Se X e Y forem independentes Var(X+Y)=Var(X)+Var(Y)

À variação conjunta de X e Y chama-se Covariância e designa-se por Cov(X,Y) o valor de E(XY)-E(X)E(Y). Desta definição resulta que o valor da covariância depende das unidades em que se exprimem as variáveis aleatórias X e Y. Deste modo introduz-se um parâmetro que caracteriza a intensidade da ligação entre X e Y, o coeficiente de correlação, designado por e definido por . Este valor está compreendido entre -1 e 1. Se X e Y são independentes então =0>.
Das propriedades do valor médio e da variância podemos facilmente deduzir quais os parâmetros da variável aleatória , obtida pela média de variáveis aleatórias com a mesma distribuição, com parâmetros , em que o valor médio e a variância são, respectivamente;

Vamos em seguida descrever sumariamente algumas variáveis aleatórias contínuas, nomeadamente com distribuição :

1. Normal
2. Qui-Quadrado
3. t de Student
4. F de Snedecor

Distribuição Normal

A distribuição normal surgiu no século XVIII ligada ao estudo de erros de medições repetidas de uma mesma quantidade (replicadas). As suas propriedades matemáticas foram estudadas por DeMoivre, Laplace e Gauss, sendo por este fato esta distribuição conhecida por distribuição de Gauss. 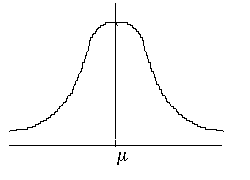As principais razões da sua importância prendem-se com o fato de muitas variáveis biométricas serem aproximadamente normais, de mesmo variáveis não normais poderem ser transformadas nesta, ou ainda, neste caso a parte central ser razoavelmente bem aproximada por uma normal.A normal representa-se por N (µ,) .

f.d.p.=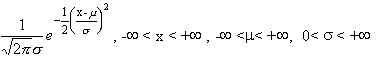

Propriedades da distribuição normal

Simetria relativamente a µ, f(µ+a)=f(µ-a)
Unimodal - moda = µ
Maximizante em µ,

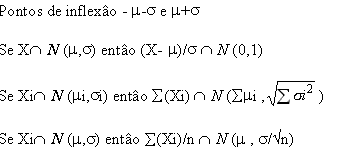
As propriedades anteriores mostram que a soma de Normais ainda é uma normal. Mais ainda o seguinte teorema mostra-nos que a distribuição aproximada da soma de n variáveis aleatórias independentes e identicamente distribuídas, é a de uma normal, segundo certas condições.

Teorema do Limite Central

Seja {Xn} uma sucessão de n variáveis aleatórias i.i.d. , com valor médio µ , e variância ²(finita). A variável aleatória Sn=(Xi) tem distribuição assintóticamente normal, com parâmetros nµ e . Ou seja para um valor de n suficientemente grande, a distribuição de Sn é N(nµ , ), e escreve-se Sn ~ N(nµ ,).

Donde se obtém que, a média de n variáveis aleatórias é: (Xi)/n~N(µ,)

Distribuição Qui-Quadrado

Esta distribuição é muito usada em inferência estatística, sendo um caso particular da função gama. Entre outras utilizações, é de realçar a sua aplicação no estudo da variância de uma população a partir de uma amostra.

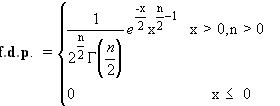
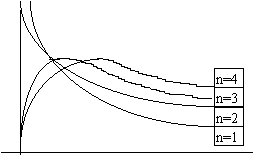
Esta função como, como se pode observar pela f.d.p. fica perfeitamente especificada pelos graus de liberdade ,n . Representa-se por .

Alguns resultados importantes relativos a esta distribuição, são:

A soma de funções com distribuição qui-quadrado, tem distribuição qui-quadrado com grau de liberdade igual à soma dos graus de liberdade dessas distribuições:

Se Z tem distribuição normal reduzida, então o quadrado de Z tem distribuição qui-quadrado com um grau de liberdade:

Distribuição t de Student

Esta distribuição foi introduzida por William Gosset em 1908, que publicava os seus trabalhos sob o pseudônimo de Student, para não divulgar à concorrência da fábrica em que trabalhava, a utilização dos métodos estatísticos nos processos de fabrico. Tal como a distribuição anterior, esta distribuição tem um papel importante na inferência estatística, e fica identificada por um parâmetro, o grau de liberdade. A variável aleatória com a distribuição de Student representa-se por t_(n).

Propriedades e resultados relativos à distribuição t de Student

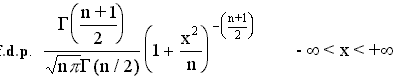
Simétrica
E(t)=0;
Var(t)=n/(n-2) para n>2
unimodal
semelhante à normal reduzida
Se

Distribuição F de Snedecor

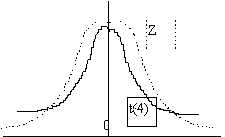
Esta distribuição em conjunto com a do Qui-Quadrado e t de student, forma um conjunto de distribuições teóricas indispensáveis na resolução de problemas de inferência estatística. A distribuição F, encontra um largo campo de aplicação em problemas relativos à análise de variância. Diz-se que uma variável aleatória tem distribuição F, e escreve-se X~F(m,n) se a sua função densidade de probabilidade for definida por:

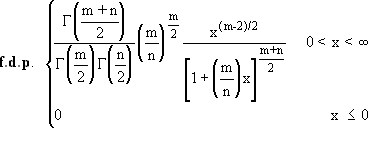
Propriedades e resultados relativos à distribuição F

Apontamentos sobre inferência estatística

2.2.- PROPAGAÇÃO DE ERROS ALEATÓRIOS

Em trabalho experimental, o cálculo de um valor final pode ser resultado da combinação de um conjunto de valores observados. Este cálculo pode envolver operações como a soma, quociente ou produto, ou ainda a sua combinação. É de salientar que o efeito destas operações em erros aleatórios e sistemáticos é completamente diferente, porque os erros aleatórios de certa forma cancelam-se, enquanto que os erros sistemáticos, uma vez que apresentam uma tendência, reproduzem-se ao longo destas operações. Supondo que x é o resultado de a+b, onde a e b têm um erro sistemático de 1. O valor atribuído a x herda um erro de valor 2. No entanto se a e b tivessem subjacente um erro de ±1 o erro de x não seria de ±2 . Importa pois conhecer a forma como interagem os erros aleatórios e sistemáticos num conjunto de operações.

A expressão geral do erro aleatório inerente a um valor y resultante de operações definidas por uma função P(ui) pode ser definido da seguinte forma:

A demonstração deste resultado não é apresentada uma vez que a teoria necessária à sua demonstração não se enquadra nos objetivos desta disciplina. Mais ainda convém realçar que este resultado é uma simplificação de uma expressão matemática mais rigorosa. A sua apresentação corrente na bibliografia de quimiometria justifica a perda de rigor em função da praticabilidade. Nesta perspectiva é desculpável o abuso de notação no uso de -s - como interpretador do erro.

2.3.- PROPAGAÇÃO DE ERROS SISTEMÁTICOS

A propagação dos erros sistemáticos determina-se de forma análoga aos erros aleatórios, com ausência do sinal de módulo, uma vez que estes erros têm um sinal determinado. O valor do erro sistemático de cada membro do cálculo final, é identificado pela letra

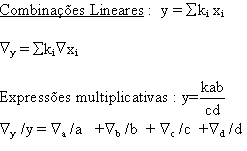
2.4. TESTES PARA COMPARAÇÃO DE MÉTODOS

. Uma das formas de selecionar um método analítico, é comparando vários métodos de acordo com as suas características. A substituição de um método por outro faz-se normalmente porque este último é menos dispendioso, mais rápido ou por outras características que o tornam mais atrativo. No entanto uma decisão deste tipo não é levada acabo sem um estudo da precisão e ausência de erros sistemáticos. A forma mais simples de determinar a acurácia de um método, é analisando um material padrão ou standard para o qual a concentração do da substância a analisar é conhecida. A diferença entre o valor obtido pela média de replicadas e o valor correto dar-nos-á uma indicação da existência ou não de viés. Se a diferença não for significativa os desvios podem ser considerados como resultados de erros aleatórios, caso contrário o erro pode ser usado como um estimado do erro sistemático. Na ausência de material standard a comparação pode ser estabelecida em relação a um método para o qual é conhecida a ausência de erros sistemáticos. No entanto a precisão do método nos casos descritos estará a ser determinada apenas para o material utilizado. Este procedimento não será incorreto se a extrapolação não suscitar ambigüidades. Caso contrário o teste mais correto decorrerá de várias análises para diferentes produtos.

Em seguida apresentam-se testes para validação de um método por comparação:

• com um resultado conhecido (uma amostra ou duas amostras independentes)
• com um método conhecido (amostras emparelhadas)

Avaliação do viés de um método por utilização de material padrão ou standard (identificação de erros sistemáticos)

Quando se analisa uma amostra standard, por exemplo como as propostas por organizações como a ASTM (American Society of Testing and Matterials), NBS ( National Bureau of Standards) ou a BCR (Bureau Communautaire de Reference), por um novo método, há que decidir se o resultado difere significativamente do correto. O termo significativo em estatística é estabelecido a partir do conhecimento da função de distribuição da variável aleatória (estatística de teste) utilizada para comparação dos resultados. Se a probabilidade de ocorrência do valor observado for pequena, isso corresponde à não aceitação da hipótese estudada, ou seja a de que os valores comparados não diferem significativamente. A probabilidade de rejeitar uma hipótese corresponde ao nível de significância do teste, sendo um valor a, normalmente igual a 0.1 ou 0.05.

Comparação com um valor conhecido com erro aleatório negligenciável (uma amostra)

Neste primeiro caso a hipótese em estudo pode ser posta da seguinte forma :

Dado uma amostra de dimensão n poderemos afirmar que o seu valor médio µ é igual a mµ₀ ? = média dos n resultados obtidos pelo novo método ; µ₀ = valor correto

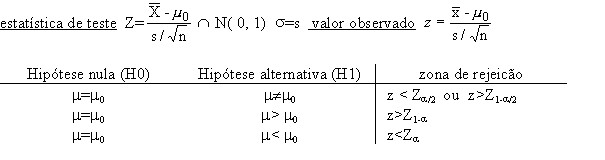
a) Grandes amostras (n>30)

Para grandes amostras pelo teorema do limite central estaremos a testar a hipótese de ter uma distribuição Normal com valor médio µ₀ e desvio padrão sendo “s” um bom estimado de .

b) Pequenas amostras

Para pequenas amostras o teorema do limite central já não é aplicável mas utilizando a hipótese de normalidade de é uma normal reduzida, ou seja tem uma distribuição com valor médio µ igual a µ:₀ e desvio padrão igual a .

Então

Exemplo: Para investigar um novo método utilizou-se um material padrão cuja concentração de Pb é conhecida (0.340 mg). Foram realizadas 15 replicadas pelo método a testar tendo-se obtido o seguinte resultado:
0.380; 0.346; 0.291; 0.278; 0.404; 0.331;0.409; 0.285; 0.361; 0.268; 0.306; 0.243; 0.316; 0.223 ; 0.299.
A média obtida difere significativamente do valor real, existe evidência de erros sistemáticos no método?
= 0.316 ; s=0.056

t_0.05= -1.761 e t_0.95=1.761 como |t_obs|=1.660<1.761 não se rejeita a hipótese de que a diferença não é significativa. O nível de significância foi de 0.1.

Comparação com um valor conhecido cujo erro aleatório não é negligenciável (duas amostras independentes)

Neste segundo caso estamos a comparar o valor obtido pelo método a testar com um valor conhecido para o mesmo produto que estamos a analisar mas por um outro método certificado. A questão será posta, neste caso, nos seguintes termos:

Será que de duas amostras independentes de dimensão n₁ e n₂ com médias respectivamente e e variâncias s₁ e s₂ provêm de uma mesma população com valor médio µ , ou seja os seus valores médios µ₁ e µ₂ são iguais a µ?
a) Grandes amostras (n>30)

Para grandes amostras pelo teorema do limite central estaremos a testar a hipótese de ₁ e ₂ terem uma distribuição normal com valor médio µ₁ e µ₂ iguais a µ e desvio padrão respectivamente ₁/₁ e ₂/₂ sendo “s1 e s2 ” estimadores dos respectivos desvios padrões. Neste caso podemos considerar a diferença das duas normais, que ainda será normal com valor médio µ-µ=0 e variância s₁²/n₁+ s₂²/n₂.

Exemplo : Uma amostra é analisada num estudo inter-comparativo para a determinação de um composto A tendo-se obtido os valores para a média e variância respectivamente 32.6 e 6.55 com amostras de dimensão 36. O analista analisou uma amostra com o seu próprio método tendo obtido para 30 replicadas os valores : 31.6 para a média e 4.05 para a variância. Pender-se-á concluir que o método investigado produz resultados iguais ou inferiores aos do estudo inter-comparativo?

como 1.776 > 1.645 rejeitamos a hipótese H0 de igualdade de valores médios havendo evidência de que que µ₁ poderá ser maior que µ₂

b) Pequenas amostras

Exemplo : Utilizando o exemplo anterior mas agora considerando que que n₁=11 e n₂=13

e que a hipótese de normalidade e homogenidade está verificada.

como t_0.95=quantil 0.95 de uma t(22)=1.717 e 1.071<1.717 não rejeitamos a hipótese de igualdade de valores médios.

Comparação de dois métodos para a mesma amostra (amostras emparelhadas)

Outro caso em estudo refere-se ao estudo de n amostra de diferentes concentrações, ou não, por dois métodos. No primeiro caso, o teste que desenvolveremos só será aplicável se os erros não forem proporcionais às concentrações dos produtos e, em caso de erros sistemáticos eles sejam constantes. A formulação da comparação dos dois métodos pode ser posta da seguinte forma:

Dados os dois conjuntos de dados, o valor da diferença entre cada par de observações terá uma distribuição com valor médio zero?

Considere-se para cada par de observações a diferença di = x1_i-x2_i . Para testar esta hipótese temos mais uma vez que fazer uma distinção entre pequenas e grandes amostras.

a) Grandes amostras (n>30)

Para grandes amostras pelo teorema do limite central estaremos a testar a hipótese de ter uma distribuição normal com valor médio µ_D=0 e desvio padrão / sendo “s” um bom estimado de

.

b) Pequenas amostras

Para pequenas amostras o teorema do limite central já não é aplicável mas utilizando a hipótese de normalidade de podemos recorrer à estatística que tem uma distribuição t(n-1) porque Z=/(/) tem distribuição de uma normal reduzida ou seja tem uma distribuição com valor médio igual a 0 e variância a ²/n e assim, sendo a distribuição de (n-1) S²/² é um .

Exemplo : A composição do composto A é analisado em dez amostras por um método padrão R, e um método a testar T. Será que os dois métodos produzem resultados diferentes?

Próximo

Anterior

Inicio