Στην καρτεσιανή γεωμετρία τα σημεία περιγράφονται με έναν απόλυτο και συστηματικό τρόπο. Η γεωμετρία αυτή έχει σημαντικές διαφορές με τη γεωμετρία της χελώνας. Η LOGO περιέχει εντολές που υποστηρίζουν την καρτεσιανή γεωμετρία. Ο Papert θεωρεί ότι είναι πολύ σημαντικό να καταλάβουν τα παιδιά τις σχέσεις ανάμεσα στη γεωμετρία της χελώνας και την καρτεσιανή γεωμετρία.
Το πρόβλημα όμως που υπάρχει είναι ότι η καρτεσιανή γεωμετρία παρουσιάζει
μεγάλη δυσκολία για να κατανοηθεί από τα παιδιά. Έρευνες που έγιναν [2],
έδειξαν ότι υπάρχει μεγάλο χάσμα ανάμεσα στη γεωμετρία της χελώνας και
στην καρτεσιανή γεωμετρία. Παρόλο που τα παιδιά που ασχολούνται με τη γεωμετρία
της χελώνας εφοδιάζονται με κάποιο "σχήμα" σκέψης, είναι πάρα πολύ δύσκολο
για αυτά να καταλάβουν το καρτεσιανό γεωμετρικό σύστημα και τη σχέση του
με αυτό της γεωμετρίας της χελώνας. Όπως αναφέρει ο Papert, αυτό οφείλεται
στη διαφορετική φύση των δύο αυτών γεωμετρικών συστημάτων. Για να γίνει
η σύνδεση μεταξύ της καρτεσιανής και της γεωμετρίας της χελώνας, είναι
απαραίτητη η ύπαρξη ενός νοητικού σχήματος που θα γεφυρώσει το χάσμα που
υπάρχει μεταξύ τους.
Θεωρούμε, στο επίπεδο, δύο ευθείες x’Ox και y’Oy πάνω στις οποίες έχουμε
ορίσει μια μονάδα μέτρησης και τις οποίες θα καλούμε "άξονες συντεταγμένων".
Το O λέγεται αρχή των συντεταγμένων ή απλά αρχή. Τους ημιάξονες Ox και
Oy (που στο σχήμα υποδεικνύονται με βέλος) θα τους λέμε θετικούς ημιάξονες
και τους Ox’ και Oy’ αρνητικούς.

Τώρα, από τυχόν σημείο Α του επιπέδου φέρουμε ευθείες παράλληλες στους δύο άξονες οι οποίες τέμνουν αυτούς στα σημεία Ax και Ay. Θα καλούμε τετμημένη ή πρώτη συντεταγμένη του σημείου Α, το αριθμό x του οποίου η απόλυτη τιμή ισούται με το μήκος του ευθυγράμμου τμήματος OAx και θα θεωρούμε το x θετικό αν το σημείο Ax κείται στο θετικό ημιάξονα Ox και αρνητικό αν το Ax κείται στον αρνητικό ημιάξονα Ox’. Ακριβώς ανάλογα ορίζεται η τεταγμένη ή δεύτερη συντεταγμένη y του σημείου Α. Το ζεύγος (x,y) ορίζει "πλήρως" το σημείο Α και αντίστροφα σε κάθε ζεύγος αριθμών (x,y) R2 αντιστοιχεί ένα σημείο Α του επιπέδου με συντεταγμένες x,y. Δηλαδή, υπάρχει μία "1-1" και "επί" αντιστοιχία μεταξύ των σημείων ενός επιπέδου και των στοιχείων του συνόλου R2={(x,y):x,y ε R} (ευκλείδειος χώρος διάστασης 2).
Ιδιαίτερα, αν οι άξονες x’Ox και y’Oy είναι κάθετοι τότε, μιλάμε για ένα ορθογώνιο σύστημα συντεταγμένων. Εξάλλου, αν τα ευθύγραμμα τμήματα που θεωρήσαμε σαν μονάδες επάνω στους άξονες έχουν ίσα μήκη (:μπορούν να συμπέσουν αν τεθεί το ένα πάνων στο άλλο), τότε λέμε ότι έχουμε ένα ορθοκανονικό σύστημα συντεταγμένων.[4]
Αυτή βλέπει τον κύκλο καθώς πηγαίνει κατά μήκος του και είναι "τυφλή" σε οτιδήποτε είναι έξω από αυτόν. Αυτή η μία πολύ σημαντική ιδιότητα που κάνει τη γεωμετρία της χελώνας να ονομάζεται "εσωγενής".[1]
Στη καρτεσιανή γεωμετρία, τα σημεία ορίζονται σύμφωνα με την απόστασή τους από ένα συγκεκριμένο σημείο, που είναι σταθερό. Έτσι υπάρχει ένας συστηματικός και απόλυτος τρόπος περιγραφής των σημείων. Η περιγραφή τους δίνεται σε σχέση με ένα σημείο, που είναι η τομή δύο κάθετων, βαθμολογημένων ευθειών τις οποίες θεωρούμε σαν άξονες συντεταγμένων. Σε αυτή τη γεωμετρία τα σχήματα περιγράφονται από αλγεβρικές εξισώσεις, που συνδέουν το σύνολο των σημείων τους με την αρχή των αξόνων.
Μία βασική διαφορά ανάμεσα στην εσωγενή γεωμετρία και την καρτεσιανή βρίσκεται στην έννοια των εσωγενών ιδιοτήτων των γεωμετρικών σχημάτων. "Μία εσωγενής ιδιότητα είναι αυτή η οποία εξαρτάται μόνο από το εν λόγω σχήμα και όχι από τη σχέση του σχήματος με ένα πλαίσιο αναφοράς." [5]
Μία άλλη διαφορά τους είναι ότι η εσωγενής γεωμετρία περιγράφει γεωμετρικά αντικείμενα σε σχέση με τις διαδικασίες και όχι σε σχέση με εξισώσεις. Περιγράφοντας γεωμετρικά σχήματα με τη χελώνα έχουμε πρόσβαση σε μία μεγάλη περιοχή διαδικαστικών μηχανισμών (όπως η επανάληψη) τα οποία είναι δύσκολο να κατανοηθούν με την παραδοσιακή αλγεβρική περιγραφή.
Επιπλέον, η περιγραφή των αντικειμένων, μέσα από τις διαδικασίες, εύκολα τροποποιείται με πολλούς τρόπους. Αυτό κάνει την εσωγενή γεωμετρία ένα παραγωγικό χώρο για εξερεύνηση μαθηματικών εννοιών.
Το επόμενο σχήμα δείχνει μια οθόνη υπολογιστή με ένα grid από οριζόντιες
και κάθετες γραμμές. Το σημείο το οποίο συναντούνται οι δύο έντονες συναντούνται,
ονομάζεται "αρχή των αξόνων". Αναπαρίσταται από τους αριθμούς [0 0]. Για
άλλα σημεία ο πρώτος αριθμός (συντεταγμένη x) είναι η οριζόντια απόσταση
από την αρχή των αξόνων μέχρι το σημείο και ο δεύτερος αριθμός (συντεταγμένη
y) είναι η κάθετη απόσταση από την αρχή των αξόνων μέχρι το σημείο. Μια
θετική x συντεταγμένη σημαίνει ότι το σημείο είναι δεξιά από την αρχή,
μία αρνητική x συντεταγμένη σημαίνει ότι το σημείο είναι αριστερά από την
αρχή. Παρόμοια, μια θετική y συντεταγμένη σημαίνει ότι το σημείο βρίσκεται
πάνω από την αρχή ενώ μια αρνητική y συντεταγμένη σημαίνει ότι είναι από
κάτω.

"Η LOGO βέβαια, μας δίνει τη δυνατότητα να αναφερόμαστε σε σημεία με τις καρτεσιανές τους συντεταγμένες, χρησιμοποιώντας μια λίστα από δύο αριθμούς. Η αρχή των αξόνων είναι το σημείο όπου πηγαίνει η χελώνα όταν καθαρίζουμε την οθόνη"[6].
Το πρωταρχικό εργαλείο για να κάνουμε γραφικά στη LOGO με καρτεσιανό τρόπο είναι η εντολή SETPOS (από το SetPosition). Η SETPOS απαιτεί μια είσοδο, η οποία πρέπει να είναι μια λίστα από δύο αριθμούς. Το αποτέλεσμά της είναι να μετακινηθεί η χελώνα στο σημείο της οθόνης σε αυτές τις συντεταγμένες. Ένα μικρό παράδειγμα χρήσης της SETPOS είναι η ακόλουθη σχεδίαση ενός τετραγώνου.
CS
SETPOS [0 100]
SETPOS [100 100]
SETPOS [100 0]
SETPOS [0 0]
Κάθε εντολή μέσα σ’ αυτό το τετράγωνο παίρνει υπόψη του τη θέση της χελώνας μέσα στην οθόνη σαν σύνολο. Η άποψη με την οποία βλέπουμε και ζωγραφίζουμε την εικόνα είναι αυτή ενός παρατηρητή ο οποίος κάθεται πάνω από το επίπεδο κοιτάζοντας το ολόκληρο. Αυτός ο παρατηρητής βλέπει όχι μόνο τη χελώνα αλλά τις ακμές και το κέντρο της οθόνης σαν μέρος από αυτά που χρειάζεται για να ζωγραφίσει κάθε γραμμή. Αντίθετα, η γεωμετρία της χελώνας βλέπει τα πράγματα από την άποψη της ίδιας της χελώνας: κάθε γραμμή ζωγραφίζεται χωρίς να λάβουμε υπόψη μας που ακριβώς βρίσκεται η χελώνα.
Αναφέραμε τη SETPOS η οποία προσδιορίζει τη θέση της χελώνας. Υπάρχει μία ακόμα εντολή η SETH (SetHeading) η οποία καθορίζει τη διεύθυνση. Η SETH παίρνει μία είσοδο, έναν αριθμό. Το αποτέλεσμά της είναι να στρίψει η χελώνα έτσι ώστε να κοιτάζει προς τη διεύθυνση της πυξίδας που καθορίζει ο αριθμός. Το μηδέν αναπαριστά το βορρά. Η διεύθυνση μετριέται σε μοίρες από το βορρά σύμφωνα με τη φορά των δεικτών του ρολογιού. Για παράδειγμα, ανατολή = 90, δύση = 270. Η διεύθυνση της πυξίδας είναι διαφορετική από το σύστημα μέτρησης γωνιών που χρησιμοποιείται στην αναλυτική γεωμετρία, στο οποίο οι γωνίες μετριούνται αντίθετα με τη φορά του ρολογιού από την ανατολή, αντί με τη φορά του ρολογιού από το βορρά. Ουσιαστικά, με την SETH χρησιμοποιούμε πολικές συντεταγμένες.
Υπάρχουν επίσης οι operations POS και HEADING οι οποίες επιστρέφουν τιμές που περιγράφουν τη θέση και τη διεύθυνση της χελώνας αντίστοιχα. Επίσης υπάρχουν κάποιες primitive οι οποίες χρησιμοποιούνται όταν θέλουμε να αναφερθούμε μόνο σε μία από τις δύο συντεταγμένες. Όταν θέλουμε να αλλάξουμε τη x συντεταγμένη χρησιμοποιούμε την εντολή SETX. Αυτή δέχεται μια είσοδο, έναν αριθμό. Το αποτέλεσμα της είναι να μετακινηθεί η χελώνα στη συγκεκριμένη x συντεταγμένη διατηρώντας σταθερή την y. Αντίστοιχα η SETY καθορίζει την y συντεταγμένη διατηρώντας σταθερή τη x.
Αφού στη LOGO υπάρχουν το SetPosition και το SetHeading, γεννιέται το
ερώτημα ποιος ο λόγος ύπαρξης του μικρόκοσμού μας;
Τα συμπεράσματα που έβγαλε είναι ότι τα παιδιά στην εισαγωγή τους στην
καρτεσιανή γεωμετρία συναντούν θεμελιώδεις δυσκολίες οι οποίες είναι:
Η κύρια θέση του Lawler [2] για τον τρόπο μάθησης, εμπεριέχει τη δόμηση του νου ως μια διαδικασία γέννησης και αλληλεπίδρασης μικροόψεων (microviews), δηλαδή αποσπασματικών αντιλήψεων του κόσμου. Οι μικροόψεις είναι εσωτερικές γνωστικές δομές ή πλαίσια εξαρτημένα άμεσα από το περιβάλλον γύρω από την κατάσταση μέσα από την οποία γεννήθηκαν και στα οποία προβλήματα και πραγματικές εμπειρίες από την καθημερινή ζωή αφομοιώνονται. Ο Lawler εστιάζει τη μελέτη του και προσπαθεί να εξηγήσει τις σχέσεις μεταξύ των μικροόψεων και την εξέλιξή τους. Για παράδειγμα υποστηρίζει ότι οι μικροόψεις είναι συνδεδεμένες μεταξύ τους με ένα πολύπλοκο γεννεσιακό δίκτυο. Μερικές από αυτές είναι απόγονοι μιας ή και περισσοτέρων μικροόψεων, μερικές συνυπάρχουν χωρίς προφανή σχέση μεταξύ τους, αλλά με πιθανές κοινές μικροόψεις "προγόνους". Δίνει επίσης μια σχέση αλληλοκυριαρχίας μεταξύ των μικροόψεων, δηλαδή ότι υπάρχουν κυρίαρχες μικροόψεις που επηρεάζουν άμεσα τη συμπεριφορά, αλλά και μικροόψεις σε λανθάνουσα κατάσταση οι οποίες μπορούν να εκμαιευτούν μετά από παιδαγωγική ή άλλη παρέμβαση.
Ο τρόπος με τον οποίο αντιλαμβάνεται ένα παιδί την εσωγενή γεωμετρία, δηλαδή το νοητικό σχήμα που επικαλείται για να σκεφτεί για την εσωγενή γεωμετρία και το οποίο αποτελείται από διάφορες μικροόψεις, έχει τις ρίζες του σε πάρα πολύ αρχική φάση της ζωής, σε αρχικές εμπειρίες. Δεν είναι απλώς ένα νοητικό σχήμα το οποίο έχει αρχίσει να το σκέφτεται κανείς σε ηλικία 6,7 ή 8 χρόνων. Το ίδιο συμβαίνει και στην καρτεσιανή γεωμετρία. Εάν ανατρέξει κανείς προς τα πίσω και δει πάνω σε ποιες εμπειρίες βασίζεται ο τρόπος σκέψης για την καρτεσιανή γεωμετρία, τότε προχωράει σε εμπειρίες που έχει όταν είναι σε ηλικία μερικών μηνών, δηλαδή σε πολύ αρχικές εμπειρίες.
Ο Lawler υποστηρίζει ότι η βάση αυτή, η καρδιά δηλαδή των εμπειριών από τις οποίες πηγάζει η εσωγενής γεωμετρία και η καρδιά των εμπειριών από τις οποίες πηγάζει η καρτεσιανή γεωμετρία είναι πάρα πολύ διαφορετικές μεταξύ τους. Η εσωγενής γεωμετρία πηγάζει από τη βάση της κίνησης των μελών του σώματος και του σώματος του ίδιου, δηλαδή πηγάζει από τη βάση της κίνησης, ενώ η καρτεσιανή γεωμετρία πηγάζει από τη βάση της όρασης και της αντίληψης. Η καρτεσιανή γεωμετρία, δεν είναι τόσο σαφές σε τι αρχικά στάδια ανατρέχει, αλλά είναι σαφές ότι δεν ανατρέχει σε στάδια κίνησης και ανατρέχει περισσότερο σε στάδια όρασης (visually based knowledge).
Κατά την έρευνά του, θεώρησε ότι οι μικροόψεις που αντιστοιχούσαν στις εμπειρίες της κόρης του ήταν ικανές για την κατανόηση της καρτεσιανής γεωμετρίας και ότι είχαν τη δομή που φαίνεται στο ακόλουθο σχήμα.
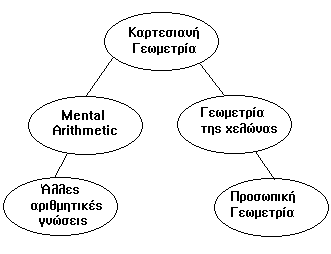
Στην πραγματικότητα, όπως απέδειξε η έρευνα, δεν αρκεί η γνώση της εσωγενούς γεωμετρίας για την κατανόηση της καρτεσιανής. Δεν επιτεύχθηκε μάλιστα καμία σύνδεση ανάμεσα στις δύο γεωμετρίες. Αυτό εξηγείται σύμφωνα με τη θεωρία μάθησης του Lawler σε σχέση με τις μικροόψεις. Κάθε καινούργια έννοια αποτελεί μια νέα μικροόψη. Όταν τα παιδιά αντιμετωπίζουν μια καινούργια έννοια, όπως η καρτεσιανή γεωμετρία, η οποία είναι έξω από τις εμπειρίες τους, τότε προσπαθούν να τη δουν μέσα από το πρίσμα κάποιας μικροόψης προγόνου. Αυτή τους παρέχει τις αντιλήψεις (δηλαδή την ανάλυση σε τμήματα και ολοκληρωμένες σχέσεις) και διαδικασίες οι οποίες χρειάζονται για την κατανόηση του προβλήματος. Η μικροόψη όμως που ανακαλείται, δεν είναι η κατάλληλη για την κατανόηση της συγκεκριμένης έννοιας, γιατί δεν υπάρχει κάποια κατάλληλη μικροόψη. Αυτή όμως είναι η πιο συγγενική από όλες τις άλλες που διαθέτει το παιδί. Είναι λοιπόν πολύ λογικό, ότι το παιδί θα συνδέσει λανθασμένα τη νέα μικροόψη με την ομάδα των μικροόψεων στην οποία ανήκει η ανακληθείσα, με αποτέλεσμα να επέλθει σύγχυση και να μην υπάρξει κατανόηση της νέας έννοιας.
Έτσι χρειάστηκε η ύπαρξη μιας άλλης μικροόψης η οποία βοηθά στην κατανόηση των καρτεσιανών συντεταγμένων.

Η απευθείας μάθηση της καρτεσιανής γεωμετρίας είναι πάλι αρκετά δύσκολη. Το Setposition, που υπάρχει στη LOGO, είναι ανακριβές μαθηματικά, διότι αναφέρεται στη χελώνα. Η χελώνα είναι μια οντότητα με θέση και διεύθυνση. Όταν της λέμε θέσε τη θέση σου κάπου, είναι σαν να μην αναφερόμαστε σε μία από τις δύο καταστάσεις της. Δεν είναι σωστό σε μια οντότητα με διπλή κατάσταση να αναφερόμαστε μόνο στη μία. Επιπλέον αν δούμε πώς λειτουργεί η SetPosition, βλέπουμε ότι παίρνει τη χελώνα από εκεί που είναι και την πάει σε μια άλλη θέση χωρίς να της αλλάζει τη διεύθυνση καθόλου. Αυτό όμως, είναι τελείως ασύνδετο νοηματικά με αυτό που κάνει η χελώνα, και με αυτό που μέχρι τώρα γνωρίζουν τα παιδιά.
Όλα αυτά έδειξαν ότι για να μάθει κανείς καρτεσιανή γεωμετρία είναι
πολύ δύσκολο όπως επίσης και η σύνδεση των εμπειριών της καρτεσιανής γεωμετρίας
με τις εμπειρίες της εσωγενούς.
Η σχεδίαση του μικρόκοσμού μας έγινε έτσι, ώστε τα παιδιά να μην συνδέουν κινήσεις καρτεσιανές, με την ίδια οντότητα με την οποία μέχρι τώρα συνδέουν κινήσεις εσωγενείς. Αν ένα παιδί έχει συνηθίσει ότι για να μετακινήσει τη χελώνα λοξώς δεξιά πρέπει πρώτα να τη στρίψει και μετά να τη μετακινήσει, δεν μπορούμε ξαφνικά να του πούμε ότι τώρα δε χρειάζεται να τη στρίψει. Έτσι ένα παιδί μπορεί με interactive και εύκολο τρόπο να φτιάχνει γεωμετρικά σχήματα στη μια γεωμετρία και να τα χρησιμοποιεί αυτά σαν οντότητες για την άλλη.
Η σύνδεση με την εσωγενή γίνεται εύκολα γιατί η μετακίνηση των σχημάτων εξαρτάται μόνο από την παρούσα θέση του σχήματος. Η επόμενη θέση βρίσκεται αν μετακινήσουμε το σχήμα από την παρούσα θέση Χ βήματα οριζόντια και Υ κατακόρυφα.
Οι δυσκολίες που παρουσιάστηκαν στα παιδιά κατά στην έρευνα του Lawler δεν παρουσιάζονται στο δικό μας μικρόκοσμο. Τα παιδιά για παράδειγμα μπερδεύτηκαν όταν μετακίνησαν τη χελώνα από την απόλυτη θέση Υ=-60 στην απόλυτη θέση Υ=-11, γιατί συμπέραναν ότι το (-) πάει τη χελώνα προς τα πάνω. Επίσης θεωρούσαν τις μεταβλητές Χ,Υ σαν state changers και όχι σαν απόλυτες συντεταγμένες. Σε μας οι μεταβλητές αυτές είναι πράγματι state changers. Είναι κάθε φορά ξεκάθαρο που θα πάει η χελώνα. Επίσης τα πρόσημα εκτελούν πάντα την ίδια λειτουργία (το + μετακινεί πάντα προς τα δεξιά ή πάνω ενώ το - προς τα αριστερά ή κάτω). Τους δίνουμε έτσι ένα σύστημα συντεταγμένων, αφού τα σημεία περιγράφονται με αριθμούς σύμφωνα με τον μαθηματικό ορισμό που έχει δοθεί προηγουμένως.
Η σύνδεση με την καρτεσιανή είναι επίσης εύκολη, γιατί το κάθε σημείο έχει συγκεκριμένο συμβολισμό και περιγράφεται με ένα ζευγάρι αριθμών. Το μόνο που πρέπει να κατανοήσουν τα παιδιά είναι ότι στις καρτεσιανές συντεταγμένες, οι αποστάσεις δεν υπολογίζονται από την παρούσα θέση αλλά υπολογίζονται με τον ίδιο ακριβώς τρόπο από κάποιο σταθερό σημείο.
Αυτό που έχουμε κάνει εμείς ουσιαστικά, είναι να δώσουμε τη δύναμη στα
παιδιά να χρησιμοποιήσουν το SetPosition. Τους δώσαμε εργαλεία με τα οποία
η χελώνα μπορεί να πάρει αντικείμενα που έχει φτιάξει με εσωγενή γεωμετρία
και να τα μετακινήσει. Δε μετακινείται πια η χελώνα, αλλά το αντικείμενο
και η νέα του θέση προσδιορίζεται με τρόπο που μοιάζει με τον τρόπο προσδιορισμού
σημείων στην καρτεσιανή γεωμετρία. Έτσι τα primitive που δώσαμε στα παιδιά,
ελπίζουμε ότι θα γεφυρώσουν αυτό το χάσμα μεταξύ εσωγενούς και καρτεσιανής
γεωμετρίας ή ότι θα μπορέσουν να δώσουν τη δυνατότητα σε δασκάλους να το
γεφυρώσουν.